图6.4典型沿岸防登陆轨条砦目标与轨条砦等本体功能型硬目标不同，桥梁桥墩、水坝大坝、高速公路等属于民用设施，但战时往往成为战场打击的重点，特别是跨海跨堑大桥、水利枢纽工程等，一旦遭到弹药攻击坍塌或溃坝，不仅抢修十分困难，更严重的是，由此引发的灾难性后果和社会恐慌甚至不亚于核打击，如图6.5所示。......
2025-09-29
典型环节频率特性分析
【摘要】：图5-7理想微分环节的幅相频率特性②理想微分环节的伯德图。图5-11积分环节的奈氏图积分环节的对数幅相频率特性。惯性环节的频率特性为对数幅频特性是上述特性可用两条渐近线来近似。二阶微分环节的频率特性为对数幅频特性为对数相频特性为其对数频率特性如图5-18所示。
一个自动控制系统一般由若干个典型环节组成，开环传递函数可表示为若干个典型环节的串联形式，即
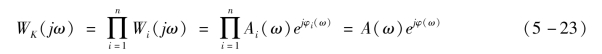
则开环系统幅相频率特性与典型环节的幅相频率特性的关系为
式（5-24）表明系统开环频率特性表现为组成开环系统的诸典型环节频率特性的合成。因此，典型环节的频率特性是研究开环系统频率特性的基础。
1.比例环节的频率特性
传递函数
频率特性
相应的对数幅频特性和相频特性为
比例环节的频率特性与频率无关，其奈氏图是正实轴上的一个点，它到原点的距离为K，如图5-5所示。当K＞1，L（ω）＞0时，比例环节的伯德图如图5-6所示。
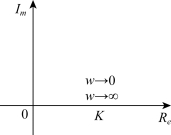
图5-5 比例环节的奈氏图
图5-6 比例环节的伯德图
2.微分环节的频率特性
（1）理想微分环节的频率特性。
①理想微分环节的幅相频率特性。
传递函数
W(s)=s
频率特性
由此得幅频特性为A（ω）=ω，相频特性为
。所以在0≪ω≪∞，理想微分环节的奈氏图为与正虚轴重合的一条直线，理想微分环节的相频特性是
的水平直线，其奈氏图如图5-7所示。
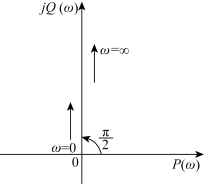
图5-7 理想微分环节的幅相频率特性
②理想微分环节的伯德图。
对数幅相频率特性为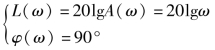
即对数幅频率特性是一条斜率为20dB/dec的直线，它与0dB线交点于ω=1点。对数相频率特性为90°的水平线，其伯德图如图5-8所示。
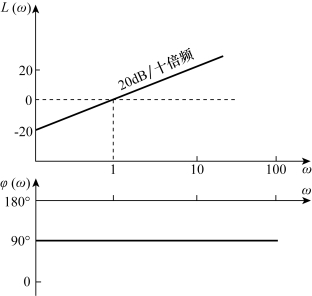
图5-8 理想微分环节的伯德图
（2）一阶微分环节的频率特性。
①一阶微分环节的幅相频率特性。
传递函数
W(s)=Ts+1
频率特性
由此得幅频特性为
相频特性为φ（ω）=arctanωT。可得到当ω从0变到∞时，奈氏曲线的几个特殊点如下。
一阶微分环节的奈氏图是复平面第一象限中一条通过（1，j0）点，并与虚轴平行的直线，如图5-9所示。
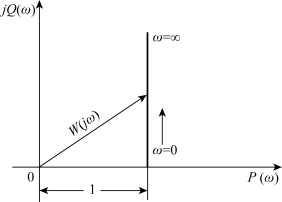
图5-9 一阶微分环节的奈氏图
②一阶微分环节的伯德图。
一阶微分环节的频率特性为
对数幅频特性是
对数相频特性是
一阶微分环节的对数幅频特性对数相频特性如图5-10所示。
图5-10 一阶微分环节的伯德图
3.积分环节的频率特性
（1）积分环节的幅相频率特性
传递函数
频率特性
由此得幅频特性为
，相频特性为
可见，积分环节的奈氏曲线是一条与负虚轴重合的曲线，如图5-11所示。
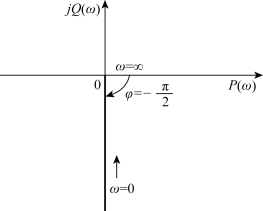
图5-11 积分环节的奈氏图
（2）积分环节的对数幅相频率特性。
积分环节的频率特性为
其对数幅频特性是
对数相频特性是
由式（5-27）知，L（ω）与ω的关系是一条对数曲线，而L（ω）与lgω成正比关系。在半对数坐标上，对数幅频特性是一条斜率为-20dB/dec的直线。-20dB/dec表示ω每增加十倍频程L（ω）减小20dB。其伯德图如图5-12所示。
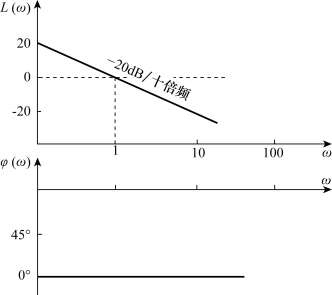
图5-12 积分环节的伯德图
（3）多个积分环节或者多个理想微分环节串联的对数幅相频率特性。
①若有多个积分环节串联，即频率特性为
其对数幅频特性是
对数相频特性是
此时，对数幅频特性是斜率为-20ndB/dec的直线，相频特性是
的水平直线。当n=2时系统的多个积分环节的伯德图如图5-13所示。
②有多个理想微分环节串联，频率特性为
对数幅频特性是
对数相频特性是
图5-13同时给出了n=2时系统的多个理想微分环节串联的伯德图。
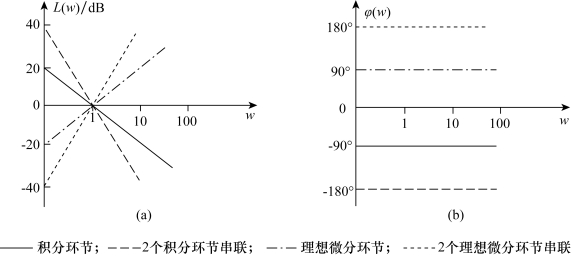
图5-13 积分、微分环节的伯德图
4.惯性环节的频率特性
（1）惯性环节的幅相频率特性。
传递函数 
频率特性 
(https://www.chuimin.cn)
式中，幅频特性为
相频特性为φ（ω）=-arctanωT。可得到当ω从0变到∞时，奈氏曲线的几个特殊点如下。
绘制幅相频率特性曲线，即奈氏图，如图5-14所示。它是一半圆，证明如下：
图5-14 惯性环节的奈氏图
式中，
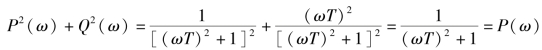
化简得到
这是一个圆心在
、半径等于
的圆。当ω从0变到∞时，φ（ω）为负，所以惯性环节的幅相频率特性曲线为半圆。
（2）惯性环节的伯德图。
惯性环节的频率特性为
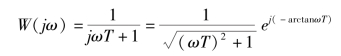
对数幅频特性是
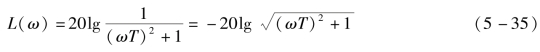
上述特性可用两条渐近线来近似。
时，L（ω）=-20lg1=0dB，即0dB的水平线。
时，L（ω）=-20lgωT是一条斜率为-20dB/dec的直线。
时，是两条渐近线的交点角频率，称为交接频率或转折频率。在绘制惯性环节对数频率特性时，交接频率是一个重要参数。对数幅频特性可用渐近线特性代替实际曲线，但是，会在交接频率附近存在误差。
最大误差出现在
处，由式（5-35）可求得
所以对于此类环节，采用渐近线近似实际曲线引起的误差不超过3dB，但大大简化了对数幅频特性的绘制。
对数相频特性是
为了绘制相频特性，确定以下几个点就可以了。
采用描点法可绘制出相频特性曲线，如图5-15所示。
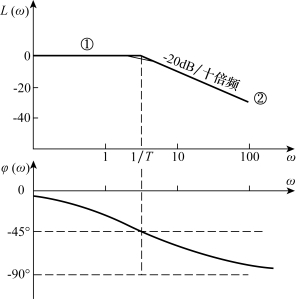
图5-15 惯性环节的伯德图
5.振荡环节的频率特性
（1）振荡环节的幅相频率特性曲线。
传递函数为
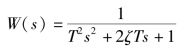
频率特性为
式中，幅频特性为
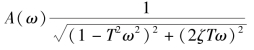
相频特性为
以ζ为参变量，计算不同频率ω时的幅值和相角，其中几个特征点如下。
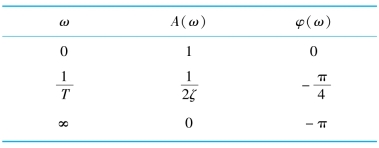
画出ω由0变∞到时的矢量端点的轨迹，即可得到振荡环节的幅相频率特性，如图5-16所示。
图5-16 振荡环节的奈氏图
（2）振荡环节或二阶微分环节[T2（jω）2+2ζTjω+1]±1的伯德图。
①振荡环节的伯德图。
振荡环节的频率特性为
对数幅频特性为
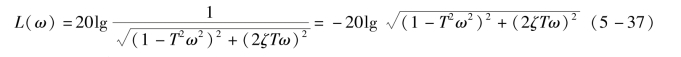
上述特性可用两条渐近线来近似：
时，L（ω）=-20LG1=0（dB），即0dB的水平线。
ω≫时，L（ω）=-40lgωT，是一条斜率为-40dB/dec的直线。
这两条渐近线相交处的频率就是交接频率
。在
附近，渐近线与实际曲线之间存在较大误差。
时，由渐近线特性知
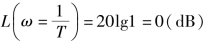
而由准确特性知
只有在ζ=0.5时，两者相等。不同ζ时的精确曲线如图5-17所示。所以，对于振荡环节以渐近线代替实际对数频率特性时，要特别注意，如果ζ在0.4～0.7范围内，则误差不大，超出这个范围要考虑修正误差。且由图5-17可知，在0＜ζ＜0.707时，对数幅频特性将出现谐振峰值Mp，其大小与阻尼比有关。根据求极值的方法，由幅频特性A（ω）对频率ω求导数，并令其等于零，可求得谐振角频率ωP和谐振峰值MP。
对数相频特性为
可采用描点法绘制。不同ζ下的φ（ω）曲线见图5-17。
图5-17 振荡环节的伯德图
②二阶微分环节的伯德图。
二阶微分环节的频率特性为
对数幅频特性为
对数相频特性为
其对数频率特性如图5-18所示。二阶微分环节的对数幅频特性L（ω）与振荡环节的L（ω）关于0分贝线对称，对数相频特性φ（ω）与振荡环节关于0度线对称。
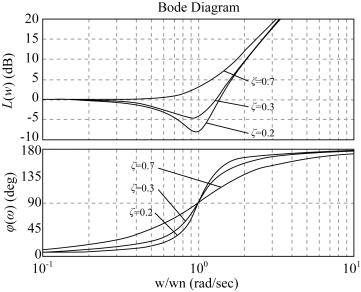
图5-18 二阶微分环节的伯德图
6.时滞环节的频率特性
（1）时滞环节的幅相频率特性。
传递函数为 W（s）=e-τs
频率特性为 W（jω）=e-jωτ=A（ω）ejφ（ω）
式中，A（ω）=1，φ（ω）=-ωτ。故时滞环节的幅相频率特性是一个以原点为圆心、半径为1的圆，如图5-19所示。
（2）时滞环节的伯德图。
时滞环节的对数幅频特性为 L（ω）=20lg1=0
时滞环节的对数相频特性为 φ（ω）=-τω
其伯德图如图5-20所示。
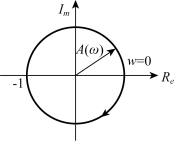
图5-19 时滞环节的奈氏图
图5-20 时滞环节的伯德图
相关文章
- 详细阅读
-
典型装甲目标的特性分析详细阅读
图4.1披挂ERA的主战坦克图4.2ERA抗弹防护原理目前，俄罗斯、美国、德国、英国、法国、以色列、中国等国均已发展了系列化ERA，其中又以俄罗斯“接触/K”系列ERA最具代表性。图4.6美国“福特”级航母结构布局现代大中型......
2025-09-29
-
典型流域植被与侵蚀状态图分析详细阅读
以上讨论了长江上游小江流域和黄土高原甘肃安家沟流域的植被—侵蚀状态图，可以分别代表气候、土壤、地形相近的金沙江干热河谷地区和黄土高原西部地区的植被—侵蚀状态图。王家沟流域的植被侵蚀动力学参数值由式给出，作出状态图如图7-21 。治理初期植被侵蚀状态位于A 区，治理的目标是将其移入C 区。......
2025-09-29
-
串联谐振电路的频率特性分析详细阅读
即图5.2串谐电路的频率特性曲线图图5.2中给出了阻抗和电抗随频率变化的关系曲线。此例说明，当电压值相同、频率不同的两个信号通过串联谐振电路时，电路的选择性使两信号在回路中产生的电流相差10倍以上。......
2025-09-29
-
典型风力发电系统及其控制方案分析详细阅读
目前，风力发电系统的主流为变速恒频发电系统。在变速恒频风力发电系统中，绕线转子双馈异步电动机和永磁同步电动机是迄今使用最广的两类风力发电机。双馈感应风力发电系统中的网侧变流器主要用于实现直流母线电压的稳定控制，完成转子侧与电网间有功功率和无功功率的交换而转子侧变流器用于双馈发电机的转子励磁控制，实现最大风能的跟踪。......
2025-09-29
-
典型河段岸滩侧蚀对航道的影响分析详细阅读
图6.2-8清水冲刷后长江中游太平口水道洲滩边界变化由腊林洲边滩有、无侧蚀情况下太平口水道3.5m航深线的预测对比结果可看出，腊林洲边滩的守护措施，对于“南槽-北汊”航道格局的稳定具有重要作用。因此，以已建航道整治工程为依托，进一步实施航道整治工程措施，守护较为有利的洲滩格局，防止腊林洲边滩侧蚀后退，同时适当恢复腊林洲低滩的滩体，是强化和稳定该水道“南槽-北汊”航道格局的基础。......
2025-09-29
- 详细阅读
-
典型RAM芯片介绍详细阅读
水平放置的MFD顶部有7个PDP，两侧各有6个PDP；竖直放置的地图显示器顶部有6个PDP，两侧各有10个PDP。所有的MFD都采用触摸屏，也可以通过光笔、键盘、手柄上的拇指光标控制器进行交互。车长主要通过MFD完成任务，也可通过字母/数字键盘、可编程显示按钮、拇指光标控制器和4个方向按键与坦克进行交互。......
2025-09-29
相关推荐