频率特性图示法有哪些？

2025-09-29 理论教育版权反馈

【摘要】：在曲线中，频率ω为参变量，一般用小箭头表示ω增大时幅相频率特性曲线的变化方向。图5-3系统的奈氏图2.对数频率特性曲线对数频率特性是将频率特性表示在半对数坐标中。对系统的频率特性的表示式两边取对数，得这就是对数频率特性的表达式。对数幅相频率特性曲线又称为尼柯尔斯曲线，简称尼氏图。

1.幅相频率特性曲线（又称奈氏图、极坐标图）

系统的频率特性为

式中，A（ω）是频率特性的模，即幅频特性；φ（ω）是频率特性的辐角或相移，即相频特性。对于某一频率ω下的W（jω）总可以在复平面上找到一个向量与之对应，向量的长度为A（ω），与实轴的夹角为φ（ω），不同ω下的向量的端点在复平面上扫过的轨迹即为该系统的幅相频率特性曲线，如图5-3（a）所示。

式（5-18）也可以表示为代数形式，即直角坐标形式：

式中，P（ω）是频率特性的实部，称为实频特性；Q（ω）是频率特性的虚部，称为虚频特性，如图5-3（b）所示。

系统幅频特性、相频特性与实频特性、虚频特性存在如下关系。

pagenumber_ebook=114,pagenumber_book=103

定义新的复平面，将极坐标与直角坐标重合，如图5-3（c）所示，取极点为直角坐标的原点，取极坐标轴为直角坐标的实轴。

在上述定义的复平面上，当频率ω由-∞变化到+∞时，W（jω）的矢量终端将在复平面上绘出一条曲线，称为系统（或环节）的幅相频率特性曲线，或叫极坐标图，或叫奈奎斯特曲线，简称奈氏图。由于幅频特性为ω的偶函数、相频特性为ω的奇函数，ω从0变到+∞和ω从-∞变到0的幅相频率特性曲线关于实轴对称，因此一般只绘出ω从0变到+∞的幅相频率特性曲线。在曲线中，频率ω为参变量，一般用小箭头表示ω增大时幅相频率特性曲线的变化方向。

pagenumber_ebook=114,pagenumber_book=103

图5-3　系统的奈氏图

2.对数频率特性曲线（又称伯德图）(https://www.chuimin.cn)

对数频率特性是将频率特性表示在半对数坐标中。

对系统的频率特性的表示式（5-18）两边取对数，得

这就是对数频率特性的表达式。习惯上一般不考虑系数0.434，而只用相角位移本身。

通常将频率特性幅值扩大20倍，单位用分贝（dB）表示，其对数幅频特性表达式为

对数频率特性的坐标如图5-4所示，图中横坐标轴为角频率ω，采用对数比例尺（或称对数刻度）。对数幅频特性的纵坐标是按A（ω）的对数值20lgA（ω）=L（ω）进行线性分度的，标注的也是20lgA（ω）的值，该坐标是普通坐标，单位为分贝（dB）。这种坐标的特点是，如果在横轴上取两点满足，则该两点的距离为，这就是说频率每变化10倍，在横坐标轴上线段长度均为一个单位，叫作一个“十倍频”或“十倍频程”，以“dec”表示。图中纵坐标为L（ω）称为幅频增益。A（ω）每变化十倍，L（ω）变化20dB，可用线性刻度表示。这样可以展宽频带，并且在半对数坐标系中所有典型环节的对数幅频特性都可以用分段直线来近似表示。对数相频特性的横坐标与幅频特性的横坐标相同，其纵坐标表示相角位移φ（ω），单位为“度”（“°”）或“弧度”（“rad”），采用线性刻度。由此，构成的坐标系统称为半对数坐标系。分别将对数幅频特性和对数相频特性绘制在两个半对数坐标系中，称为对数频率特性图，常称为伯德图（Bode图）。

对数频率特性ω采用对数分度实现了横坐标的非线性压缩，便于在较大频率范围内反映频率特性的变化情况。对数幅频特性采用20lgA（ω）作为纵坐标，它将幅值的乘除运算化为加减运算，可以简化曲线的绘制过程。这样绘图既简单、方便，又能够直观地显示出系统中每个环节的作用，便于对系统进行分析与校正，因此伯德图在频率分析法中应用最多。

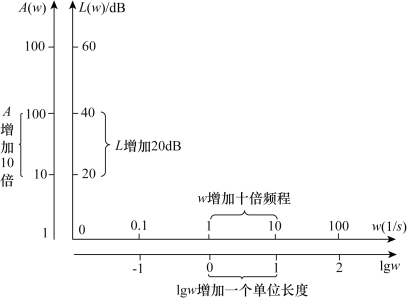
pagenumber_ebook=115,pagenumber_book=104

图5-4　对数频率特性的坐标（半对数坐标）

3.对数幅相频率特性曲线（又称尼氏图）

对数幅相频率特性曲线是将对数幅频率特性和对数相频率特性两条曲线合并成一条曲线。对数幅相图的横坐标为相角φ（ω），纵坐标为对数幅值L（ω）=20lgA（ω），皆为线性分度。对数幅相频率特性曲线又称为尼柯尔斯曲线，简称尼氏图。

对数幅相频率特性可以方便地从伯德图中求得，频率ω是参变量。

频率特性图示法有哪些？

相关推荐