DOCTYPE html ＞部分、＜html ＞标记、头部＜head ＞标记、主体＜body ＞标记三大部分，头部描述浏览器所需的信息，主体包含所要说明的具体内容，声明部分告知浏览器文档使用HTML 规范，如下所示：3.HTML52014 年10 月29 日，万维网联盟宣布HTML5 标准规范最终制定完成，并公开发布。设计HTML5 的目的是在移动设备上支持多媒体。......
2023-11-25
无线电频率特性基础知识
【摘要】：下面以如图5-1所示的RC滤波网络为例，建立频率特性的基本概念。该比值给出了在不同频率下电路传递正弦信号的性能。u0=UA(ω)sin由于RC滤波电路的传递函数为对比式（5-4）和式（5-5）就会发现，该电路的频率特性W（jω）和传递函数W的表达式形式是相同的。传递函数的复变量s用jω代替时，传递函数就转变为频率特性函数。
一个稳定的线性控制系统，在正弦信号的作用下，稳态时输出仍然是一个同频率的正弦信号，只是输出信号的幅值和相位一般不同于输入。它们都是输入信号频率的函数。
下面以如图5-1所示的RC滤波网络为例，建立频率特性的基本概念。
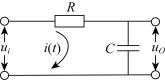
图5-1 RC滤波电路
设输入信号为正弦交流电压 ui=Usin（ωt+φ）
ui对应的电压相量为
如果系统为线性定常系统，则输出量uo也必为同频率的正弦信号，uo对应的电压相量为
RC滤波网络总复阻抗为 
于是，其输入、输出电压相量的比值为
式（5-3）表示把一个频率为ω的正弦信号作用于电路或系统时，在稳态条件下电路或系统的输出量和输入量的比。这个比值是复数，是随频率而变化的，频率不同，比值的幅值大小和相位移动不同。该比值给出了在不同频率下电路传递正弦信号的性能。我们把这个比值叫作电路的频率特性或频率响应，常用W（jω）表示，可以写成
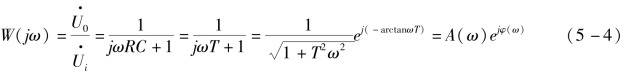
式中，T=RC，
，φ（ω）=-arctanTω。A（ω）、φ（ω）分别反映RC网络在正弦信号作用下，稳态输出与输入的幅值之比和相位之差，它们都是输入正弦信号频率ω的函数，分别称为电路或系统的幅频特性和相频特性。
这样，RC网络在受到谐波信号输入作用后，其输出量的稳态值为
写成瞬时值为 即电路或系统在受到谐波信号输入作用后，输出的稳态值等于电路或系统的频率特性函数和输入量的乘积。
u0=UA(ω)sin(ωt+φ(ω))
由于RC滤波电路的传递函数为
对比式（5-4）和式（5-5）就会发现，该电路的频率特性W（jω）和传递函数W（s）的表达式形式是相同的。只要传递函数W（s）中的算子s是用jω代替，就可以得到频率特性W（jω）。
在一般情况下，系统的传递函数可写成
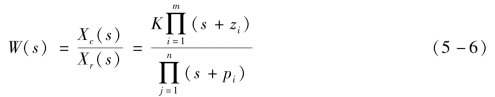
设输入正弦信号xr（t）=Xrsinωt，则输出的拉氏变换为
如果讨论的系统是稳定的，则式（5-6）中的-pi均有负实部。
如果式（5-6）的全部极点均不相同，则式（5-7）的展开式为
式中，A01，A02，A1，…，An为待定系数。
对式（5-8）两边分别求拉氏反变换，得到
对于稳定的系统，由于-pi（i=1，2，…，n）有负实部，因此，当t趋于无穷大时，各指数项e-pit（i=1，…，n）均衰减到零。也就是说，达到稳态时，输出信号xc（t）中的暂态分量将消失。这时，其稳态分量仅由式（5-9）的第一和第二项决定，即
如果（5-6）包含h重极点sj，则xc（t）中包含tie-sit（i=1，2，…，j-1）等项。对于稳定的系统，由于-sj具有负实部，所以当t趋于无穷大时，tie-sit各项都趋于零，故仍然能够得到式（5-10）的结果。
式（5-10）的系数确定如下：
式中，W（jω）是一个复数，可以表示为
在所讨论的系统响应问题中，式（5-13）具有如下特点：
将式（5-11）、式（5-12）、式（5-13）和式（5-14）代入式（5-10），得
由式（5-15）可见，在正弦信号的输入作用下，线性系统的稳态输出是同频率的正弦信号，且与输入信号都是ω的函数，对所有角频率（ω=0→+∞），系统的输入、输出的对应关系可用系统的稳态输出与输入正弦函数之幅值比A（ω）和其相位差φ（ω）随ω变化的特性来表示，这就是系统的频率特性。当输入信号与输出信号为非周期函数时，频率特性是输出信号的傅氏变换与输入信号的傅氏变换之比，即
可见，系统的频率特性可以由该系统的传递函数求得，即以jω代替s：
综上所述，系统的频率特性定义为线性系统或环节在零初始条件下稳态输出正弦信号与输入正弦信号对应的相量之比。它反映系统在不同频率正弦信号输入作用下，输出正弦信号将产生不同的幅值变化和相位移动的特性。传递函数的复变量s用jω代替时，传递函数就转变为频率特性函数。
有关自动控制原理的文章
- 详细阅读
-
典型环节频率特性分析详细阅读
图5-7理想微分环节的幅相频率特性②理想微分环节的伯德图。图5-11积分环节的奈氏图积分环节的对数幅相频率特性。惯性环节的频率特性为对数幅频特性是上述特性可用两条渐近线来近似。二阶微分环节的频率特性为对数幅频特性为对数相频特性为其对数频率特性如图5-18所示。......
2023-06-28
-
无线电的黄金时代：根斯巴克的业余无线电先驱详细阅读
诚然，从卢森堡移民而来的企业家根斯巴克大力提倡无线电，这里面有他的既得利益。他是业余无线电的先驱，创立了电气进口公司，又称Telimco 。根斯巴克认为，无线电是“将来白手起家的人的最好的基础”。马可尼无线电报公司很快成为向商船和军舰提供无线电设备和服务的主要供应商。这一切固然使参与者兴奋激动，但几千台无线电报机一拥而上，完全放任自流的坏处也随即显现出来。......
2023-11-19
-
直流故障的频率特性分析详细阅读
从以上分析可以看到，为了抑制电网发生直流闭锁故障后的频率超标问题，需要考虑最恶劣的运行方式，特别是小负荷运行方式。此时，系统的转动惯量较少，频率变化比较敏感，抵御能量的不平衡能力较差。图6.11输电网直流双极闭锁，冬季小负荷下，风电接入容量分别为2 000 MW、6 000 MW、8 000 MW、10 000 MW条件下，电网的频率特性曲线......
2023-06-29
-
学习汉族民歌：音乐基础知识详细阅读
这首民歌的歌词共有17段，讲述的是兰花花凄美的爱情故事，歌曲内容与民间传说大体相同。陕北民歌中的甩腔在信天游中较为多见，一般运用在首句的尾音。......
2023-10-26
- 详细阅读
-
频率特性基本关系探析详细阅读
图5-48频域与时域的反比特性这种关系也可表现在时域描述中，但平移方向是相反的。图5-49对数幅频特性斜率与相位的关系根据波特定理，幅值穿越频率ωc的对数幅频特性的斜率对系统相位裕量影响最大，而远离ωc的特性斜率影响较小。......
2023-06-28
-
系统开环对数频率特性分析详细阅读
开环传递函数可分解为基本环节的串联形式，如式和式，在此基础上，系统的开环对数幅频特性和对数相频特性分别为表明开环系统对数频率特性表现为诸基本环节对数频率特性叠加这一简单的形式。在ωωmin频段，系统开环对数幅频特性渐近线表现为分段折线。系统开环对数幅频渐近特性曲线如图5-29所示。图5-29系统对数频率特性注意到此系统中有一个一阶微分环节，将使相角有正的位移偏向。......
2023-06-28
相关推荐