本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出线性控制系统根轨迹分析中常用的MATLAB命令。
（1）绘制根轨迹指令。
rlocus（num，den）：绘制指定系统的根轨迹。
rlocus（num，den，K）：绘制指定系统的根轨迹。K为给定增益向量。
[p，z]=pzmap（num，den）：绘制零极点图。
（2）根轨迹分析指令。
[K，POLES]=rlocfind（G）：交互式地选取根轨迹增益。产生一个十字光标，用此光标在根轨迹上单击一个极点，同时给出该增益所有对应极点值。
[K，POLES]=rlocfind（G，P）：返回P所对应根轨迹增益K，及K所对应的全部极点值。
例4-7 系统开环传递函数为如下式，绘制该系统的根轨迹图。
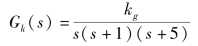
解：根轨迹作图程序如下：
该系统的根轨迹如图4-18所示。
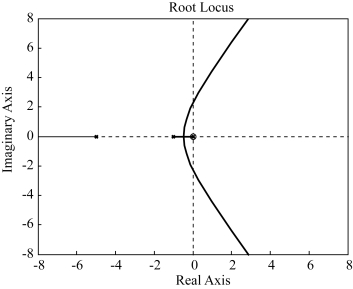
图4-18 例4-7系统的根轨迹图
由图4-18可知，系统的极点为p1=0，p2=-1，p3=-5；根轨迹有3条，都以极点起始，终止于无穷远。
例4-8 给定单输入—单输出系统（SISO）的传递函数：
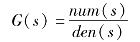
分子多项式系数向量num和分母多项式系数向量den，在s平面作零极点图。
函数格式1：计算零极点并作图。
函数格式2：返回变量格式。计算所得的零极点向量p，z返回至matlab命令窗口，不作图。
例4-9 传递函数如下式，绘制该传递函数的零极点图。
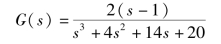
解：程序为：num=[2，-2]，den=[1，4，14，20]，pzmap（num，den）。
零极点图如图4-19所示。
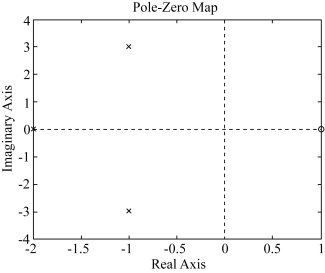
图4-19 例4-9传递函数的零极点图
例4-10 若单位负反馈控制系统的开环传递函数为
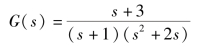
绘制系统的根轨迹，并据根轨迹判定系统的稳定性。
解：运行程序如下。
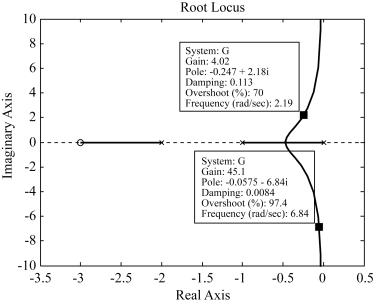
图4-20 例4-10传递函数的零极点图
分析：由根轨迹图4-20，对于任意的Kg，根轨迹均在s左半平面。系统都是稳定的。
可取增益Kg=4和Kg=45并通过时域分析验证。图4-21分别给出了Kg=4时和Kg=45时系统的单位阶跃响应曲线。可见，在Kg=45时因为极点距虚轴很近，振荡已经很大。
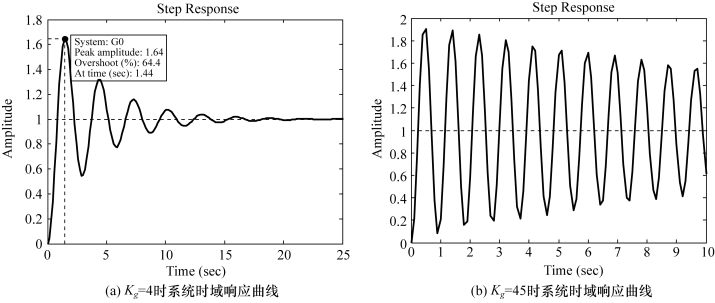
图4-21
例4-11 若单位负反馈控制系统的开环传递函数为
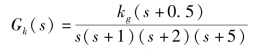
绘制系统的根轨迹，确定当系统稳定时，参数的取值范围。
解：运行程序如下。
根轨迹图如图4-22所示。
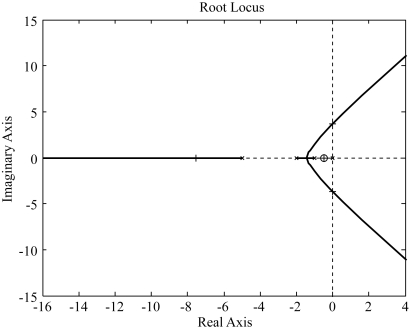
图4-22 例4-11传递函数的根轨迹图
利用鼠标在根轨迹上选择K点：
根轨迹图4-22，结合临界稳定值可知，系统稳定时，临界稳定时的阶跃响应曲线如图4-23所示。
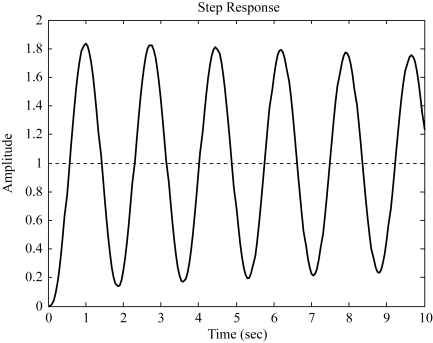
图4-23 例4-11系统的阶跃响应
有关自动控制原理的文章
例4-6 某负反馈系统的开环传递函数，试作系统K*变动的闭环根轨迹，并进行动态分析。渐近线：分离点坐标sd：解得：sd1=0.46，sd2=-0.79+j2.16，sd3=-0.79-j2.16，sd4=-2.22。其中，sd1和sd4为根轨迹上的分离点，将sd2、sd3舍去。系统闭环特征方程为s(s-1)+K*(s+1)=0展开，整理得s4+3s3+12s2+s+K*=0令s=jω，则有解之，得ω1,2=±1.56ω3,4=±2.56由图4-17可以看出，当K*在23.3～35.7范围内，根轨迹位于s平面左侧，闭环系统是稳定的。K*在其他范围内取值，系统均不稳定。图4-17例4-6根轨迹图......
2023-06-28
下面以如图4-1所示的二价控制系统为例，说明什么是根轨迹。表4-1随着K取值变化的s1、s2的各点坐标值图4-2根轨迹图闭环系统特征方程的根，就是系统闭环传递函数的极点。根轨迹法具有直观的特点，利用系统的根轨迹可以分析结构和参数已知的闭环系统的稳定性和瞬态响应特性。......
2023-06-28
系统的闭环特征方程为取其模值得模值方程为取其相角得相角方程为模值方程和相角方程成为根轨迹方程，从这两个方程可以看出，模值方程与增益K*有关，而相角方程与增益K*无关。所以，相角方程式决定闭环根轨迹的充分必要条件，而模值方程主要用来确定根轨迹上各点对应的开环增益值。，sn为闭环极点，在根轨迹图中用Δ表示。......
2023-06-28
规则2：根轨迹的对称性。会合角是指根轨迹进入会合点处的切线与实轴正方向的夹角。规则8：根轨迹的起始角与终止角。终止角的计算公式如下：如图4-7所示，z1点的终止角计算式为图4-7根轨迹的终止角规则9：根轨迹与虚轴交点及临界根轨迹增益。设根轨迹上的一点sk确定，则可根据模值方程求出对应的K*和K。例4-3 已知单位负反馈系统的开环传递函数，试绘制K从0→∞变化时闭环的根轨迹图。......
2023-06-28
MATLAB信号处理箱覆盖了经典信号处理理论的大多数内容，是一个非常优秀的算法研究和辅助设计工具。Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。MATLAB画出的图像如图1-9所示。......
2023-06-23
本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出时域分析时常用的MATLAB命令。例3-11 已知闭环系统传递函数为试用MATLAB判断系统的稳定性。图3-30例3-12系统的阶跃响应曲线图3-31例3-12系统的脉冲响应曲线例3-13 已知单位负反馈控制系统的开环传递函数为，试用MATLAB计算系统在单位阶跃信号作用下的tr、tp、ts、σ%。......
2023-06-28
本节主要讨论MATLAB在描述函数法分析中的应用。振荡频率与振荡幅值如图7-42可知分别为（方法二）线性部分的频率特性为具有死区继电特性的描述函数及相对描述函数：在程序文件方式下执行以下MATLAB程序OK1.m，在同一复平面上绘制非线性特性的相对负倒描述函数与线性部分的Nyquist曲线。非线性系统自激振荡时有运行以下程序，由，求自激振荡的振幅X。......
2023-06-28
）总之，解释为主语在后的主谓句，我们就要费很大力；就要碰到难以克服的困难；要是说它们是无主句，这些困难就不会有了。但是如果这样处理，就很有问题，因为与无主句有两点重要的不同。需要主语，证明这类句子不是无主句；前面有隐藏的主语，也证明这类句子不宜于算作无主句。......
2023-08-07
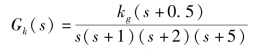
相关推荐