首页理论教育系统阶跃响应根轨迹分析

系统阶跃响应根轨迹分析

2023-06-28 理论教育版权反馈

【摘要】：例4-6 某负反馈系统的开环传递函数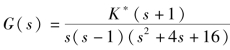，试作系统K*变动的闭环根轨迹，并进行动态分析。渐近线：分离点坐标sd：解得：sd1=0.46，sd2=-0.79+j2.16，sd3=-0.79-j2.16，sd4=-2.22。其中，sd1和sd4为根轨迹上的分离点，将sd2、sd3舍去。系统闭环特征方程为s(s-1)+K*(s+1)=0展开，整理得s4+3s3+12s2+s+K*=0令s=jω，则有解之，得ω1,2=±1.56ω3,4=±2.56由图4-17可以看出，当K*在23.3～35.7范围内，根轨迹位于s平面左侧，闭环系统是稳定的。K*在其他范围内取值，系统均不稳定。图4-17例4-6根轨迹图

例4-6 某负反馈系统的开环传递函数 pagenumber_ebook=102,pagenumber_book=91 ，试作系统K*（由0→∞）变动的闭环根轨迹，并进行动态分析。

解：（1）开环极点：p1=0，p2=1，

开环零点：z1=-1。

（2）实轴上根轨迹区段（0，1），（-∞，-1）。

（3）渐近线：

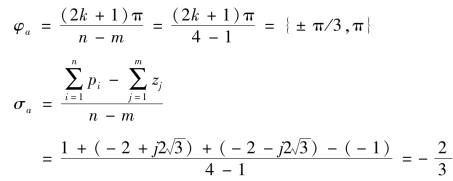
pagenumber_ebook=102,pagenumber_book=91

（4）分离点坐标sd：

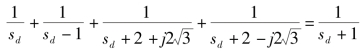
pagenumber_ebook=102,pagenumber_book=91

解得：sd1=0.46，sd2=-0.79+j2.16，sd3=-0.79-j2.16，sd4=-2.22。其中，sd1和sd4为根轨迹上的分离点，将sd2、sd3舍去。

（5）实轴上的分离角与会合角：±90°和0°、180°。

（6）起始角：

θp3=(2k+1)π+∠(p3-z1)-∠(p3-p1)-∠(p3-p2)-∠(p3-p4)

=(2k+1)π+106°-120°-130.5°-90°

=-54.5°θp4

=+54.5°

（7）与虚轴交点坐标及临界增益。系统闭环特征方程为

s(s-1)(s2+4s+16)+K*(s+1)=0

展开，整理得

s4+3s3+12s2+(K*-16)s+K*=0

令s=jω，则有

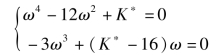
pagenumber_ebook=103,pagenumber_book=92

解之，得

ω1,2=±1.56(K*=23.3)

ω3,4=±2.56(K*=35.7)

由图4-17可以看出，当K*在23.3～35.7范围内，根轨迹位于s平面左侧，闭环系统是稳定的。K*在其他范围内取值，系统均不稳定。

pagenumber_ebook=103,pagenumber_book=92

图4-17　例4-6根轨迹图