根轨迹定义及其作用

2023-06-28 理论教育版权反馈

【摘要】：下面以如图4-1所示的二价控制系统为例，说明什么是根轨迹。表4-1随着K取值变化的s1、s2的各点坐标值图4-2根轨迹图闭环系统特征方程的根，就是系统闭环传递函数的极点。根轨迹法具有直观的特点，利用系统的根轨迹可以分析结构和参数已知的闭环系统的稳定性和瞬态响应特性。

根轨迹是一种图解方法，是指闭环系统特征方程的根（即闭环极点）随开环系统某一参数由零变化到无穷大时在s平面上的变化轨迹。

常规根轨迹：当变化的参数为开环增益时所对应的根轨迹。

广义根轨迹：当变化的参数为开环传递函数中其他参数时所对应的根轨迹。

系统传递函数的分子多项式和分母多项式经因式分解后可写成如下形式：

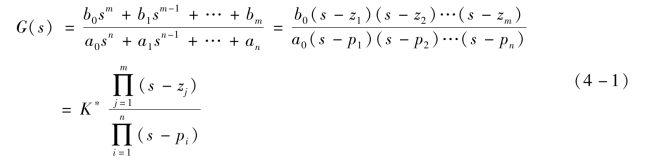
pagenumber_ebook=86,pagenumber_book=75

式中，zj（j=1，2，…，m）是分子多项式的零点，称为传递函数的零点。Pi（i=1，2，…，n）是分母多项式的零点，称为传递函数的极点。零点和极点可以是实数，也可以是复数。系数k*=b0/a0称为根轨迹增益。下面以如图4-1所示的二价控制系统为例，说明什么是根轨迹。

该系统的开环传递函数为

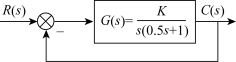
pagenumber_ebook=87,pagenumber_book=76

图4-1　控制系统框图

其闭环传递函数为

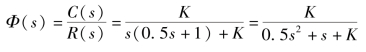
pagenumber_ebook=87,pagenumber_book=76

则闭环特征方程为

0.5s2+s+K=0

解之得闭环特征根表达式为

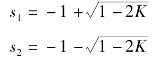
pagenumber_ebook=87,pagenumber_book=76

令K从0到+∞增大，则K和系统闭环极点的s1、s2关系如下。

（1）当K=0时，s1=0、s2=-2，此时闭环极点就是开环极点。

（2）当0＜K＜0.5时，s1、s2均为负实数，且位于负实轴的（-2，0）一段上。

（3）当K=0.5时，s1=s2=-1，两个负实数闭环极点重合在一起。

（4）当1＜K＜∞时，，两个闭环极点变为一对共轭复数极点，s1、s2的实部不随K变化，其位于过（-1，0）点并且平行于虚轴的直线上。

（5）当K=∞时，s1=-1+j∞，s2=-1-j∞，此时s1、s2将趋于无穷远处。

取K从0到∞增大的不同值代入s1、s2表达式得s1、s2的各点坐标值，如表4-1所示。

综合上述情况，当K从0到+∞增大时，如图4-1所示控制系统的闭环极点在s平面上的移动轨迹如图4-2所示。该轨迹是连续变化的，并且有两条分支，终点均在无穷远处。这就是将表格中各点坐标绘制成的该系统的根轨迹图。

表4-1　随着K取值变化的s1、s2的各点坐标值

pagenumber_ebook=87,pagenumber_book=76

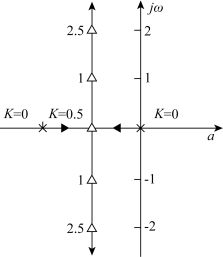
pagenumber_ebook=88,pagenumber_book=77

图4-2　根轨迹图

闭环系统特征方程的根，就是系统闭环传递函数的极点。因此，从已知的系统开环零、极点位置和某一参数变化来求取系统闭环极点的分布，实际上就是解决系统闭环特征方程的求根问题。当系统阶次大于4时，求解过程非常复杂。1948年，由伊文斯（W.R.Evans）提出了一种求闭环系统特征方程根的简单方法，并且在控制系统的分析与设计中得到了广泛应用。这一方法不直接求解闭环系统的特征方程，而是用作图的方法表示特征方程的根与系统某一参数的全部数值关系，只需依据开环传递函数便可绘制系统的根轨迹图。根轨迹法具有直观的特点，利用系统的根轨迹可以分析结构和参数已知的闭环系统的稳定性和瞬态响应特性。在设计现行控制系统时，根据对系统性能指标的要求可调整参数以及系统开环零、极点的位置，根轨迹法可以用于控制系统的分析与综合。

根轨迹定义及其作用

相关推荐