若k是按系统对稳态误差的要求选取的，则此项自然满足，可免去。需要校验的稳态误差可能包括：1.输入信号引起的误差e1）位置信号x=x0引起的误差eP。3）反馈传感器精度所引起的误差ε3不因k的改变而减少，故必须使反馈传感器有较高的精度。......
2023-06-15
消除稳态误差的有效措施
【摘要】：为了减小或消除系统稳态误差，可以增加积分环节的个数，或增大开环增益。在保证系统稳定的前提下，为实现提高稳态精度，可采用复合控制的措施来减小稳态误差。显然，增加扰动补偿的复合控制，只要选取适当的补偿环节，可以减小甚至消除扰动信号引起的稳态误差，且扰动补偿复合控制也不改变原系统的稳定性。
系统稳态误差除与输入外部作用有关之外，主要是由系统中积分环节的个数、开环增益来确定的。为了减小或消除系统稳态误差，可以增加积分环节的个数，或增大开环增益。但一般系统的积分环节不能超过两个，开环增益也不能随意增大，否则将使系统动态性能变坏，甚至造成系统不稳定。因此，稳态精度与动态性能、稳定性始终存在矛盾。在保证系统稳定的前提下，为实现提高稳态精度，可采用复合控制的措施来减小稳态误差。
1.按输入补偿的复合控制
设系统如图3-27所示，在输入端增加一补偿环节Gr（s），这时系统的闭环传递函数为
系统的稳态误差为 E（s）=R（s）-C（s）=R（s）[1-Φ（s）]
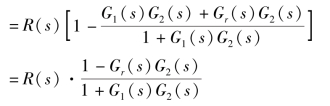
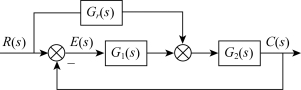
图3-27 输入补偿的复合控制系统
如果1-Gr（s）G2（s）=0，即
，E（s）=0。可见，增加输入补偿的复合控制，只要选取适当的补偿环节，可以减小甚至消除输入信号引起的稳态误差。同时，补偿环节Gr（s）位于闭环回路之外，结合闭环传递函数可以得到系统的特征方程没有改变，表明输入补偿复合控制不改变原系统的稳定性。
2.按扰动补偿的复合控制
设系统如图3-28所示，在扰动信号端增加一补偿环节Gd（s），引入到输入信号处，这时系统的闭环传递函数为
系统的稳态误差为
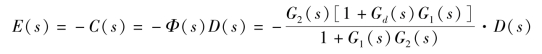
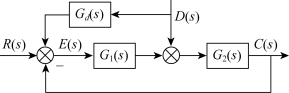
图3-28 扰动补偿的复合控制系统
如果1+Gd（s）G1（s）=0，即
，则E（s）=0。显然，增加扰动补偿的复合控制，只要选取适当的补偿环节，可以减小甚至消除扰动信号引起的稳态误差，且扰动补偿复合控制也不改变原系统的稳定性。
有关自动控制原理的文章
- 详细阅读
-
系统误差与稳态误差的解析与处理详细阅读
一般系统的误差是输出量的期望值与实际值之间的差值。由图3-24得出两个输入信号作用下的误差传递函数分别为则系统误差e可以看作是系统的误差响应。当时间t趋于无穷时，误差e的极限就是系统的稳态误差，即。由拉氏变换的终值定理可得式中，essr是参考输入信号作用下的稳态误差，essd是扰动信号作用下的稳态误差。根据上述讨论可知，系统的稳态误差不仅与系统的结构参数有关，还与输入信号的形式或作用点有关。......
2023-06-28
-
如何计算参考输入作用下的稳态误差？详细阅读
下面分别讨论典型输入信号作用下控制系统的稳态误差。表3-1给出了各种系统类型在不同输入信号作用下系统的稳态误差。但是在计算系统稳态误差前，必须先判断系统的稳定性；其次开环增益K必须是在开环传递函数标准形式下，与式相似；该规律只适用于参考输入信号作用下的计算，其他信号作用下应用终值定理计算。......
2023-06-28
-
消除方便船籍现象的措施详细阅读
授籍国对船舶进行有效管辖，也是授予船舶国籍不可忽视的因素，只有这样，才有可能避免方便船籍的一些弊端。国际法委员会的公海制度专题小组专门负责处理船舶国籍问题。这种意见为国际法委员会第三次会议所接受，并在国际法委员会第四次会议上通过一个确定船舶国籍取得条件最低要求的草案。......
2023-07-24
-
大学物理实验：消除系统误差的方法详细阅读
由于测量方法、测量对象、测量环境及测量人员不尽相同，因而没有一个普遍适用的方法来减小或消除系统误差。从产生系统误差的根源上消除。引入修正项消除系统误差。通过预先对仪器设备将要产生的系统误差进行分析计算，找出误差规律，从而找出修正公式或修正值，对测量结果进行修正。采用能消除系统误差的方法进行测量。......
2023-11-02
-
提高加工精度的有效措施详细阅读
保证和提高加工精度的方法，大致可概括为以下几种：减小原始误差法、补偿原始误差法、转移原始误差法、均分原始误差法、均化原始误差法、“就地加工”法。当原始误差是负值时人为误差就取正值，反之则取负值，并尽量使两者大小相等；或者利用一种原始误差去抵消另一种原始误差，也是尽量使两者大小相等、方向相反，从而达到减少加工误差、提高加工精度的目的。就地加工法在机械零件加工中常用来作为保证零件加工精度的有效措施。......
2023-06-29
-
系统误差产生原因及消除方法，一一解答详细阅读
产生的原因如下：①测量装置的因素：仪器设计原理的缺陷，仪器零件制造和安装不正确，仪器附件制造偏差等。消除系统误差的方法有：①选用公认的标准方法与所用方法作对比，从而找出校正数据。③尽量统一操作，如采用同一指示剂可以消除变色点和化学计量点不完全一致的误差；由同一个人操作可以消除各人掌握不一引起的种种误差等。......
2023-10-28
-
消除焊接残余应力的有效方法详细阅读
焊接残余应力存在于焊接结构中，会导致焊接结构的承载能力下降。事实证明，许多结构未进行消除焊接残余应力处理，也能安全运行。焊接残余应力形成的根源是近缝区在焊接过程中产生的压缩塑性变形。因此消除残余应力的实质就是使焊接区产生适量的塑性伸长。按其性质，消除焊接残余应力的方法可分为热处理法和机械法。（一）焊后热处理消除焊接残余应力焊后热处理也叫高温回火处理，是目前最常用的焊后热处理方法。......
2023-06-23
相关推荐