一般系统的误差是输出量的期望值与实际值之间的差值。由图3-24得出两个输入信号作用下的误差传递函数分别为则系统误差e可以看作是系统的误差响应。当时间t趋于无穷时,误差e的极限就是系统的稳态误差,即。由拉氏变换的终值定理可得式中,essr是参考输入信号作用下的稳态误差,essd是扰动信号作用下的稳态误差。根据上述讨论可知,系统的稳态误差不仅与系统的结构参数有关,还与输入信号的形式或作用点有关。......
2025-09-29
当扰动信号D(s)=0时,系统的稳态误差为
![]()
设系统的开环传递函数为
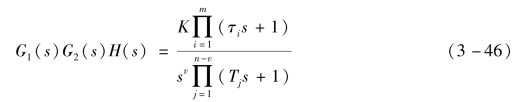
式中,K为系统的开环增益,τi、Tj为时间常数,v为积分环节的个数。系统类型通常是根据开环传递函数中积分环节的个数来分类的,当v=0,1,2时,则称系统为0型、Ⅰ型、Ⅱ型系统。
将式(3-46)代入式(3-45)可得
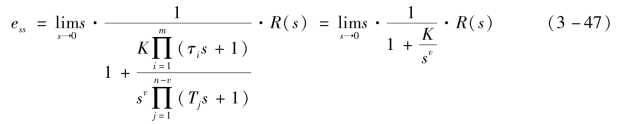
由式(3-47)可知,系统的稳态误差ess与开环增益K、积分环节个数v以及输入信号R(s)有关。下面分别讨论典型输入信号作用下控制系统的稳态误差。
1.阶跃信号作用下的系统稳态误差
设阶跃信号为r(t)=A·1(t),则![]() ,此时有
,此时有
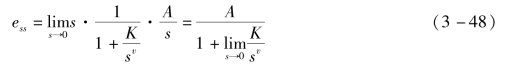
式中,A为阶跃信号的幅值。令![]() ,称Kp为静态位置误差系数。
,称Kp为静态位置误差系数。
由式(3-48)可得
当v=0时,Kp=K,则![]() ;
;
当v≥1时,Kp=∞,则ess=0。
可见,当系统在阶跃信号作用下,0型系统的稳态误差为定值,且ess与幅值A成正比,与开环增益K成反比,K越大,稳态误差越小,但误差始终存在,常称这类系统为有差系统;Ⅰ型及以上类型系统的稳态误差为零,此时为无差系统。
2.斜坡(速度)信号作用下的系统稳态误差
设斜坡信号为r(t)=At·1(t),则![]() ,此时有
,此时有
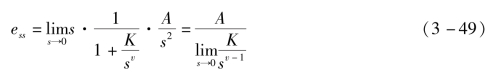
式中,A为斜坡信号的斜率。令![]() ,称Kp为静态速度误差系数。
,称Kp为静态速度误差系数。
由式(3-49)可得
当v=0时,Kv=0,则ess=∞;
当v=1时,Kv=K,则![]() ;
;
当v≥2时,Kv=∞,则ess=0。
可见,当系统在斜坡信号作用下,0型系统的稳态误差为无穷大,这时系统输出响应跟踪不上斜坡信号;Ⅰ型系统的稳态误差为定值,与斜率A成正比,与开环增益K成反比,K越大,稳态误差越小,表明输出能跟踪斜坡信号,但存在误差;Ⅱ型及以上类型系统的稳态误差为零,说明系统可以无误差跟踪斜坡信号。
3.抛物线(加速度)信号作用下的系统稳态误差(https://www.chuimin.cn)
设斜坡信号为![]() ,则
,则![]() ,此时有
,此时有
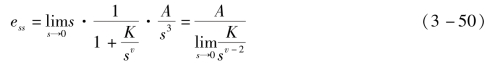
式中,A为抛物线信号的加速度。令![]() ,称Ka为静态加速度误差系数。
,称Ka为静态加速度误差系数。
由式(3-50)可得
当v≤1时,Ka=0,则ess=∞;
当v=2时,Ka=K,则![]() ;
;
当v≥3时,Ka=∞,则ess=0。
可见,当系统在抛物线信号作用下,0型和Ⅰ型系统的稳态误差为无穷大,这时系统输出响应不能跟踪输入信号;Ⅱ型系统的稳态误差为定值,与斜率A成正比,与开环增益K成反比,K越大,稳态误差越小,表明输出能跟踪输入信号;Ⅱ型以上类型系统的稳态误差为零,说明系统可以无误差跟踪输入信号。
表3-1给出了各种系统类型在不同输入信号作用下系统的稳态误差。
表3-1 输入信号作用下的稳态误差
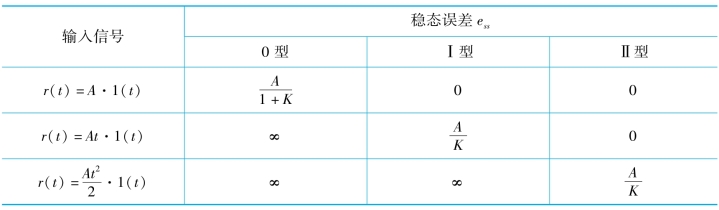
表3-1给出了稳态误差与系统结构、参数以及输入信号之间的规律,该规律可以直接得出系统的稳态误差,而不需要用终值定理计算。但是在计算系统稳态误差前,必须先判断系统的稳定性;其次开环增益K必须是在开环传递函数标准形式下,与式(3-46)相似;该规律只适用于参考输入信号作用下的计算,其他信号作用下应用终值定理计算。
例3-9 已知单位反馈控制系统的动态结构图如图3-25所示,试求:
(1)判断系统稳定性;
(2)当输入信号为r(t)=(1+2t+t2)·1(t),求系统的稳态误差。
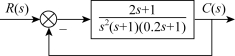
图3-25 系统结构图
解:(1)系统的稳定性
系统的闭环传递函数为
![]()
系统的特征方程为 s4+6s3+5s2+10s+5=0
列写劳斯表为
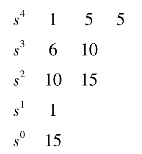
可见,劳斯表第一列系数均为正,则系统稳定。
(2)由图3-25可知,系统开环传递函数为![]() ,系统的类型为线性Ⅱ型系统,开环增益K=1。依据表3-1可得系统的稳态误差为ess=2。
,系统的类型为线性Ⅱ型系统,开环增益K=1。依据表3-1可得系统的稳态误差为ess=2。
相关文章

一般系统的误差是输出量的期望值与实际值之间的差值。由图3-24得出两个输入信号作用下的误差传递函数分别为则系统误差e可以看作是系统的误差响应。当时间t趋于无穷时,误差e的极限就是系统的稳态误差,即。由拉氏变换的终值定理可得式中,essr是参考输入信号作用下的稳态误差,essd是扰动信号作用下的稳态误差。根据上述讨论可知,系统的稳态误差不仅与系统的结构参数有关,还与输入信号的形式或作用点有关。......
2025-09-29

若k是按系统对稳态误差的要求选取的,则此项自然满足,可免去。需要校验的稳态误差可能包括:1.输入信号引起的误差e1)位置信号x=x0引起的误差eP。3)反馈传感器精度所引起的误差ε3不因k的改变而减少,故必须使反馈传感器有较高的精度。......
2025-09-29

对于Ⅰ、Ⅱ、Ⅲ类电能计量装置,应按整个装置的综合误差进行考核。表26图13.1.11 “查看分型结果”对话框图13.1.12 创建的型腔注对于安装1.0级有功电能表和0.5级互感器的Ⅰ类电能计量装置,其综合误差应符合Ⅱ类电能计量装置的综合误差的要求。电能计量装置的综合误差,在电能表的经常运行负载下,不应超过表26的规定。......
2025-09-29

只有当受激辐射的光子数多于受激吸收的光子数,介质才能对外表现出光的放大作用,才能成为激光工作介质。要实现粒子数的反转,首先介质本身的能级结构中应存在着亚稳态能级。亚稳态的存在有利于高能级上粒子的堆积,即利于实现高能级上粒子数大于低能级上的粒子数。能够产生粒子数反转分布的介质称为激活介质,也可称为激光器的工作介质。实现了粒子数反转后的激活介质对一定频率的光就具有放大作用,此时的激活介质称为增益介质。......
2025-09-29

对于临界条件则有10.1.2.2起动公式对粗颗粒泥沙,粘结力和附加静水压力远远小于重力,起动后仍在床面附近运动。在研究波浪作用下的泥沙起动问题时,通常只使用两种起动状态,即少量动和普遍动,国外以采用普遍动者居多。......
2025-09-29

稳态工况的喷油量由基本喷油量和修正喷油量组成。根据节气门开度和转速划分稳定工况的工况点,节气门开度范围为10%~100%,每隔10%取一个点,共10个点;转速范围1 000~8 000r/min,每隔1 000r/min取一个点,共8个工况点,共形成了80个工况点,分别对这80个工况点进行喷油量仿真计算,得到如图7.32所示的稳定工况喷油MAP图。图7.32稳定工况基本喷油量MAP图图7.32稳定工况基本喷油量MAP图......
2025-09-29
相关推荐