布洛芬是消炎止痛的西药，有一定的副作用，特别是对患有心脏疾病的人。布洛芬被混在天然产品中，既没有标识，也不知道含量，长期作为天然保健品服用，将产生不良后果。本方法用于检测天然产品中含有的布洛芬，为了提高灵敏度及确定性，采用了LC-UV-MS／MS的方法。另吸取990μL离心过的样品液，转入另一个2 mL注射瓶中，加入10μL布洛芬原始标准溶液，盖上盖子，摇匀，标上“添加样品液”。......
2023-07-02
劳斯判据的应用方法的分析介绍
【摘要】：除此之外，劳斯判据还有以下方面的应用。图3-20系统结构图解：系统的闭环传递函数为系统的特征方程为6s3+5s2+s+K=0。列出劳斯表为由劳斯判据可知，系统稳定的充要条件为，即K取值范围为。图3-22系统增加比例微分控制其闭环系统的传递函数变为特征方程为 2s3+s2+Kτs+K=0列出劳斯表为根据劳斯判据，系统稳定的条件为，可见只要选取适当的参数，系统便可稳定。
上述讨论可知，只要计算出系统特征方程，就可以依据劳斯判据来判别系统的稳定性。除此之外，劳斯判据还有以下方面的应用。
（1）按照系统的稳定性要求，利用劳斯判据来计算系统稳定时参数的取值范围。
例3-8 控制系统结构图如图3-20所示，试确定系统稳定放大倍数K的取值范围。
图3-20 系统结构图
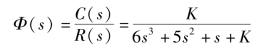
系统的特征方程为6s3+5s2+s+K=0。
列出劳斯表为
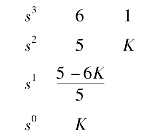
由劳斯判据可知，系统稳定的充要条件为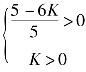
，即K取值范围为
。
（2）按照系统的稳定性要求，调整系统结构，并选择系统的参数，使系统稳定。
一个控制系统，如果无论怎样调整系统参数，系统始终不稳定，通常称这类系统为结构不稳定系统。
例3-9 结构不稳定系统结构图如图3-21所示，试设计方案使系统稳定。
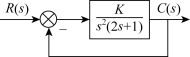
图3-21 结构不稳定系统
解：（方案一）闭环系统的传递函数为
特征方程为2s3+s2+K=0，依据劳斯判据可知，不论参数K取何值，系统总是不稳定。
为使系统稳定，可以通过增加辅助装置来解决。如在系统前向通道上加入比例微分控制，如图3-22所示。
图3-22 系统增加比例微分控制
其闭环系统的传递函数变为
特征方程为 2s3+s2+Kτs+K=0
列出劳斯表为
根据劳斯判据，系统稳定的条件为
，可见只要选取适当的参数，系统便可稳定。
（方案二）为使结构不稳定系统稳定，还可调整系统的结构，如积分环节外加单位负反馈，如图3-23所示。
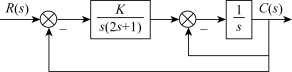
图3-23 调整系统结构
其闭环系统的传递函数变为
特征方程为 2s3+3s2+s+K=0
列出劳斯表为
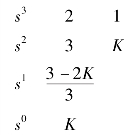
根据劳斯判据，系统稳定的条件为0＜K＜1.5，只要参数K选取适当，就可使系统稳定。
有关自动控制原理的文章
- 详细阅读
-
应用奈氏判据的例子详细阅读
例5-9 系统开环传递函数为应用奈氏稳定判据分析闭环系统稳定性。完整的开环幅相频率特性如图5-40所示。例5-12 设系统的开环传递函数为图5-42开环幅相频率特性试用对数频率稳定判据判断闭环系统的稳定性。图5-43系统伯德图由图5-43可见，在L（ω）＞0区段，相频特性曲线φ（ω）负穿越-180°线一次，根据奈氏稳定判据，N+≠N-，即闭环系统不稳定。......
2023-06-28
-
刃磨的方法及步骤的分析介绍详细阅读
简单刀具的种类很多，刃磨的部位主要是前、后刀面，其刃磨的方法和步骤基本相同，现简述如下。装夹圆柱铣刀、铲齿铣刀、面铣刀及三面刃铣刀时，均需用心轴紧固。图14-8 刃磨砂轮的修整a)碟形砂轮的修整b)碗形或杯形砂轮的修整4.刃磨平面刀具的刃磨 平面刀具有车刀、刨刀、刀片等，刃磨时可直接将刀具装夹在可倾虎钳上，不需加任何辅助装置即可调整所需位置刃磨各种角度。......
2023-06-28
-
添加几何关系的方法的分析介绍详细阅读
利用“添加几何关系”工具可以在草图实体之间或草图实体与基准面、基准轴、边线或顶点之间生成几何关系。使用“选择”按钮在草图上选择要添加几何关系的实体。此时,所选实体会在“添加几何关系”属性管理器中的“所选实体”列表框中显示,如图2-20所示。如果要删除已添加的几何关系,在“现有几何关系”列表框中右击该几何关系,再在弹出的快捷菜单中选择“删除”命令即可。......
2023-06-23
-
共同方法偏差检验的分析介绍详细阅读
共同方法偏差，也叫同源性偏差，指的是由于同样的数据来源或者评分人、同样的测量环境、题项语境与题项本身特征，所造成的自变量与因变量之间人为的共变，共同方法变异是一种系统误差。我们对本研究中变量的所有题项一起做因子分析，在本文中，问卷所有题项解释总变异为62.332%，第一个因子仅解释变异量的13.569%，这表明没有单一的一个因子解释了绝大部分的变异量，因此，可以看到本研究数据的同源误差问题并不严重。......
2023-08-02
-
姜氏测试方法的分析介绍，详细阅读
姜或姜的提取物一般测试6～10种标志性化合物就足够了，主要有姜辣素、姜烯酚、姜辣二醇和姜辣二酮。HPLC条件色谱柱：Phenomenex LUNA C18，5μm，4.6×250 mm，100 A移动相A：0.1%磷酸水溶液移动相B：0.1%磷酸乙腈溶液流速：1.0 mL／min柱温：室温UV 检测波长：282 nm注射量：20μL梯度：出峰次序：6-姜辣素、辣椒素、8-姜辣素、6-姜烯酚、6-姜辣二醇、6-姜辣二酮、10-姜辣素、8-姜烯酚、10-姜烯酚。......
2023-07-02
-
其他纺丝方法的介绍与应用详细阅读
Xu和Zhang利用凝胶纺丝和热拉伸制备了聚乙烯醇/单壁碳纳米管复合纳米纤维，实验结果显示复合纳米纤维与纯聚乙烯醇纳米纤维结构基本相同，但是拉伸强度由1.7 GPa增加至2.2 GPa，其纤维拉伸断裂面扫描电镜图如图1-11所示。表1-3拉伸倍数对聚丙烯腈纤维以及碳纳米管/聚丙烯腈复合纤维机械性能的影响......
2023-06-23
-
α-没药醇的测试方法的分析介绍详细阅读
α-没药醇，也称α-红没药醇，是春黄菊花中的一种有效成分，具有消炎作用。α-没药醇作为活性成分可保护和护理过敏性皮肤，故常用在护肤类化妆品中。此外，α-没药醇还可用于口腔卫生产品中，如牙膏和漱口水中。测试步骤①标准液的配制：准确称取10 mgα-没药醇标准品，转入50 mL容量瓶中，加入30 mL乙醇，超声至标准品全部溶解，再加入乙醇至刻度，摇匀后即可注射。......
2023-07-02
相关推荐