图3-10一阶系统的单位阶跃响应由图3-10可见，一阶系统的单位阶跃响应特点及系统的性能指标如下。响应曲线的初始斜率为1/T，表明一阶系统的单位阶跃响应若以初始速度等速上升至c（∞），所需要的时间恰好为时间常数T。图3-12一阶系统的单位斜坡响应由图3-11可以看出，经过一段时间，一阶系统的输出响应能同步跟随输入信号的变化，但是始终存在误差。......
2023-06-28
高阶系统的时域分析技巧
【摘要】：采用三阶及三阶以上微分方程描述的系统通常称为高阶系统。在控制工程中，几乎所有的控制系统均可视为高阶系统。由于高阶微分方程求解比较复杂，导致了高阶系统的时域分析和动态性能指标的计算比较困难。因此，只要熟悉一阶系统响应和二阶系统欠阻尼响应的特征，结合系统闭环零极点的特性，不难分析高阶系统。例3-3 已知系统的闭环传递函数为试用主导极点方法求系统动态性能指标tr、tp，ts和σ%。图3-18高阶系统的阶跃响应及性能指标
采用三阶及三阶以上微分方程描述的系统通常称为高阶系统。在控制工程中，几乎所有的控制系统均可视为高阶系统。由于高阶微分方程求解比较复杂，导致了高阶系统的时域分析和动态性能指标的计算比较困难。为了便于系统的分析和设计，通常抓住主要矛盾而忽略次要因素，利用闭环主导极点的概念，把高阶系统近似为一、二阶系统，进而估算高阶系统的性能指标。
设高阶系统闭环传递函数一般表达式为
假设系统的实极点为sj=-pj，共轭复极点为sl，l+1=-ζjωnk+jωdk，系统的零点为si=-zi。将式（3-37）写成传递函数零极点形式，即
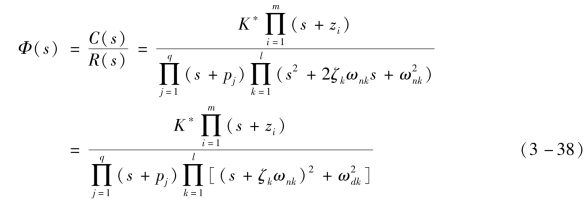
式中，q+2l=n，设pj、ζk、ωnk、ωdk均大于零。
设系统的输入信号为单位阶跃信号，系统的输出响应为
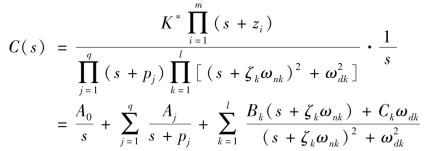
对上式进行拉氏反变换可得
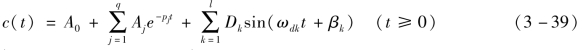
式中，
Bk和Ck为C（s）在对应极点处的留数。
由上述分析可以得出以下几点。
（1）系统单位阶跃响应分为稳态分量和瞬态分量两部分，由一阶系统和二阶系统的响应叠加而成。其中，稳态分量与输入信号相关，瞬态分量形式由系统闭环传递函数的极点性质决定。
（2）系统闭环传递函数极点离虚轴越远，则表明响应的瞬态分量衰减速度越快；反之离虚轴越近，其对应的瞬态分量衰减越慢，且该分量在瞬态过程中占的比重越大。如果一个极点或一对共轭极点离虚轴最近极点，周围没有其他零极点，其实部的绝对值比其他极点实部的绝对值小5倍以上，则称该极点为系统的主导极点。
（3）如果闭环系统中一个零点和一个极点相距很近，常称为一对偶极子。偶极子在瞬态响应中影响很小，可以忽略不计。在控制工程中，一般认为一对偶极子的距离比离虚轴的距离小一个数量级，可以认为这对零极点是偶极子对。
总之，在分析和设计高阶系统时，如果找到一个实数主导极点或一对共轭复数主导极点，高阶系统就可以近似成一阶系统或二阶系统来分析。因此，只要熟悉一阶系统响应和二阶系统欠阻尼响应的特征，结合系统闭环零极点的特性，不难分析高阶系统。
例3-3 已知系统的闭环传递函数为
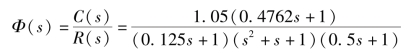
试用主导极点方法求系统动态性能指标tr、tp，ts和σ%。
解：闭环传递函数零极点表示形式为
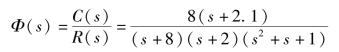
其中，零点z=-2.1，极点p1=-8、p2=-2、
显然，极点p3，4离虚轴最近且满足主导极点的条件，极点p2和零点z相距很近，是一对偶极子。因此，系统可近似为
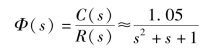
由二阶系统的性能指标计算公式可得
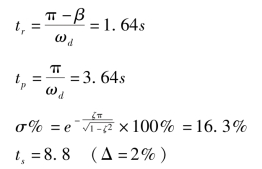
利用MATLAB软件，绘制出高阶系统的阶跃响应及性能指标如图3-18所示，可见经过处理简化后的系统与原系统的性能指标基本一致。
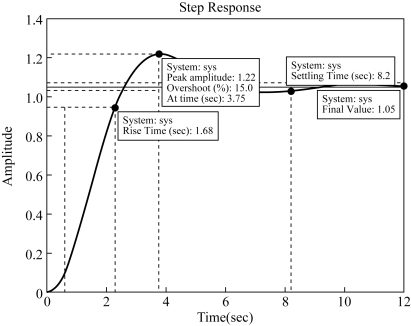
图3-18 高阶系统的阶跃响应及性能指标
有关自动控制原理的文章
- 详细阅读
-
新学习系统：培养高阶能力的教学变革详细阅读
它是综合运用分析性、创造性和实践性思维的能力，也是学习高阶知识、发展高阶思维和实现知识远迁移的能力。当前学生学习方式的变革是使学生由被动、惰性的学习转变为有意义的学习，培养学生的创新能力、问题求解能力、批判性思维等高阶能力。它发生在较高认知水平层次上或是运用较高层次认知能力的心智活动，需要学生充分运用创新、批判性思维以及问题求解和决策等系列高阶能力，积极主动进行意义建构。......
2023-08-08
-
MATLAB控制系统根轨迹分析应用技巧详细阅读
本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出线性控制系统根轨迹分析中常用的MATLAB命令。图4-19例4-9传递函数的零极点图例4-10 若单位负反馈控制系统的开环传递函数为绘制系统的根轨迹，并据根轨迹判定系统的稳定性。系统都是稳定的。图4-22例4-11传递函数的根轨迹图利用鼠标在根轨迹上选择K点：根轨迹图4-22，结合临界稳定值可知，系统稳定时，临界稳定时的阶跃响应曲线如图4-23所示。......
2023-06-28
-
低压油路系统使用与保养：技巧与故障案例分析详细阅读
②低压油路组成：单体泵燃油系统由燃油箱、低压输油泵、燃油滤清器、相应的油管等部件组成。而喷油器漏油的主要原因就是低压油路压力不足导致喷油器偶件穴蚀。所以应确保低压油路的压力并及时更换或清洁燃油滤清器。由于单体泵系统对燃油的预压要求较高，因此需要检测燃油系统的压力。......
2023-09-23
-
MATLAB在时域分析中的优势及应用案例介绍详细阅读
本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出时域分析时常用的MATLAB命令。例3-11 已知闭环系统传递函数为试用MATLAB判断系统的稳定性。图3-30例3-12系统的阶跃响应曲线图3-31例3-12系统的脉冲响应曲线例3-13 已知单位负反馈控制系统的开环传递函数为，试用MATLAB计算系统在单位阶跃信号作用下的tr、tp、ts、σ%。......
2023-06-28
-
PT泵燃油系统维修技巧-国Ⅲ柴油机故障分析详细阅读
PT泵燃油喷射系统的喷油器为主动式喷油，低压柴油在喷油器中通过摇臂压动喷油器的柱塞产生高压，喷油器也是一种柱塞泵，其驱动机构如图1-10所示。PT泵燃油喷射系统在动力性、经济性以及环保方面都优于直列泵喷油系统和分配泵喷油系统。PT泵燃油系统是康明斯K系列、N系列等机型专用的燃油喷射系统，已有电控PT泵燃油喷射系统。PT泵燃油系统中，燃油箱的位置高于PT泵和PT喷油器。......
2023-09-23
- 详细阅读
-
转向系统故障检修技巧详细阅读
有的人在转动转向盘的时候，往右转的力度大于往左转，如果长时间如此操作，转向助力系统ECU会根据这一习惯进行补偿，也就是电子助力系统经过自适应学习，才造成上述现象。为此，可以将向左转动转向盘的力度稍微加大些，争取将ECU的学习值纠正（补偿）过来。②转向液泵的传动带松弛。③转向盘转到了极限位置，转向助力系统内的压力达到最大。发生这种故障的原因是转向助力油路不畅通，油液循环受阻，需要更换转向助力泵和转向机。......
2023-08-30
相关推荐