二阶系统的性能评估指标

2023-06-28 理论教育版权反馈

【摘要】：由以上讨论可知，当二阶系统单位阶跃响应处于不同类型时，其响应结果具有较大差别，那么系统的性能指标计算也有所不同。由于欠阻尼情况下的二阶系统经常会遇到，在控制工程中也是经常希望的工作状态，因此下面将主要对欠阻尼二阶系统的性能指标进行计算和分析。

由以上讨论可知，当二阶系统单位阶跃响应处于不同类型时，其响应结果具有较大差别，那么系统的性能指标计算也有所不同。由于欠阻尼情况下的二阶系统经常会遇到，在控制工程中也是经常希望的工作状态，因此下面将主要对欠阻尼二阶系统的性能指标进行计算和分析。

1.上升时间tr

根据定义，上升时间tr是输出响应c（t）第一次达到稳态值所需要的时间，由式（3-23）可得

由于e-ζωntr≠0，故sin（ωdtr+β）=0，因此ωdtr+β=nπ （n=0，1，2，…）。根据上升时间定义，所以可得

式中， pagenumber_ebook=60,pagenumber_book=49

由式（3-26）可见，当阻尼比ζ一定时，上升时间tr与ωn成反比关系，系统初始响应速度与ωn成正比关系；当ωn一定时，tr与ζ成正比关系。

2.峰值时间tp

根据峰值时间tp的定义，将式（3-23）两边对时间t求导，并令其等于零，可得

整理得

于是得

式（3-27）表明，峰值时间tp与阻尼振荡频率成反比。当ωn一定，阻尼比ζ越小，tp越小，初始响应速度越快。

3.超调量σ%

将代入到式（3-23）中，可得

根据定义，且c（∞）=1，求得

式（3-28）表明，超调量只与阻尼比ζ有关，与自然振荡频率ωn无关。当阻尼比ζ越大，超调量σ%越小，平稳性越好。一般，在控制工程中，综合考虑系统的平稳性和快速性，常将ζ=0.707作为最佳阻尼比。

4.调节时间ts

根据定义，调节时间ts相对于稳态值c（∞）的波动小于某个给定值的最短时间，即

式中，Δ为5%或2%。

将式（3-23）代入式（3-28）中，可得

由于上述不等式求调节时间ts相当困难，因此常利用包络线来近似求取ts，当ζ＜0.8时，可近似得

由式（3-30）可见，调节时间ts与系统闭环极点实部成反比，闭环极点离虚轴越远，ts越小，系统响应速度越快

5.稳态误差ess

根据稳态误差的定义和拉普拉斯变换终值定理，当输入信号时，可得

当输入信号时，可得

式（3-31）表明，二阶系统在单位阶跃信号作用下，稳态误差为零。式（3-32）表明，如果输入信号为单位斜坡信号，则稳态误差正比于阻尼比ζ，与自然振荡频率ωn成反比。

例3-2 已知单位负反馈系统的开环传递函数为，设系统在单位阶跃信号作用下，计算动态性能指标tr，tp，σ%，ts。

解：系统的闭环传递函数为

根据标准二阶系统的闭环传递函数可得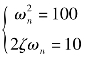 pagenumber_ebook=62,pagenumber_book=51

计算可得ζ=0.5，ωn=10rad/s，，β=1.047rad/s。

其动态性能指标为

上述讨论只是给出了欠阻尼情况下的二阶系统性能指标的求取，对于过阻尼二阶系统，由于单位阶跃响应无振荡、无超调，因此其动态性能指标只考虑调节时间ts。假设过阻尼二阶系统的特征根，则二阶系统可以近似为一阶系统，即

式中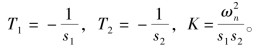， pagenumber_ebook=62,pagenumber_book=51

故过阻尼二阶系统的调节时间ts可近似为3T1（±5%误差带）或4T1（±2%误差带）。