求图1.18 电路中的理想电流源、图1.18 中的理想电压源发出的功率，再分别求出两等效电路中负载R上吸收的功率。......
2025-09-29
结构图的等效变换和简化法
【摘要】：为了便于分析和计算，需要将结构图中的一些方框基于“等效”的概念进行重新排列和整理，使复杂的结构图得以简化。图2-13n个方框串联的等效变换2.环节的并联传递函数分别为G1与G2的并联连接，如图2-14所示。其等效传递函数等于该两个传递函数的代数和。表2-1结构图简化的基本规则续表下面举例说明结构图的等效变换和简化过程。图2-17例2-7系统的结构图的化简例2-8 设系统的结构图如图2-18所示，试对其进行简化，并求闭环传递函数。
一个复杂的系统结构图，其方框间的连接必然是错综复杂的。为了便于分析和计算，需要将结构图中的一些方框基于“等效”的概念进行重新排列和整理，使复杂的结构图得以简化。由于方框间的基本连接方式只有串联、并联和反馈连接三种。因此，结构图简化的一般方法是移动引出点或比较点，将串联、并联和反馈连接的方框合并。在简化过程中应遵循变换前后变量关系保持不变的原则。
1.环节的串联
两个环节G1（s）和G2（s）以串联方式连接如图2-12（a）所示。两个传递函数分别为G1（s）与G2（s），以串联方式连接，如图2-12（a）所示。现欲将二者合并，用一个传递函数G（s）代替，并保持R（s）与C（s）的关系不变，即
图2-12 结构图串联连接及其简化
证明：由图2-12（a）图可写出：U（s）=G1（s）R（s）
消去U（s），则有C（s）=G1（s）G2（s）R（s）=G（s）R（s）
故可以证明等效结构如图2-12（b）所示。式（2-40）表明，两个传递函数串联的等效传递函数等于该两个传递函数的乘积。上述结论可以推广到多个方框图的串联。n个传递函数串联的等效传递函数，等于n个传递函数的乘积，如图2-13所示。
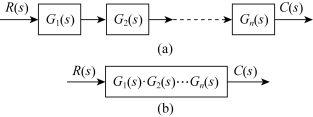
图2-13 n个方框串联的等效变换
2.环节的并联
传递函数分别为G1（s）与G2（s）的并联连接，如图2-14所示。其等效传递函数等于该两个传递函数的代数和。即
图2-14 两个方框并联的等效变换
证明：由图2-14（a）可写出：
可以证明等效结构图如图2-14（b）所示。
式（2-41）说明，两个传递函数并联的等效传递函数等于各传递函数的代数和。同样，可将上述结论推广到n个方框图的并联。
3.反馈连接的等效变换
如图2-15（a）所示为反馈连接的一般形式，其等效变换的结构图如图2-15（b）所示。
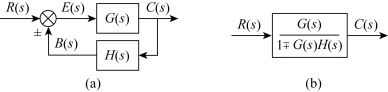
图2-15 反馈连接的等效变换
证明：由图2-15（a），按照信号传递的关系可写出：
C(s)=G(s)E(s)
B(s)=H(s)C(s)
E(s)=R(s)±B(S)(https://www.chuimin.cn)
消去E（s）、B（s），得
C(s)=G(s)[R(s)±H(s)C(s)]
[1∓G(s)H(s)]C(s)=G(s)R(s)
得
将反馈方框图等效简化为一个方框，方框中的传递函数应为上式。其闭环传递函数为
式中，分母中的减号对应于负反馈，加号对应于正反馈。
4.比较点和引出点的移动
在系统结构图简化过程中，有时为了便于进行方框的串联、并联或反馈连接的运算，需要移动比较点或引出点的位置。这时应注意在移动前后必须保持信号的等效性，而且比较点和引出点之间一般不宜交换位置。
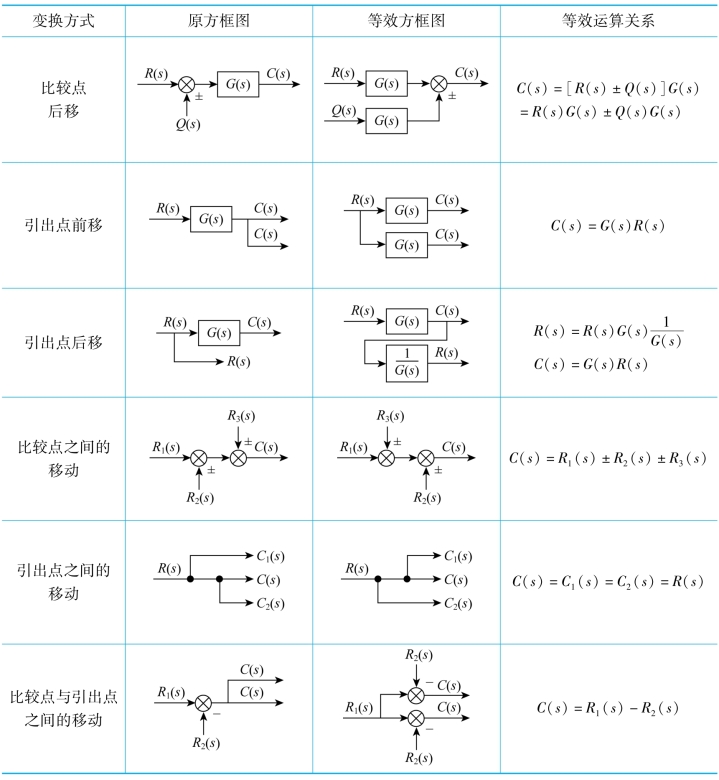
表2-1列出了结构图简化（等效变换）的基本规则。利用这些规则可以将比较复杂的系统结构图进行简化。
表2-1 结构图简化（等效变换）的基本规则
续表
下面举例说明结构图的等效变换和简化过程。
例2-7 试求如图2-16所示函数记录仪的闭环传递函数。
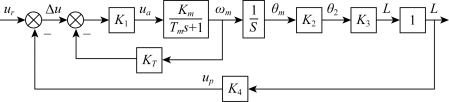
图2-16 例2-7系统的结构图
解：根据环节串联、并联和反馈连接的规则简化，其化简步骤如图2-17所示。
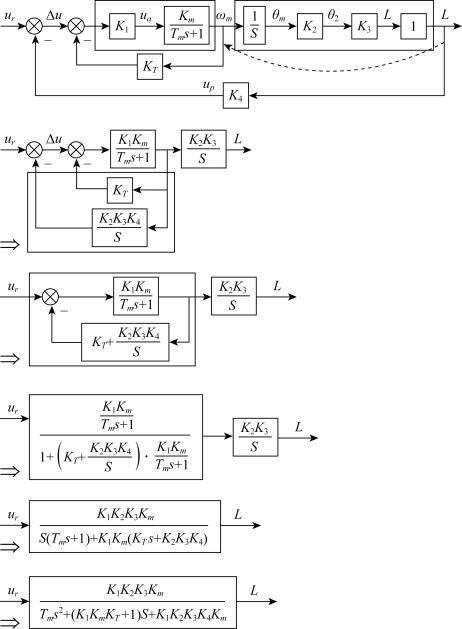
图2-17 例2-7系统的结构图的化简
例2-8 设系统的结构图如图2-18所示，试对其进行简化，并求闭环传递函数。
解：其步骤如图2-19所示。
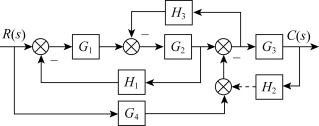
图2-18 例2-8系统的结构图
图2-19 例2-8系统的结构图的变换
相关文章
- 详细阅读
-
反激变换电路原理和优化设计详细阅读
S 关断后的电压为反激电路可以工作在电流断续和电流连续两种模式：图4.13反激电路原理图图4.14反激电路的工作波形①当S 开通时，W2 绕组中的电流尚未下降到零，则称电路工作于电流连续模式。反激变换电路结构简单，元器件数量少，因此成本低，广泛应用于较小功率的开关电源中。在各种家电、计算机设备、工业设备中广泛使用的小功率开关电源中，基本都采用的是反激变换电路。......
2025-09-29
-
坐标变换与变换矩阵详细阅读
坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2025-09-29
-
测量7.2.5A-D和D-A变换电路的方法详细阅读
图7-16 A-D转换器AD9883的内部功能框图2.VCD/DVD机中音频D-A变换电路的测量图解演示VCD/DVD机中音频D-A变换电路的测量如图7-17所示。图解演示D-A变换电路PCM1606供电电压的测量如图7-18所示。图7-18 D-A变换电路PCM1606供电电压的测量操作正常情况下，实测集成电路的供电电压约为5V。......
2025-09-29
-
三相和二相静止坐标系的变换：3s/2s变换详细阅读
一般将二相坐标系的α轴放在三相坐标系的A轴上，如图4.2所示，将三相磁动势FA、FB、FC投影到二相坐标系的α和β轴上，可以建立二相绕组与三相绕组的磁动势等效关系即以矩阵形式表示为并且二相/三相的变换关系为式中可以证明，C3s/2s、C2s/3s既是电流的变换矩阵，也是电压和磁链的变换矩阵。从式还可以看到，在二相静止坐标系上，二相电流iα、iβ的相位差为。......
2025-09-29
-
卡洛变换详解详细阅读
离散卡-洛变换是根据信号的统计特性性质进行正交展开。由式表示的变换称为离散卡-洛变换，系数向量g是信号向量通过该正交变换得到的，称之为主成分信号向量。离散卡-洛变换主要用于遥感多光谱信号中特征选择及数据压缩方面。因为是λi单调递减的，如果所选M个特征向量与M个最大特征值对应，那么用式来重建信号向量的误差最小，所以在最小均方误差的意义上讲，离散卡-洛变换是最优的。......
2025-09-29
-
二维沃尔什和哈达玛变换详解详细阅读
沃尔什基矩阵与一维变换时相同，由沃尔什函数产生。由沃尔什矩阵可以构成二维沃尔什函数的基本图像。表5-24 阶沃尔什基本图像矩阵与傅里叶基本图像不同的是，沃尔什变换等其他正交变换基图像均是实矩阵。二维哈达玛变换基矩阵与沃尔什基矩阵只是行向量排列顺序不同，正反变换形式相同。......
2025-09-29
-
LLC谐振变换拓扑的结构优化详细阅读
LLC谐振电路拓扑结构能够输出较大的功率，还须保证半桥处于零电压开关，具有高效率。如果FBP脚的电压低于0.51V，PFC电路被禁止，LLC级关闭。半桥LLC谐振控制器的FBL脚是反馈电压输入端，如果反馈电流大，则开关工作频率高。图4-22 PLC81OPG模块结构框图及引脚排列图......
2025-09-29
相关推荐