如图12.42所示，三个异地的数据中心之间需要定期或不定期地进行数据备份，数据的加密由量子加密机采用量子密钥和“一次一密”的加密方式完成，所需量子密钥由QKD 设备按需提供。在这种应用场景中，量子密钥的“信息理论安全”特点可极大地提高数据传输的安全性，满足企业和用户的高安全需求。图12.42基于QKD 的数据中心安全数据备份应用场景作为一种新的密钥分发功能组件，QKD 可以与现有ICT 技术结合应用。......
2023-06-26
传递函数示例——典型环节
【摘要】：比例环节的表达式为比例环节的传递函数为在物理系统中无弹性变形的杠杆、非线性和时间常数可以忽略不计的电子放大器、传动链之速比以及测速发电机的电压和转速的关系，都可以认为是比例环节。图2-7微分环节如图2-7所示的电路的微分方程为消去中间变量得相应的传递函数为式中，Tc=RC。称具有这种传递函数形式的环节为比例微分环节。一阶惯性环节的微分方程为其传递函数可以写成如下表达式：式中，K——比例系数；T——时间常数。
一个物理系统是由许多元件组合而成的。虽然各种元件的具体结构和作用原理是多种多样的，但若抛开其具体结构和物理特点，研究其运动规律和数学模型的共性，就可以划分成为数不多的几种典型环节。这些典型环节是：比例环节、微分环节、积分环节、比例微分环节、一阶惯性环节、二阶振荡环节和延迟环节。应该指出，由于典型环节是按数学模型的共性划分的，它和具体元件不一定是一一对应的。换句话说，典型环节只代表一种特定的运动规律，不一定是一种具体的元件。
1.比例环节
比例环节又称放大环节，其输出量与输入量之间的关系为一种固定的比例关系。这就是说，它的输出量能够无失真、无滞后地按一定的比例复现输入量。比例环节的表达式为
比例环节的传递函数为
在物理系统中无弹性变形的杠杆、非线性和时间常数可以忽略不计的电子放大器、传动链之速比以及测速发电机的电压和转速的关系，都可以认为是比例环节。但是也应指出，完全理想的比例环节在实际上是不存在的。杠杆和传动链中总存在弹性变形，输入信号的频率改变时电子放大器的放大系数也会发生变化，测速发电机电压与转速之间的关系也不完全是线性关系。因此，把上述这些环节当作比例环节是一种理想化的方法。在很多情况下，这样做既不影响问题的性质，又能使分析过程简化。但一定要注意理想化的条件和适用范围，以免导致错误的结论。
2.微分环节
微分环节是自动控制系统中经常应用的环节。
（1）理想微分环节。
理想微分环节的特点是在暂态过程中，输出量为输入量的微分，即
式中，τ——时间常数。
其传递函数为
如图2-7（c）所示的测速发电机，当其输入量为转角φ，输出量为电枢电压uc时，具有微分环节的作用。设测速发电机角速度为ω，则
，而测速发电机的输出电压uc与其角速度成正比，因此得
由此，传递函数为
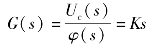
（2）实际微分环节。
这种理想的微分环节在实际中很难实现。如图2-7（a）所示的RC串联电路是实际中常用的微分环节的例子。
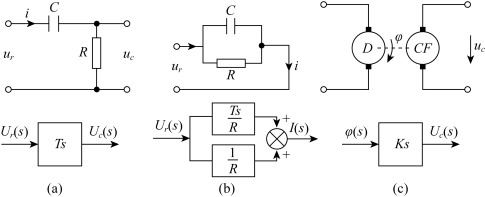
图2-7 微分环节
如图2-7（a）所示的电路的微分方程为
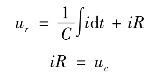
消去中间变量得
相应的传递函数为
式中，Tc=RC。
当RC≪1时，则其传递函数可以写成
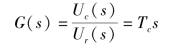
（3）比例微分环节。
如图2-7（b）所示的RC电路也是微分环节。它与如图2-7（a）所示的微分电路稍有不同，其输入量为电压ur，输出量为回路电流i。由电路原理知，当输入电压ur发生变化时，有
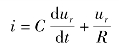
因此，该电路的传递函数为
式中，T=RC——微分时间常数。称具有这种传递函数形式的环节为比例微分环节。
3.积分环节
积分环节的动态方程为
上式表明，积分环节的输出量与输入量的积分成正比。
对应的传递函数为
4.一阶惯性环节
自动控制系统中经常包含有这种环节，这种环节具有一个储能元件。一阶惯性环节的微分方程为
其传递函数可以写成如下表达式：
式中，K——比例系数；T——时间常数。
如图2-8所示的RC电路就是一阶惯性环节的例子。
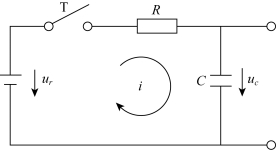
图2-8 RC电路
对于如图2-8所示的RC电路，其输入电压ur（t）和输出电压uc（t）之间的关系为
对上式进行拉氏变换，可以求出传递函数为
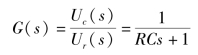
5.二阶振荡环节
二阶振荡环节的微分方程为
其传递函数为
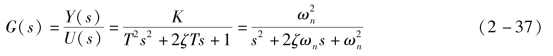
式中，T——时间常数，ζ——阻尼系数（阻尼比），ωn——无阻尼自然振荡频率。对于振荡环节恒有0≤ζ＜1。
6.延迟环节
延迟环节的特点是，其输出信号比输入信号滞后一定的时间。其数学表达式为
由拉氏变换的平移定理，可求得输出量在零初始条件下的拉氏变换为
Y(s)=U(s)e-τs
所以，延迟环节的传递函数为
在生产实际中，特别是在一些液压、气动或机械传动系统中，都可能遇到时间滞后现象。在计算机控制系统中，由于运算需要时间，也会出现时间延迟。
有关自动控制原理的文章
- 详细阅读
-
典型应用场景示例解析详细阅读
下面以潮汐效应业务模式下的基站聚合、多点协作传输两个应用场景示例，进一步说明光波与无线协同融合所带来的优势。图12.8展示了一个在潮汐效应业务模式下基站聚合方案示意图。如图12.9所示，对于移动用户1，协作的基站通过波长λ1连接到BBU1，将这种Co MP流量称为Intra-BBU 的Co MP。通过将小区的波长从λ2重构到λ1，组成了与BBU1相连的服务于U1和U2的Co MP小区，实现网络资源的高效利用。图12.10最大化Intra-BBU Co MP流量的波长重构技术......
2023-06-26
-
典型应用场景示例详细阅读
下面以机器学习在通信网络和数据中心网络中的两个应用场景示例，进一步说明通信与人工智能协同融合所带来的优势。图12.27信息通信网络中的机器学习机器学习在数据中心网络中的应用示例在数据中心网络中，针对多样化的业务请求，流量信息的预测与高效利用是网络资源智能、高效管理的核心需求。......
2023-06-26
-
典型环节频率特性分析详细阅读
图5-7理想微分环节的幅相频率特性②理想微分环节的伯德图。图5-11积分环节的奈氏图积分环节的对数幅相频率特性。惯性环节的频率特性为对数幅频特性是上述特性可用两条渐近线来近似。二阶微分环节的频率特性为对数幅频特性为对数相频特性为其对数频率特性如图5-18所示。......
2023-06-28
-
优化后：典型应用场景示例展示详细阅读
物联网是典型的应用和商业需求驱动的市场，本节讨论的NB-Io T、e MTC、LoRA 和Sigfox等技术都属于LPWA 范畴，解决5G 定义的大连接物联网需求。表12.2LPWA技术方案对比当前最成熟的应用是水表与电表的自动抄表应用，其他应用如路灯、停车场、自动贩卖机和物品跟踪等也在迅速增加。物联网是由多学科高度交叉形成的新兴前沿研究热点领域，目前在国际上备受关注。......
2023-06-26
-
典型应用场景示例优化详细阅读
下面以视频优化加速、车联网、增强现实三个应用场景示例，进一步说明通信与计算协同融合所带来的优势。图12.15车联网部署示意图随着连入车联网的车辆数量的增加，所需传输数据量增加，对时延的要求也更高。这使得附近的车辆能够在毫秒之内接收数据，从而允许驾驶员立即做出反应。图12.16增强现实应用示意图云计算、边缘计算、移动边缘计算等技术的出现，为信息通信网络面临的问题带来了新的解决方案。......
2023-06-26
-
MFC视频教程：消息传递函数使用和示例详细阅读
1）SendMessage和PostMessage函数都是消息传递函数，通过MSDN查看两个函数的格式。2个函数的4个参数的意义是一样的，只有返回值类型不同，LRESULT表示消息被处理后的返回值，BOOL表示消息是否传递成功。3）新建一个Win32工程，编写一段简单的代码测试消息传递函数。在MFC程序中，必须使用ON_MESSAGE来关联消息映射函数。PostMessage是非阻塞的，不等OnPostMessage执行完就继续向下执行，而且返回值是1，代表消息已经传送到。......
2023-11-25
-
实践环节不足：探究学好专业技术的五大环节详细阅读
实践环节少，是造成难题的主要原因。笔者认为，学好一门专业技术需要五大环节：理论学习环节、实验环节、实习环节、设计环节及产品制作环节。理论与实践相结合，学得会、学得活，记得牢、用得上，才能培养读者的创新意识。......
2023-06-28
相关推荐