首页理论教育传递函数的定义和性质详解

传递函数的定义和性质详解

2023-06-28 理论教育版权反馈

【摘要】：定义1 线性定常系统的传递函数，定义为零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。传递函数是复变量s的有理真分式函数，具有复变函数的所有性质。传递函数是系统或元件数学模型的另一种形式，是一种用系统参数表示输出量与输入量之间关系的表达式。传递函数与微分方程有相通性。下面举例说明求取简单环节的传递函数的步骤。

定义1 线性定常系统的传递函数，定义为零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。

设线性定常系统由下述n阶线性常微分方程来描述：

pagenumber_ebook=29,pagenumber_book=18

式中，y（t）是系统的输出量，u（t）是系统的输入量，ai（i=1，2，…，n）和bj（j=1，2，…，m）是与系统结构和参数有关的常系数。设u（t）和y（t）及各阶导数在t=0时的值均为零，即零初始条件，则对上式中各项分别求拉氏变换，并令Y（s）=ℓ[y（t）]，U（s）=ℓ[u（t）]，可得s的代数方程为

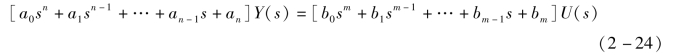
pagenumber_ebook=29,pagenumber_book=18

于是，由定义得系统传递函数为

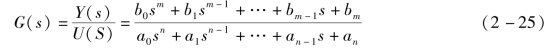
pagenumber_ebook=29,pagenumber_book=18

性质2 传递函数具有以下性质。

（1）传递函数是复变量s的有理真分式函数，具有复变函数的所有性质。m≤n且所有系数均为实数。

（2）传递函数是系统或元件数学模型的另一种形式，是一种用系统参数表示输出量与输入量之间关系的表达式。它只取决于系统或元件的结构和参数，而与输入量的形式无关，也不反映系统内部的任何信息。

（3）传递函数与微分方程有相通性。只要把系统或元件微分方程中各阶导数用相应阶次的变量s代替，就很容易求得系统或元件的传递函数。

（4）传递函数g（s）的拉氏反变换是脉冲响应g（t）。

g（t）是系统在单位脉冲δ（t）输入时的输出响应。此时U（s）=ℓ[δ（t）]=1，故有g（t）=ℓ-1[Y（s）]=ℓ-1[G（s）U（s）]=ℓ-1[G（s）]。

对于简单的系统或元件，首先列出它的输出量与输入量的微分方程，求其在零初始条件下的拉氏变换，然后由输出量与输入量的拉氏变换之比，即可求得系统的传递函数。对于较复杂的系统或元件，可以先将其分解成各局部环节，求得环节的传递函数，然后利用本章所介绍的结构图变换法则，计算系统总的传递函数。

下面举例说明求取简单环节的传递函数的步骤。

例2-6 图2-1中RLC网络的微分方程为

当初始条件为零时，拉氏变换为

(LCs2+RCs+1)Uc(s)=Ur(s)

则传递函数为

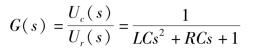
pagenumber_ebook=30,pagenumber_book=19