首页理论教育非线性数学模型线性化方法

非线性数学模型线性化方法

2025-09-29 理论教育版权反馈

【摘要】：在建立控制系统的数学模型时，常常会遇到非线性的问题。严格地说，实际物理元件或系统都是非线性的。这种线性化方法称为小偏差线性化方法。通过上述讨论，在非线性数学模型进行线性化时应注意以下几点。若非线性特性是不连续的，处处不能满足展开成为泰勒级数的条件，这时就不能进行线性化处理。这类非线性称为本质非线性，对于这类问题，要用非线性自动控制理论来解决。

在建立控制系统的数学模型时，常常会遇到非线性的问题。严格地说，实际物理元件或系统都是非线性的。例如，弹簧的刚度与其形变有关，因此弹簧系数K实际上是其位移x的函数，并非常值；电阻、电容、电感等参数与周围环境（温度、湿度、压力等）及流经它们的电流有关，也并非常值；电动机本身的摩擦、死区等非线性因素会使其运动方程复杂化而成为非线性方程。对于线性系统的数学模型的求解，可以借用工程数学中的拉氏变换，原则上总能获得较为准确的解答。而对于非线性微分方程则没有通用的解析求解方法，利用计算机可以对具体的非线性问题近似计算出结果，但难以求得各类非线性系统的普遍规律。因此，在理论研究时，考虑到工程实际特点，常常在合理的、可能的条件下将非线性方程近似处理为线性方程，即所谓线性化。

控制系统都有一个额定的工作状态以及与之相对应的工作点。由数学的级数理论可知，若函数在给定区域内有各阶导数存在，便可以在给定工作点的领域将非线性函数展开为泰勒级数。当偏差范围很小时，可以忽略级数展开式中偏差的高次项，从而得到只包含偏差一次项的线性化方程式。这种线性化方法称为小偏差线性化方法。

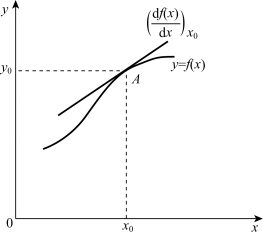
pagenumber_ebook=27,pagenumber_book=16

图2-5　小偏差线性化示意图

设连续变化的非线性函数为y=f（x），如图2-5所示。取某平衡状态A为工作点，对应有y0=f（x0）。当x=x0+Δx时，有y=y0+Δy。设函数y=f（x）在（x0，y0）点连续可微，则将它在该点附近用泰勒级数展开为

pagenumber_ebook=27,pagenumber_book=16

当增量（x-x0）很小时，略去其高次幂项，则有

令Δy=y-y0=f（x）-f（x0），Δx=x-x0，K=（df（x）/dx）x0，则线性化方程可简记为

Δy=KΔx

略去增量符号Δ，便得到函数在工作点附近的线性化方程为y=Kx。

式中，K=（df（x）/dx）x0是比例系数，它是函数y=f（x）在A点附近的切线斜率。

例2-5 铁芯线圈电路如图2-6（a）所示，其磁通Φ与线圈中电流i之间关系如图2-6（b）所示。试列写以ur为输入量，i为输出量的电路微分方程。

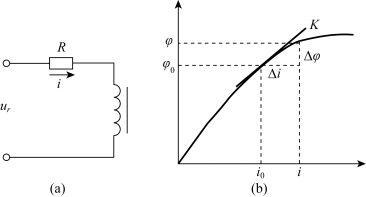
pagenumber_ebook=28,pagenumber_book=17

图2-6　铁芯线圈电路及其特性

解：设铁芯线圈磁通变化时产生的感应电势为

(https://www.chuimin.cn)

根据克希霍夫定律可写出电路微分方程为

式中，dΦ（i）/di是线圈中电流i的非线性函数，因此式（2-20）是一个非线性微分方程。

在工程应用中，如果电路的电压和电流只在某平衡点（u0，i0）附近作微小变化，则可设ur相对于u0的增量是Δur，i相对于i0的增量是Δi，并设Φ（i）在i0的附近连续可微，则将Φ（i）在i0附近用泰勒级数展开为

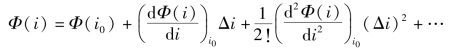
pagenumber_ebook=28,pagenumber_book=17

当Δi足够小时，略去高阶导数项，可得

式中，K=（dΦ（i）/di）i0，令ΔΦ=Φ（i）-Φ（i0），并略去增量符号Δ，便得到磁通Φ与线圈中电流i之间的增量线性化方程为

由式（2-21）可求得dΦ（i）/di=K，代入式（2-20）中，有

式（2-22）便是铁芯线圈电路在平衡点（u0，i0）的增量线性化方程，若平衡点发生变动，则K值亦相应改变。

通过上述讨论，在非线性数学模型进行线性化时应注意以下几点。

（1）线性化方程中的参数与选择的工作点有关，工作点不同，相应的参数也不同。因此，在进行线性化时，应首先确定工作点。

（2）当输入量变化范围较大时，用上述方法进行线性化处理势必引起较大的误差。所以，要注意它的条件，包括信号变化的范围。

（3）若非线性特性是不连续的，处处不能满足展开成为泰勒级数的条件，这时就不能进行线性化处理。这类非线性称为本质非线性，对于这类问题，要用非线性自动控制理论来解决。