1976年，Thompson教授首次在主动悬挂系统的研究中采用全状态反馈最优控制理论。随后，D.Hrovat和P.Barak通过某种途径探究了主动悬挂系统的优越性，结果显示安装了半主动和主动悬挂系统的车辆，其各项性能指标提高了很多。1990年，尼桑公司在Infinite Q45车型上装置了液压主动悬挂。此外，所设计的控制系统相对复杂、费用高昂，对主动悬挂系统控制策略的研究与结构设计有待进一步努力探究。......
2023-06-24
系统动态微分方程模型的选取
【摘要】：例2-1 列写如图2-1所示RLC网络的微分方程。列出原始微分方程式。将式（2-2）两边求导，得代入式（2-1）整理为显然，这是一个二阶线性微分方程，也就是如图2-1所示RLC无源网络的数学模型。因此，直流电动机的运动方程可以由以下三部分组成。现分别列写各元部件的微分方程。比较式（2-4）、（2-8）、和后发现，虽然它们所代表的系统的类别、结构完全不同，但表征其运动特征的微分方程式却是相似的。
常用的列写系统或环节的动态微分方程式的方法有两种：一种是机理分析法，即根据各环节所遵循的物理规律（如力学、电磁学、运动学、热学等）来列写；另一种方法是实验辨识法，即根据实验数据进行整理列写。在实际工作中，这两种方法是相辅相成的，由于机理分析法是基本的常用方法，本节着重讨论这种方法。
下面通过简单示例介绍机理分析法的一般步骤。
例2-1 列写如图2-1所示RLC网络的微分方程。
解：（1）明确输入、输出变量。
网络的输入量为电压ur（t），输出量为电压uc（t）。
（2）列出原始微分方程式。根据电路理论得
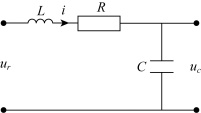
图2-1 RLC网络
而
式中，i（t）为网络电流，是除输入、输出量之外的中间变量。
（3）消去中间变量。
将式（2-2）两边求导，得
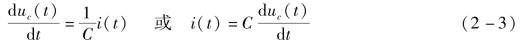
代入式（2-1）整理为
显然，这是一个二阶线性微分方程，也就是如图2-1所示RLC无源网络的数学模型。
例2-2 试列写如图2-2所示电枢控制直流电动机的微分方程，要求取电枢电压ua（t）（V）为输入量，电动机转速ωm（t）（rad/s）为输出量。图中Ra（Ω）、La（H）分别是电枢电路的电阻和电感，Mc（N·m）是折合到电动机轴上的总负载转矩。激磁磁通为常值。
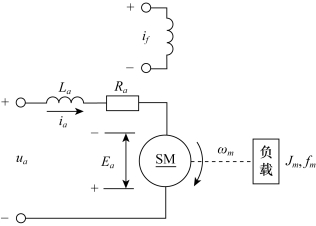
图2-2 电枢控制直流电动机原理图
解：电枢控制直流电动机是控制系统中常用的执行机构或控制对象，其工作实质是将输入的电能转换为机械能，也就是由输入的电枢电压ua（t）在电枢回路中产生电枢电流ia（t），再由电流ia（t）与激磁磁通相互作用产生电磁转矩Mm（t），从而拖动负载运动。因此，直流电动机的运动方程可以由以下三部分组成。
（1）电枢回路电压平衡方程：
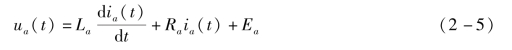
式中，Ea（V）是电枢反电势，它是当电枢旋转时产生的反电势，其大小与激磁磁通及转速成正比，方向与电枢电压ua（t）相反。
（2）电磁转矩方程。
式中，Cm（N·m/A）是电动机转矩系数，Mm（t）（N·m）是电枢电流产生的电磁转矩。（3）电动机轴上的转矩平衡方程。
式中，fm（N·m/rad/s）是电动机和负载折合到电动机轴上的黏性摩擦系数，Jm（kg·m·s2）是电动机和负载折合到电动机轴上的转动惯量。
由式（2-5）、式（2-6）和式（2-7）中消去中间变量ia（t）、Ea及Mm（t）便可得到以ωm（t）为输出量，以ua（t）为输入量的直流电动机微分方程为
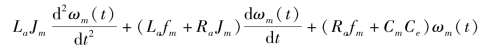
在工程应用中，由于电枢电路电感La较小，通常忽略不计，因而式（2-8）可简化为
式中，Tm=RaJm/（Rafm+CmCe）是电动机机电时间常数（单位为秒，s），K1=Cm/（Rafm+CmCe），K2=Ra/（Rafm+CmCe）是电动机传递系数。
如果电枢电阻Ra和电动机的转动惯量Jm都很小且忽略不计时，式（2-9）还可进一步简化为
这时，电动机的转速ωm（t）与电枢电压ua（t）成正比，于是电动机可作为测速发电机使用。
例2-3 如图2-3所示为一具有质量、弹簧、阻尼器的机械位移系统。试列写质量m在外力F（t）作用下，位移x（t）的运动方程。
解：设质量m相对于初始状态的位移、速度、加速度分别为x（t），dx（t）/dt，d2x（t）/dt2，由牛顿运动定律有
式中，F1（t）=f·dx（t）/dt是阻尼器的阻尼力，其方向与运动方向相反，其大小与运动速度成正比，f为阻尼系数；F2（t）=Kx（t）是弹簧弹性力，其方向亦与运动方向相反，其大小与位移成正比，K为弹性系数。将F1（t）和F2（t）代入式（2-11）中，经整理后即得该系统的微分方程式为
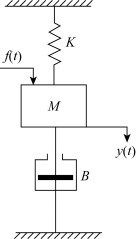
图2-3 弹簧—质量—阻尼器机械位移系统
例2-4 试列写如图2-4所示速度控制系统的微分方程。
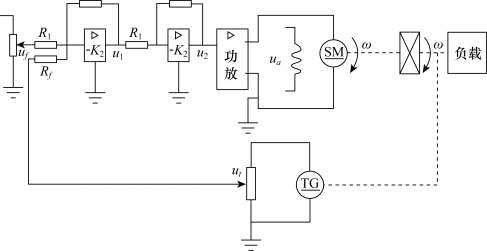
图2-4 速度控制系统
解：通过分析图2-4可知控制系统的被控对象是电动机（带负载），系统的输出量ω是转速，输入量是ug，控制系统由给定电位器、运算放大器Ⅰ（含比较作用）、运算放大器Ⅱ（含RC校正网络）、功率放大器、测速发电机、减速器等部分组成。现分别列写各元部件的微分方程。
（1）运算放大器Ⅰ。输入量（即给定电压）ug与速度反馈电压uf在此合成产生偏差电压并经放大，即
式中，K1=R2/R1是运算放大器Ⅰ的比例系数。
（2）运算放大器Ⅱ。考虑RC校正网络，u2与u1之间的微分方程为
式中，K2=R2/R1是运算放大器Ⅱ的比例系数，τ=RC是微分时间常数。
（3）功率放大器。本系统采用晶闸管整流装置，它包括触发电路和晶闸管主回路。忽略晶闸管控制电路的时间滞后，其输入输出方程为
式中，K3为比例系数。
（4）直流电动机。直接引用例2-2所求得的直流电动机的微分方程式（2-9）：
式中，Tm、Km、Kc及M′c均是考虑齿轮系和负载后，折算到电动机轴上的等效值。
（5）齿轮系。设齿轮系的速比为i，则电动机转速ωm经齿轮系减速后变为ω，故有
（6）测速发电机。测速发电机的输出电压uf与其转速ω成正比，即有
式中，Kt是测速发电机比例系数（V/rad/s）。
从上述各方程中消去中间变量，经整理后便得到控制系统的微分方程：
式中，T′m=（iTm+K1K2K3KmKtτ）/（i+K1K2K3KmKt）
K′g=K1K2K3Kmτ/(i+K1K2K3KmKt)Kg=K1K2K3Km/(i+K1K2K3KmKt)
K′c=Kc/(i+K1K2K3KmKt)
综上所述，列写控制系统微分方程式的步骤可归纳如下：
（1）根据元件的工作原理及其在控制系统中的作用，确定其输入量和输出量；
（2）分析元件工作中所遵循的物理规律或化学规律，列写相应的微分方程；
（3）消去中间变量，得到输出量与输入量之间关系的微分方程，即数学模型。
比较式（2-4）、（2-8）、（2-12）和（2-19）后发现，虽然它们所代表的系统的类别、结构完全不同，但表征其运动特征的微分方程式却是相似的。从这里也可以看出，尽管环节（或系统）的物理性质不同，它们的数学模型却可以是相似的。这就是系统的相似性，利用这个性质，就可以用那些数学模型容易建立，参数调节方便的系统作为模型，代替实际系统从事实验研究。
有关自动控制原理的文章
- 详细阅读
-
频率动态仿真误差模型的建立与优化详细阅读
基于上述定义的频率动态轨迹的特征指标，建立误差模型函数。依据所研究的频率动态问题，分别在每组确定的系统参数下，首先选取若干个有实际参考意义的频率实测轨迹；其次利用电力系统仿真软件仿真得到频率仿真轨迹；然后通过上述已建立的单功率脱落事件下的误差模型计算误差值，并对这些样本进行两两比较，形成判断矩阵；最后通过对判断矩阵进行求解，得到各个样本的权重系数。......
2023-06-29
-
柯氏评估模型修正发展的动态进展详细阅读
柯氏模型是最早用来指导研究培训效果的评估模型,其思想和方法对于后世的培训评估研究具有深远的指导意义。投资回报率是财会概念,体现的是组织的经济利益,是大多数社会组织追求的最终目的,在评估模型中引入投资回报率大大增加了评估模型的应用范围。......
2023-12-03
-
分析EPC系统的动态特性详细阅读
由系统的传递函数框图可得EPC系统的开环传递函数为式中 k——开环放大系数，。将算得的ωh、ξh、k代入式，可据此画出EPC系统的开环伯德图。图12-18 改造前后CP机组EPC系统的开环伯德图由图12-18可得系统的性能指标为：①穿越频率：ωc=2.4Hz；②幅值裕量：h=16dB；③相位裕度：γ=75°。可见实测值和理论分析值比较接近，说明上面建立的EPC系统的数学模型和确定的参数是正确的，是可以作为预测改造后系统性能的依据的。......
2023-06-15
-
风力发电系统中双馈发电机动态数学模型详细阅读
风力发电的实质是通过叶片捕获风能并将其转化为机械能，经过传动系统后通过发电机再将机械能转化为电能的过程。如果按发电机的转子转速是否与同步转速一致来区分异步发电机或同步发电机，则交流励磁双馈发电机应当被称为异步发电机。但是，从外特性来看，交流励磁发电机在很多地方又与同步发电机类似。因此，有些学者也把交流励磁发电机称为异步化同步发电机。......
2023-06-23
-
校验系统动态品质的重要性详细阅读
根据对系统的要求，对恒值系统需校验的指标可能是σ、ts、ω0.7，对随动系统需校验的指标可能是σ、tr、ω0.7。3）当L（ω）以-60dB/dec的斜率穿越横轴时，系统将不能满足稳态误差和动态品质的要求。......
2023-06-15
-
动态气门系统：提升引擎效率的新技术详细阅读
动态气门系统由凸轮、升降器或从动件、驱动凸轮旋转的凸轮轴、驱动凸轮轴旋转的正时链条或正时带等组成。动态气门系统在发动机的全部运行范围内传递负荷。在低速状态，气门系统的负荷仅为弹簧力，但在高速状态还包括构成气门系统的各部件质量的惯性力。图9-16 各种气门传动机构气门的摩擦力根据临界接触范围，即凸轮轴轴颈轴承、摇臂/支撑、凸轮/挺杆接触面的不同而不同。......
2023-06-28
-
电弧二维动态数学模型探究详细阅读
对SF6断路器近区故障开断能力进行数值分析，首先应建立开断过程动态数学模型，因为电弧、灭弧室、喷口和动静触头等具有轴对称形状，且以灭弧室中轴线为其对称轴，所建数学模型在空间上为二维轴对称。采用K-ε两方程模型来描述湍流效应。......
2023-07-02
相关推荐