，xn｝输出：未知样本X所属类别号3.朴素贝叶斯分类算法演示表3-9朴素贝叶斯示例数据集样本X7=｛打喷嚏，建筑工人，？朴素贝叶斯分类算法的优点在于容易实现，在大多数情况下所获得的结果比较好。......
2023-11-08
贝叶斯决策理论：处理模式分类问题的基本理论
【摘要】：贝叶斯决策理论是统计方法处理模式分类问题的基本理论之一。那么，利用贝叶斯公式可以得到后验概率基于最小错误率的贝叶斯决策规则为：如果，也就是说，如果p，那么将模式x赋予类ωi，即x∈ωi。上述理论中，每个类的出现概率以模式的条件概率密度函数必须是已知的。由于这些原因，贝叶斯决策理论在实际应用中通常要假设各种概率密度函数的解析式，以及从每类样本模式估计的必要参数。
贝叶斯决策理论（Bayesian Decision Theory）是统计方法处理模式分类问题的基本理论之一。假设研究的分类问题有N个类别，每个类别ωi（i=1，2，…，N）出现的先验概率为P (ωi)。在特征空间已经观察到某个特定的模式x，且条件概率密度函数p (x｜ωi)是已知的。那么，利用贝叶斯公式可以得到后验概率
基于最小错误率的贝叶斯决策规则为：如果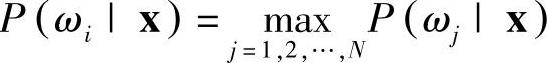
，也就是说，如果p
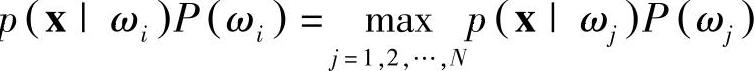，那么将模式x赋予类ωi，即x∈ωi。
上述理论中，每个类的出现概率以模式的条件概率密度函数必须是已知的。前者的获取通常并不构成问题，比如，当所有类的出现概率大致相同，则可令P(ωi)=1／N，即使这个条件不正确，我们也可以通过对问题的认识推算出这些先验概率。而后者的估计就是另一回事了，如果模式向量x是n维的，那么p (x｜ωi)就是一个n元函数，如果它的形式是未知的，就需要使用多元概率理论的方法对它进行估计。这类方法在实际应用中非常困难，尤其是代表每个类别的模式数目不大，或隐含的概率密度函数形式的规律性不强时更是如此。由于这些原因，贝叶斯决策理论在实际应用中通常要假设各种概率密度函数的解析式，以及从每类样本模式估计的必要参数。目前，对p (x｜ωi)的最为普遍的假设形式是高斯概率密度函数［8］。
有关图像目标的表示与识别的文章
- 详细阅读
-
基于朴素贝叶斯的分类器介绍详细阅读
朴素贝叶斯分类器进行目标分类的基本思想是利用特征项和类别的联合概率来估计给定目标的类别概率。理论上，朴素贝叶斯分类器与其他分类方法相比具有最小的误差率。但是该模型在分类识别中假设特征项之间相互独立，而这个假设在实际应用中往往是不成立的，这给朴素贝叶斯分类器的正确分类带来了一定影响。因此，近年来大量的研究工作致力于改进朴素贝叶斯分类器，主要集中在选择特征子集和放松独立性假设在两个方面。......
2023-06-28
-
模型结构：散户的贝叶斯决策组合和风险资产策略详细阅读
若散户们的决策组合为b单位的货币、α单位的风险资产，则散户的最优策略为如下最优化问题的解：其中，g（θ|v）为散户观察到证券均衡价格后关于取值θ的后验概率信念。博弈所用的均衡是完美贝叶斯均衡，它是指一对策略和一组后验信念g（.|.），满足：散户为贝叶斯理性，即对任给的可行v，g（.|v）是观测到证券均衡价格v后，基于先验信念，按贝叶斯推断形成的对取值θ的后验信念。......
2023-07-22
-
高等教育学：基本理论问题详细阅读
四逻辑实证主义者罗素的高等教育思想罗素是现代英国著名的逻辑实证主义哲学家，他的高等教育思想虽不及赫钦斯、雅斯贝尔斯等丰富，但他提出了一些具有启发意义的观点。罗素的高等教育思想产生于20世纪20年代。这是贯穿在19世纪以来高等教育发展过程中的一个重要问题。五新托马斯主义者马利坦的高等教育思想马利坦是现代新托马斯主义哲学流派的著名代表人物。他的高等教育思想是其整个教育思想的一个组成部分。......
2024-01-22
-
学与教的基本理论：解决问题的研究概述详细阅读
解决问题也就是机体获得对新的刺激情境做出适当反应的过程。格式塔心理学家为了便于与行为主义进行争论，用动物作为被试者研究解决问题。杜威提出的反省思维五个阶段被后人称为解决问题的五个阶段，并被广为引用。......
2024-01-21
-
基于贝叶斯网络的相关分析方法优化详细阅读
贝叶斯网络是基于概率分析和图论对不确定性知识进行表示的推理模型，它是一种模拟人类推理过程中因果关系的不确定性处理模型。贝叶斯分类器是用于分类的贝叶斯网络，它是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。通过对纽约市曼哈顿区2014年至2017年的交通事故数据构造朴素贝叶斯网络，对事故中伤亡人数进行分析。图4.1相关性分析结果......
2023-06-15
-
问题探究教学模式及理论基础详细阅读
我提出的“问题探究教学模式”建立在问题探究教学与发现学习理论基础上，这两种教学理论都强调学生自主参与构建自己的知识结构，都强调找到新旧学习内容之间的本质联系，强调归纳推理方法的应用。（二）概念问题探究教学模式是指根据教学内容及要求，由教师创设问题情境，以问题的发现、探究和解决来激发学生的求知欲、创造欲和主体意识，逐渐培养学生养成质疑的习惯，逐步提高学生的创造性思维和创新能力的一种教学模式。......
2023-08-04
-
条件概率、乘法公式、全概率公式、贝叶斯公式解详细阅读
，Bn两两互不相容，且满足B1∪B2∪…∪Bn=Ω），则当P>0（i=1，2，…，n）时，对任意事件A有注 使用全概率公式解题时，可按以下原则寻找完全事件组B1，B2，…，Bn都较A先发生.贝叶斯公式：设B1，B2，…精解 先引入有关事件：A1={甲表演}，A2={乙表演}，A3={丙表演}，B={一次命中一次未命中}，则由于B与A1，A2，A3有关，且A1，A2，A3是发生于B之前的一个完全事件组，因此由全概率公式得所以......
2023-10-27
相关推荐