【主要内容】设二元函数z=f（x，y）在点（x0，y0）的某个邻域内有定义.如果它在点（x0，y0）处的全增量Δz=f（x0+Δx，y0+Δy）-f（x0，y0）可以表示为Δz=AΔx+BΔy+o（ρ）（其中A和B不依赖于Δx，Δy，o（ρ）是比ρ=高阶的无穷小），则称z=f（x，y）在点（x0，y0）处可微，称AΔx+BΔy为z=f（x，y）在点（x0，y0）处的全微分，记为，即注 （ⅰ）二元函......
2023-10-27
符号串及其运算符号集合的定义与性质
【摘要】：典型的符号有字母、数字、各种标点符号和各种运算符。定义B-7（符号串）由符号集∑中0个或多个符号相连而成的有穷序列称为∑上的符号串。包括空串在内的∑上符号串的全体记为∑。如果x是符号串，把x自身连接n(n≥0)次得到的符号串x，称为x的n次方幂，记作xn。定义B-11设V是符号集∑上的一个符号串集合，则V的正闭包定义为V的闭包定义为例如：V={a，b}，则V+={a，b，aa，ab，ba，bb，aaa，aab，…
定义B-6（符号集）符号集∑是符号元素的非空有穷集合。典型的符号有字母、数字、各种标点符号和各种运算符。
例如，集合{a，b，c，+，∗}是一个含有5个符号的符号集，而符号集{0，1}只有两个符号。
定义B-7（符号串）由符号集∑中0个或多个符号相连而成的有穷序列称为∑上的符号串。特殊地，不包括任何符号的符号串称为空串，记作ε。包括空串在内的∑上符号串的全体记为∑∗。
例如，有符号集{a，b，c，+，∗}，则a，b，c，+，∗，aa，ab，a+，a∗，aaa，c+∗等等都是该符号集上的符号串。
定义B-8（符号串的长度）若x是符号集∑上的符号串，那么，其长度指x中所含符号的个数，记为x。
例如：abc=3，abc+∗abc=8，而ε=0。
“连接”和“闭包”是符号串操作中的两种基本运算。
定义B-9（符号串的连接）假定x，y是符号集∑上的符号串，则把y的各个符号依次写在x符号串之后得到的符号串称为x与y的连接，记作xy。
例如：∑={a，b，c}，x=abc，y=cba，那么，xy=abccba。
如果x是符号串，把x自身连接n(n≥0)次得到的符号串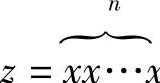
x，称为x的n次方幂，记作xn。当n=0时，x0=ε。当n≥1时，xn=xxn-1=xn-1x。
定义B-10（集合的乘积运算）设A，B是符号集∑上的两个符号串集合，则A和B的乘积定义为
其中，A0={ε}。当n≥1时，An=An-1A=AAn-1。
定义B-11（集合的闭包运算）设V是符号集∑上的一个符号串集合，则V的正闭包定义为
V的闭包定义为
例如：V={a，b}，则
V+={a，b，aa，ab，ba，bb，aaa，aab，…}
V∗={ε，a，b，aa，ab，ba，bb，aaa，aab，…}
有关图像目标的表示与识别的文章
- 详细阅读
-
高等代数中集合与其运算-高等代数详细阅读
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2023-11-22
-
子极限的定义与性质，自变量的变化过程及其限制详细阅读
上面我们讨论了x→x0与x→∞时函数极限的定义及性质，其中自变量的变化过程x→x0是指自变量x沿x轴从x0的左、右两侧趋于x0，x→∞是指自变量x沿x轴左、右两侧离原点越来越远，趋于无穷远.但有时所讨论的极限中，其自变量的变化过程只须沿某一侧（左侧或右侧）变化，例如考察极限时，由于受函数的定义域限制，自变量在x→0的变化过程中，x只能从0的右侧趋近于0，该变化过程相当于在变化过程“x→0”中增加了......
2023-11-19
-
高考数学有套路-专题集合概念与运算详细阅读
A.{2}B.{4，6}C.{1，3，5}D.{2，4，6}20.设全集U=R，集合A={x|x2-2x-3＜0}，B={x|x-1≥0}，则图中阴影部分所表示的集合为（）.A.{x|x≤-1或x≥3}B.{x|x＜1或x≥3}C.{x|x≤1}D.{x|x≤-1}21.已知A，B均为集合U={1，3，5，7，9}的子集，且A∩B={3}，UB∩A={9}，则A等于（）.A.{1，3}B.{3，7，9}C.{3，5，9}D.{3，9}......
2023-10-15
-
传统集合运算-数据库技术应用详细阅读
传统的集合运算是目运算，它包括并、差、交、广义笛卡儿积共4种运算。设关系R和S具有相同的目n，且相应的属性取自同一个域，则定义并、差、交运算如下。若R有k1个元组，S有k2个元组，则关系R和关系S的广义笛卡儿积应当有k1×k2个元组。R和S的笛卡儿积表示为......
2023-11-24
-
数学中的连续函数之定义与性质详细阅读
现实生活中，很多变量的变化是连续不断的，比如气温的变化、植物的生长、物体受热时面积的变化等，都是连续的变化.这种现象在数学上用函数的连续性来反映和研究.一、连续函数的概念定义1.21 在函数y=f（x）的定义域中，设自变量x由x0变到x1，差Δx=x1-x0叫做自变量x的增量（改变量），相应的函数值的差Δy=f（x1）-f（x0）=f（x0+Δx）-f（x0）叫做函数y=f（x）的增量（见图1-1......
2023-11-22
-
计算机导论-算法定义与性质详细阅读
在第1章我们简单介绍了算法的概念，并指出：软件的主体是程序，程序的核心是算法。算法既是人类之间交流智能的工具，也是人和机器之间交流智能的工具。算法的可终止性是指算法应能在有限的操作步骤后结束。我们仍以第1章给出的求解两个整数的最大公约数问题的算法为例，来讨论算法的定义问题。所以，上述方法不是一个算法。计算机求解任何问题，必须在一个有限的时间段内得到处理结果，算法的可终止性保证了这一点。......
2023-11-18
-
数学符号的创用及其影响详细阅读
例如,法国数学家克莱罗曾建议用大写希腊字母作为函数符号,如∏x,Φx,Δx 等。对于函数定义,欧拉先后给出了三个。后又把函数定义为“任意画出的一条曲线”。欧拉被后人称为“数学家之英雄”,是因为其顽强拼搏的毅力和惊人的创造力震撼了世人的心灵。图2.3.4数学看起来高深莫测可见,数学符号中不仅有英文字母,还有希腊字母,这是沿用了历史上数学家的做法,即约定俗成。......
2023-11-23
相关推荐