使用特征和BP网络进行目标分类的实验研究

2023-06-28 理论教育版权反馈

【摘要】：实验3：基于角点标记图与BP网络的目标分类近年来，傅里叶描绘子、标记图和不变矩特征被广泛应用于目标识别领域。图7-11 五种特征在视点变化下的识别效果实验4：增加训练模式后的分类效果改进通过下面的训练方法尝试进一步提高系统的识别能力：在使用基准视点的投影图进行训练之后，用余下的训练集数据对系统进行重新训练，再用新权值向量通过系统运行测试集样本来确立识别性能。

普林斯顿大学三维模型库（Princeton Shape Benchmark）^［209］经常被用来研究与3D模型相关算法的优劣。这个公用平台中提供了多达1800个三维模型作为待识别目标，如图7-9所示，可以对其进行不同视角的投影拍摄来建立一个符合自己实验要求的目标图库。

图7-9 普林斯顿大学三维模型库示例

本书从普林斯顿大学三维模型库中挑选出六个飞机模型、一个T60坦克模型、一个小汽车模型用来衡量目标识别系统的性能，其中六个飞机模型的型号依次是F16，F117，M1237，747G，F1，F2。图7-10就是采用7.2节提出的方法获得的基准视点下的3D模型2D投影图。

图7-10 3D模型的2D投影图表示

实验1：利用基准角点进行目标匹配

由于基准角点的提出是针对飞机图像的，本实验选用了六个飞机模型在不同视点下的投影图：在每个模型的单位球上，从北纬90°到北纬60°，纬度每隔5°、经度取固定值（与机身最长轴线垂直）进行一次投影，每个模型都得到7幅投影图，样本数量共计6×7=42。我们使用每个飞机模型在基准视点的投影图作为模板，并通过F16战斗机的所有样本对其进行相似性度量，表7-1是F-16战斗机投影图（不同视点下）与其他飞机投影图（基准视点下）的特征描述子S的比例。1表示样本与模板完全吻合，数值与1做差的绝对值越大则表示样本与模板越不匹配。

表7-1利用基准角点进行目标匹配的相似度结果

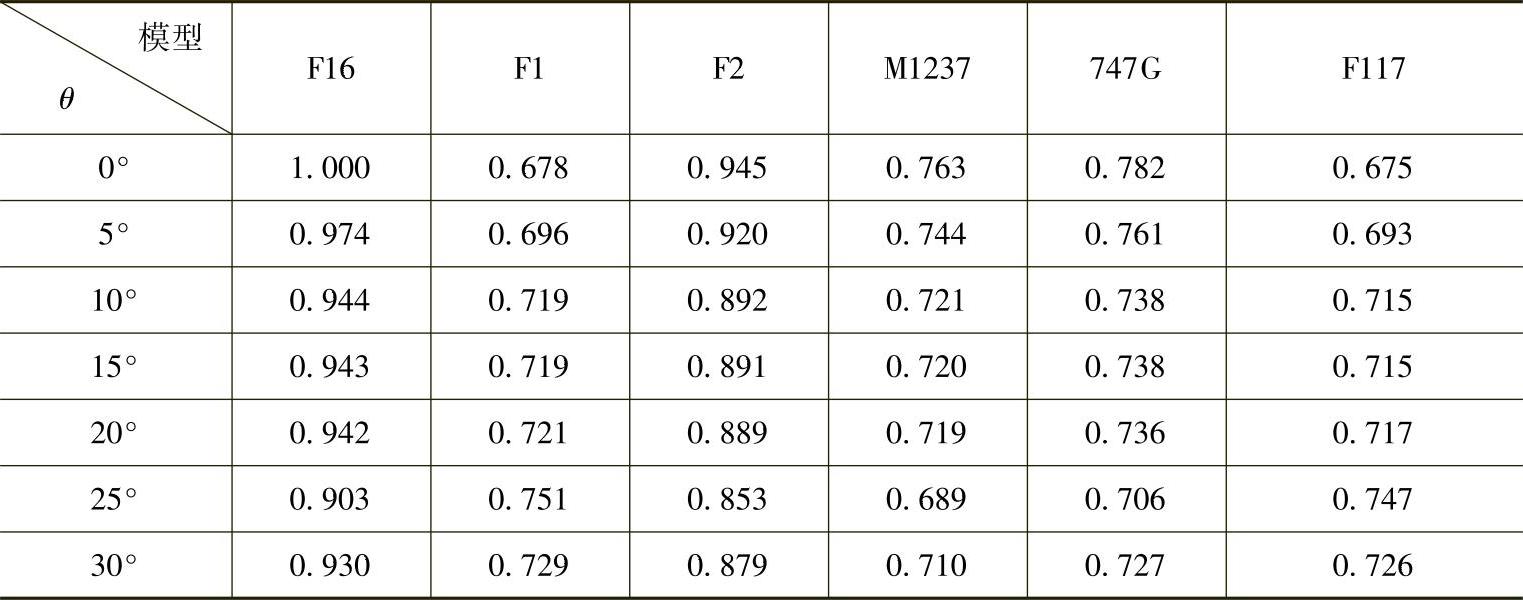
由实验结果可以看出，基准角点作为目标图像中最具有代表性、能简洁反映目标特征的角点，抓住了目标形状上最“本质”的特征。通过每个基准角点到重心点G的距离，也可以定义出一个具有平移、旋转、尺度不变性描述子。但在进一步应用中会发现，坦克、车辆等目标的基准角点很难定义，或者说各个角点的作用不像飞机有如此显著的差别。这就导致了这种特征描述子只能在特定目标（例如飞机）的识别中发挥作用。灵活性不强，也不具备对局部遮挡目标的识别能力。

实验2：基于主分量与Hausdorff距离的目标匹配

本实验为了验证基于主分量与Hausdorff距离的目标匹配算法的通用性和鲁棒性，将八个三维模型在不同视点下的投影图：在每个模型的单位球上，从北纬90°到北纬60°，纬度每隔5°、经度取固定值（与机身最长轴线垂直）进行一次投影，每个模型都得到7幅投影图，样本数量共计8×7=56。我们使用每个三维模型（如F117战斗机、汽车、坦克等）在基准视点的投影图作为模板，并通过F16战斗机的所有样本对其进行相似性度量。表7-2是F16战斗机投影图（不同视点下）与其他三维模型投影图（基准视点下）的Hausdorff距离，距离为0表示样本与模板完全吻合，距离越大则表示样本与模板越不匹配。

表7-2目标与各个模型的Hausdorff距离

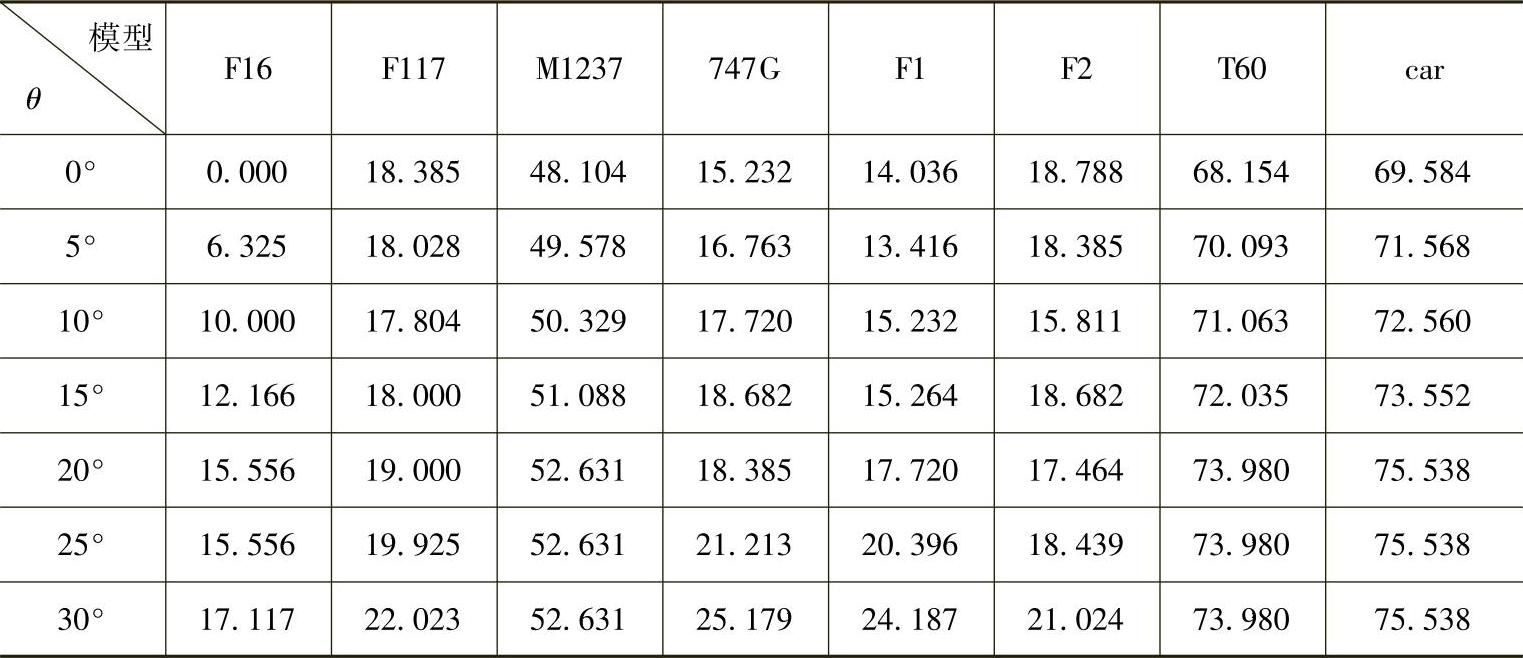
实验结果证明，基于主分量与Hausdorff距离的目标匹配算法能够很好地识别出不同类别的目标，即非常明显地区分出飞机和车辆，即使视点发生了高达30°的变化。但进一步对同类目标的识别效果相对逊色，比如，F16在基准视点与其在30°视点的投影图之间的距离显然要比F16与F1或F2在基准视点的投影图距离要大，这样就非常容易产生错误的匹配。可见，在视点发生变化的情况下，基于Hausdorff距离的目标匹配方法对于不同种类的刚性目标有着很好识别效果，而对同类目标的识别并不十分理想。

实验3：基于角点标记图与BP网络的目标分类

近年来，傅里叶描绘子、标记图和不变矩特征被广泛应用于目标识别领域。相对传统的矩形度、圆形度等描述方法，这三种特征不仅对复杂形状有着更好的逼真度，而且解决了平移、尺度和旋转不变性问题，基本上可以满足多数情况下形状匹配和目标分类的需求。但目标姿态变化导致的形状改变，是对传统的识别方法的新挑战，也对特征描述提出了更高的要求。

本实验将角点标记图与以上三种形状特征进行了实验对比，实验中使用相同的图像数据、同一种分类器——三层BP网络，特征向量的维数都为20（除不变矩的描述通常为7维）。选用的飞机3D模型为F16，F117，M1237，747G，在每个模型的单位球上，从北纬90°到北纬60°，纬度每隔5°、经度每隔2°进行一次投影，则在每个纬度下，共有360／2=180幅投影图，我们随机抽取其中的120幅作为训练集，余下的60幅为测试集。由于共有4个3D模型，每个模型在7个纬度下的进行投影，整个训练集和测试集样本数量分别为：120×7×4=3360，（180-120）×7×4=1680。作为基准视点，模型的正上方北纬90°对应于θ=0°的观察圆，北纬85°则对应与θ=5°的观察圆，以此类推。此处采用整个训练集的一部分数据对分类器进行训练，只是在基准视点（θ=0°）的投影图，共120×4=480幅。测试时用的是全部的测试集数据，即1680幅投影图。

实验结果如图7-11所示，两种角点标记图在视点发生变化的时候，对目标的识别效果好于其他三种特征。虽然在视角变化较小的时候（θ=5°），标记图的错误分类率小于角点标记图，但是当视角变化逐渐增大的时候，角点标记图的稳定性和识别率的优势愈加明显。

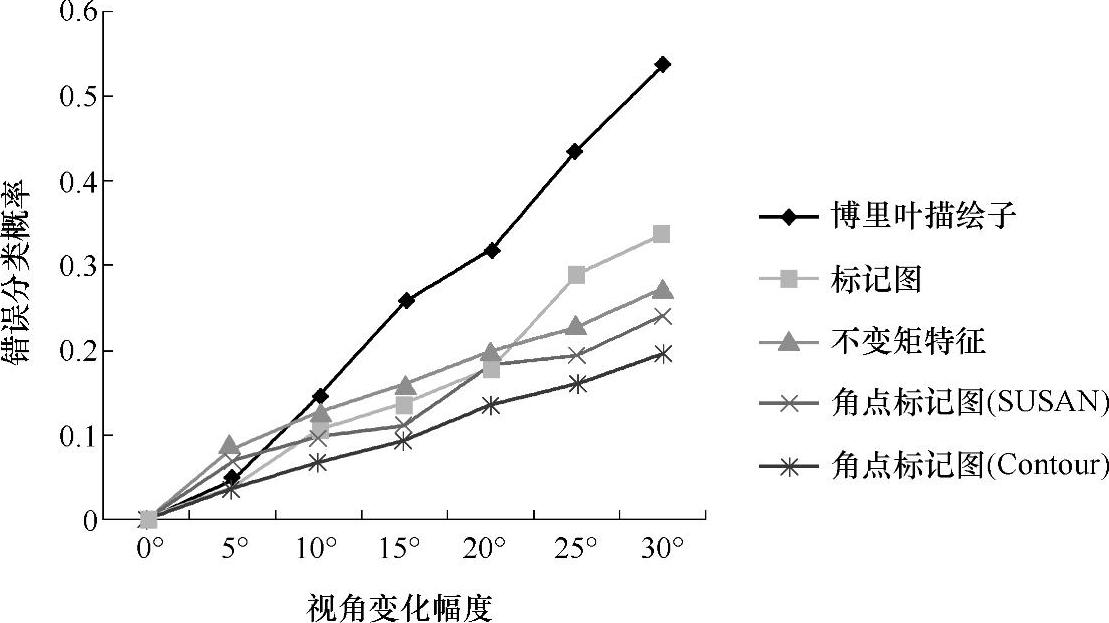
图7-11 五种特征在视点变化下的识别效果

实验4：增加训练模式后的分类效果改进

通过下面的训练方法尝试进一步提高系统的识别能力：在使用基准视点（θ=0°）的投影图进行训练之后，用余下的训练集数据对系统进行重新训练，再用新权值向量通过系统运行测试集样本来确立识别性能。图7-12给出了SUSAN角点特征通过持续这种再训练和令θ=5°，10°，15°，20°，25°和30°后进行的再测试过程得到的结果。

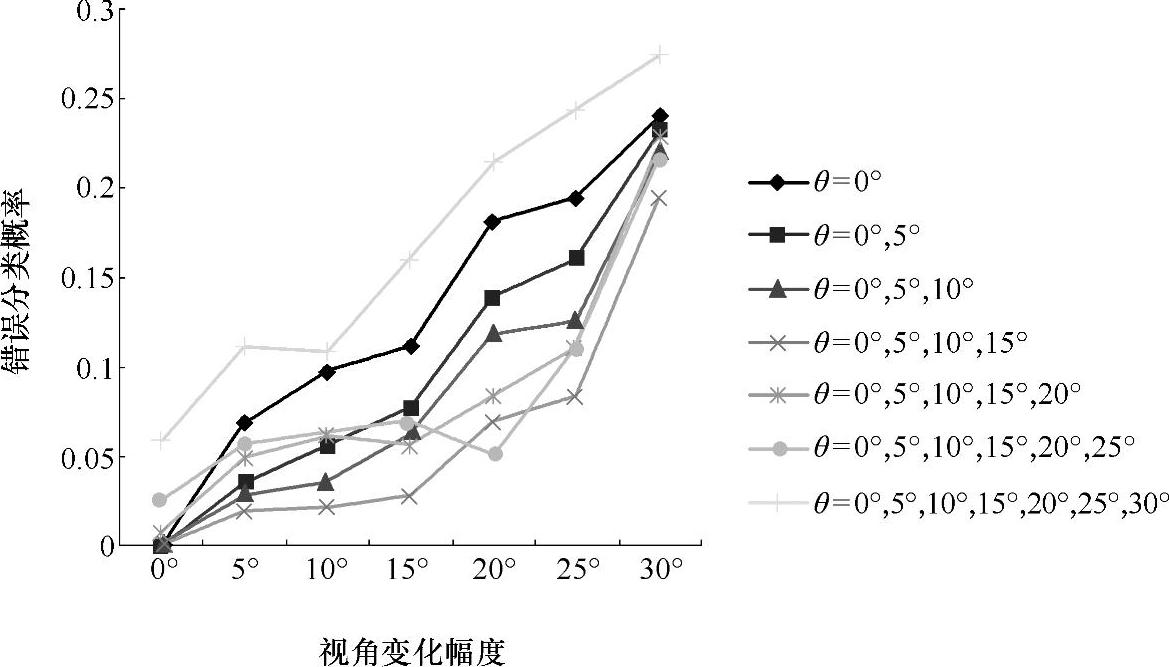
图7-12 通过增加训练模式改进识别效果

正如所希望的，如果系统进行了适当的学习，由测试集检测出的错误分类概率会在增大时降低，故通过系统性的、视点变化幅度小量增加的训练来增强系统的分类能力是很重要的。但如果视点变化幅度超过了15°，目标的形状变化剧烈甚至产生了自身的局部遮挡，这种情况下神经网络在学习过程中的收敛和稳定性就很不理想了。

使用特征和BP网络进行目标分类的实验研究

相关推荐