角点特征的技巧的分析介绍

2023-06-28 理论教育版权反馈

【摘要】：由于SUSAN算法不依赖于目标分割得到的轮廓信息，所以无法通过跟踪轮廓来得到角点的顺序，并依此计算每个角点的权重，进行特征空间的优化。两种角点检测算法及其相应的特征空间优化方法的效果，如图7-7所示。图7-7 对角点特征空间进行优化设计～e）是进行特征选择，g）～i）是进行特征的组合优化）

确定合适的特征空间是设计目标识别系统的一个十分关键的问题。如果所选用的特征空间能使同类物体分布具有紧致性，不同类别物体彼此分开，即各类样品能分布在该特征空间中彼此分隔开的区域内，这就为分类器设计提供良好的基础。反之，如果不同类别的样品在该特征空间中混杂在一起，再好的设计方法也无法提高分类器的准确性。对特征空间进行优化有两种基本方法，一种是特征选择，即对原特征空间进行删选，另一种就是特征的组合优化，即通过一种映射变换改造原特征空间。

通过对角点检测结果的仔细观察和分析，我们发现，过于密集的角点往往会局限于个例的细节变化，在训练分类器的时候容易产生过拟合现象。而且有一些点是图像获取或传输中产生的噪声，直接对目标的特征描述产生干扰。因此，为了减少分类器的训练复杂度、增强系统的鲁棒性，对特征空间进行适度的优化，是十分必要的。

对于直线投影法检测到的角点，按照在轮廓线上的顺序，如果一个角点与其前后两个角点的距离很近，且这三个相邻的角点和形心的距离相等或接近，则该角点所携带的信息与前后角点有冗余，可以删选掉。于是我们可以通过角点和质心的空间关系，计算出每个角点对于整个形状特征的重要程度，并据此对角点进行筛选：

式中，d_i表示第i个角点到形心的距离，D_i-1，i表示第i-1个角点和第i个角点（按照角点在轮廓线上的顺序）的距离，d_max是角点到形心的最大距离，D_max是相邻两个角点间的最大距离，ω₁和ω₂是该项的权重。

由于SUSAN算法不依赖于目标分割得到的轮廓信息，所以无法通过跟踪轮廓来得到角点的顺序，并依此计算每个角点的权重，进行特征空间的优化。但是，我们依然可以从角点负载信息量的角度考虑，将非常密集的角点群用一个点来代替，保留孤立、信息量巨大的角点，从而在优化特征空间的同时保持了目标的基本几何形状。

聚类分析是机器学习领域的一个重要研究方向，目前存在大量的聚类算法，算法的选择取决于数据的类型、聚类的目的和应用。本书选用凝聚的层次聚类方法^［128］对原特征空间进行组合优化，以求出一组对分类识别更为有效的特征。这种自底向上的策略首先将每个角点作为一个簇，然后将相似度最大的原子簇合并，直至达到某个希望的簇的数目。簇间相似度是通过计算平均相似度（一个簇中所有对象和另一簇所有对象之间的相似度的平均）得到的：

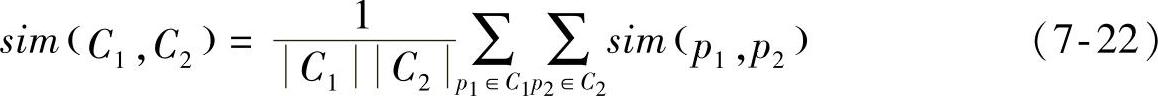
其中，相似度的度量采用的是欧氏距离。最终，用每个簇的重心（簇的所有角点的平均值）来代表整个簇。两种角点检测算法及其相应的特征空间优化方法的效果，如图7-7所示。

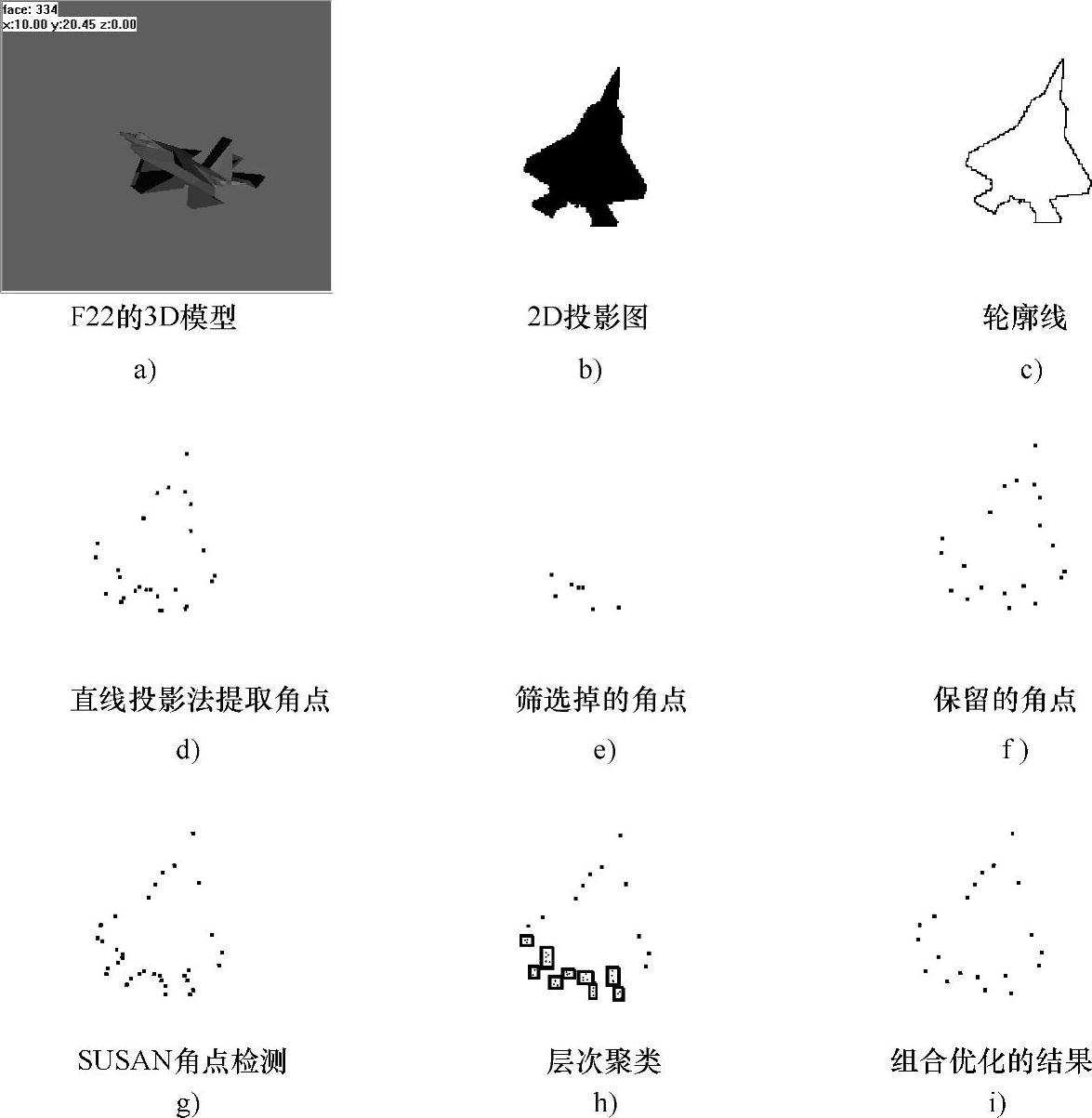
图7-7 对角点特征空间进行优化设计

（d）～e）是进行特征选择，g）～i）是进行特征的组合优化）

角点特征的技巧的分析介绍

相关推荐