1988年kass等人提出的基于能量函数的活动轮廓模型，即Snake模型，便是一种典型的自由式变形模板模型。Snake模型是一种有效地寻找目标轮廓的搜索算法，具有良好的提取、跟踪特定区域内目标边缘的能力，工作过程主要是利用能量最小化原理。实现Snake模型原型的算法通常十分复杂，曲线收敛速度慢且搜索范围有一定限制，因此许多学者提出了不同的算法，对经典Snake模型进行了改进。......
2023-11-24
基于主分量与Hausdorff距离的匹配算法
【摘要】：如图7-6所示，Hausdorff距离表征了两个点集之间的最大不相似程度。因为Hausdorff距离的适用形式限制在有限点集内，所以非常适合度量特征点集的相似性。而角点点集经过主分量法处理后，消除了其对尺寸、位置、方位的依赖性，就可以作为Hausdorff距离的匹配元素，对这些元素的相似性进行度量并将此度量值作为目标与原型相似性的依据，如此一来，大大降低了算法的运算复杂度，并减少了噪声对识别效果的影响。
霍特林（Hotelling）［207］提出了一个可以去掉一个随机向量中各元素间相关性的线性变换，并把它称作“主分量法”。此后，卡胡南（Karhunen）和列夫（Loeve）提出了一种针对连续信号的类似的变换。这种方法派生出了一种离散图像变换的方法。
我们根据角点的坐标可以生成二维向量，可以把这些二维向量当成原理中的随机向量X=(a，b)T处理，其中a和b是角点关于x1轴和x2轴的坐标值。总体的均值向量（边界点）可以通过K个样本向量（角点）来估计：
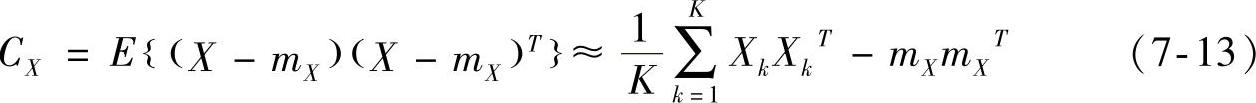
因为CX是实对称的，找到一组n个标准正交特征向量总是可能的。令ei和λi，i=1，2，…，n为特征向量和对应的CX特征值，以降序排布，使λj≥λj+1，j=1，2，…，n-1。令A为一个由CX的特征向量组成其行元素的矩阵，并进行排序，使A的第一行为对应最大特征值的特征向量，而最后一行为对应最小特征值的特征向量。假设把A作为将X的向量映射到用y代表的向量的变换矩阵，就得到了霍特林变换的表达式：
使用式（7-14）的实际结果是需要设置一个新的坐标系统，这个坐标系统以角点总体的质心（均值向量的坐标）为原点，以CX的特征向量所指方向为轴的方向，如图7-5b所示。这个坐标系统清晰地显示出式（7-14）所进行的变换是一种旋转变换，这种变换使用特征向量将数据排列起来，如图7-5c所示。实际上，这种排列正好是数据去相关的机理。另外，由于特征值沿着Cy的主对角线排列，λi是沿着特征向量ei的分量yi的方差，这两个特征向量是正交的。由于这个明显的原因，y轴被称为本征轴［8］。
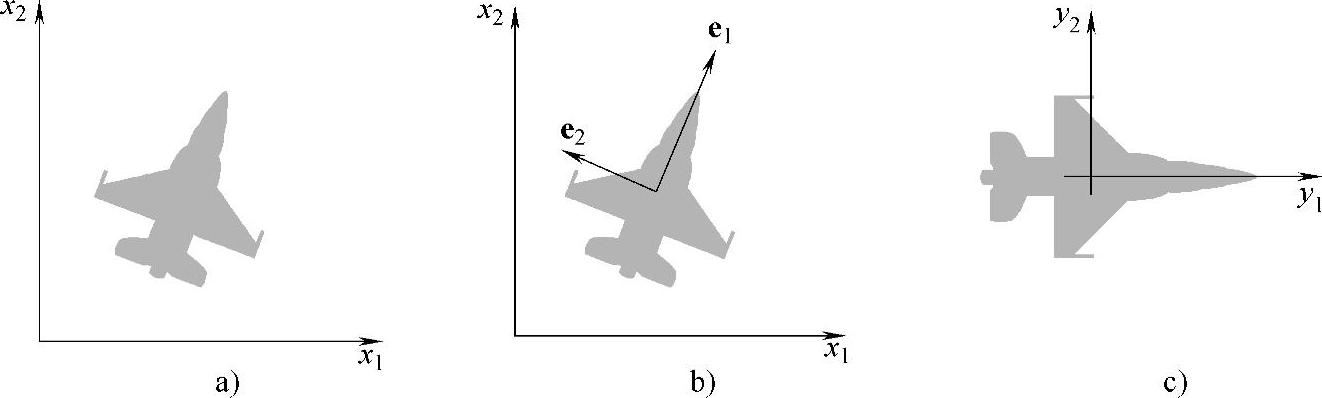
图7-5 用主分量法将目标沿着自身的本征轴对准
a）一个目标 b）特征向量 c）旋转目标
使用主特征向量排列角点的概念在图像描述中起着十分重要的作用。正如前面提到的，目标的描述对于大小变化、平移和旋转变化本应是尽可能独立的。使用目标的主轴校正的能力为消除旋转变化的影响提供了一种可靠手段。特征值是沿着本征轴的方差，并可用于尺寸的归一化。平移带来的影响可以通过将角点的均值设定为中心来解决。
Huttenlocher等人［208］提出的Hausdorff距离是用来描述两组点集之间相似程度的一种度量，是集合与集合之间距离的一种定义形式。它与许多其他匹配算法不一样，它并不要求目标与模板的简单一致，而是可以针对部分匹配作出良好的反应，因此它本身就具有一定的抗遮挡能力。对有限点集A=｛a1，a2，…，ap｝和B=｛b1，b2，…，bp｝，A，B之间的Hausdorff距离定义如下：
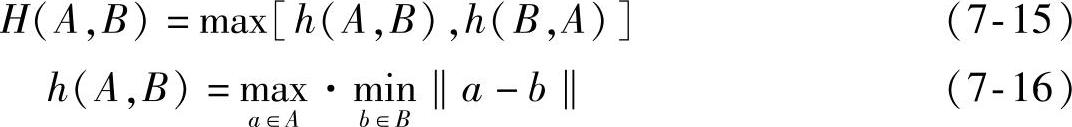
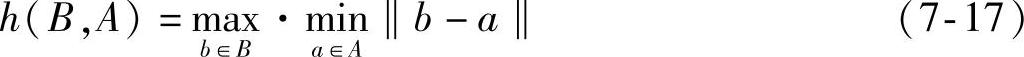
式中，H（A，B）是h（A，B）、h（B，A）中较大的那一个，称为A、B之间的Hausdorff距离；h（A，B）称为点集A到B的有向Hausdorff距离，即点集A中的每个点ai到B集中与其距离最近的点bj之间的距离ai-bj‖进行排序，取这样的距离中的最大值作为h（A，B）的值，同理可得h（B，A）；∗‖表示某种距离范数，如欧氏距离。如图7-6所示，Hausdorff距离表征了两个点集之间的最大不相似程度。
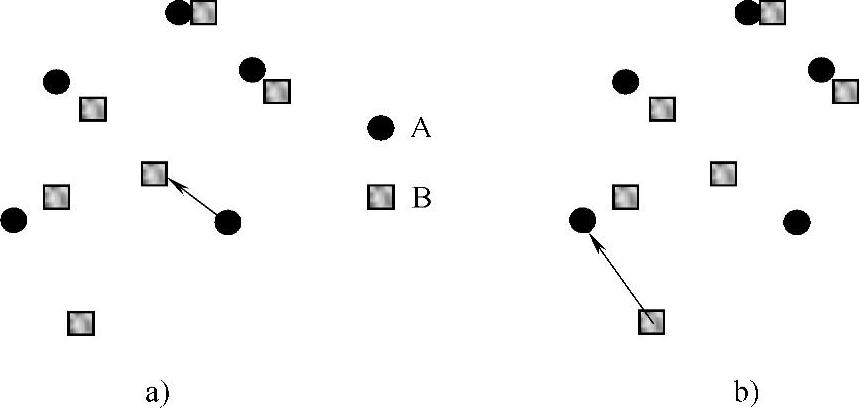
图7-6 Hausdorff距离示意图
a）表示点集A到B的有向Hausdorff距离 b）表示点集B到A的有向Hausdorff距离
在本书的应用中，为了降低噪声的影响，我们使用部分Hausdorff距离，其定义如下：
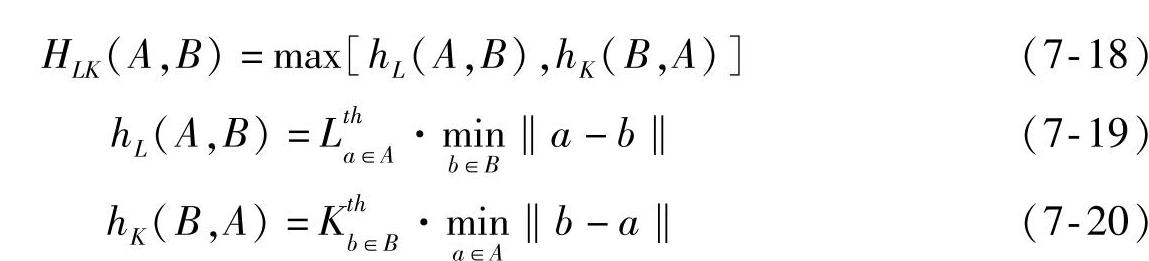
式中，HLK（A，B）仍是hL（A，B）和hK（B，A）中较大的一个。hL（A，B）虽然还是按照ai-bj‖（即A中的每个点ai到B中与其距离最近的点bj之间的距离）进行排序，但不是像h（A，B）那样取全局最大值，而是取第L个值（1≤L≤q，q为A集中点的数目），hK（B，A）同理可得。
通过角点检测算法可以得到待匹配目标和原型的两组特征点集，则目标匹配问题就转化为特征点匹配问题。因为Hausdorff距离的适用形式限制在有限点集内，所以非常适合度量特征点集的相似性。而角点点集经过主分量法处理后，消除了其对尺寸、位置、方位的依赖性，就可以作为Hausdorff距离的匹配元素，对这些元素的相似性进行度量并将此度量值作为目标与原型相似性的依据，如此一来，大大降低了算法的运算复杂度，并减少了噪声对识别效果的影响。
有关图像目标的表示与识别的文章
- 详细阅读
-
基于兴趣点的匹配算法在视觉测量技术中的应用详细阅读
此时，采用前述的外极约束能使整个匹配过程得以简化。不仅如此，上述两个特征点的幅值和方向也应该保持一致。进行匹配算法1）从左特征点图像的第iL行的现行列位置开始，找到下一个待匹配的特征点PLi。如果需要的话，也可引入顺序约束以进一步减少匹配运算。上述过程不断进行直到在右图像上找到具有最大一致性的特征点为止，并将其定为PLi的对应点PRi。显然，该PRi的列指标由jR指示。3）进行行终止检查。......
2023-11-24
-
基于NNDR的匹配策略的介绍详细阅读
对SIFT特征的研究［146］表明，可以通过比较最近邻特征和次近邻特征的距离可以有效地甄别局部特征是否正确匹配。这就是最邻近距离比值法，其表述如下，如果待匹配特征为DA，其最邻近特征为DB，次邻近特征为DC，那么判断该特征匹配的条件为：该方法理论来源是，如果一个特征在一幅图像中与两个特征的距离都很相近，那么该特征的区分度较低，也违背了Marr提出的“匹配应该满足唯一性”的原则，会对图像相似度的判断产生干扰。......
2023-06-28
-
基于原型匹配的反馈技术方案详细阅读
而基于内容的图像检索需要对一类物体进行匹配，比如检索有汽车、飞机、坦克、人群、楼房的图像，这种情况下就需要对具体的局部特征进行组合优化，从而得到对某类物体的理想化表征——原型。原型匹配理论是这样描述知觉加工的：当一种视觉系统收到一个新刺激，该系统就会将它与原先存储的原型进行比较，但并不要求完全相匹配，事实上大致的匹配就可以了［13］。为了实现从模板匹配到原型匹配的转变，我们引入了相关反馈技术。......
2023-06-28
-
基于Spark的聚类算法实现详细阅读
Spark MLlib中的K-means算法使用Map分布式读取数据集，并存储在内存里。计算时，用Map键值对表示随机挑选出来的k个聚类中心，Spark的驱动器节点负责把数据发送到各个工作节点，以实现具体的计算任务。Spark MLlib不同于传统的机器学习工具，它提供了简单易用的API，特别是Spark能够高效地处理大数据，并且在迭代计算时具有较强的优势。......
2023-11-21
-
基于模板匹配的检索方法的介绍详细阅读
这一模型意味着在我们的知识基础中，已经存储了数以百万计的不同模板——每一个可以辨识的不同物体或模式，都有一个与之匹配的模板存在。本书结合局部特征的特点和模板匹配的原理，提出了一种图像检索方法。如果局部特征和模板匹配的数量越多，则该幅图像和查询图相似的程度就越高。显然，模板匹配并不完全适合知觉原理的实际应用。......
2023-06-28
-
基于局部特征和原型匹配的图像检索技术详细阅读
现有的图像检索方式主要分为两种：基于文本的图像检索和基于内容的图像检索。针对以上两点问题，本书对局部特征提取技术和相关反馈技术进行了深入的研究分析，提出了一种基于局部特征的图像检索方法。......
2023-06-28
-
基于W-O算法的谱估计方法详细阅读
对于双窗系统，EN不再恒等于1，但具有“倒余弦”形状，这样W-O分析谱中在每点都产生旁瓣。同古典谱估计方法相比，由于AR模型是一个有理分式，因而估计出的谱比古典谱估计法估计出的谱平滑。由式易知，X0在k=0时的权值为N，即阶数越高，W-O谱线分辨力越强。图6-9 传统信号加窗与W-O谱分析由图6-9可以看出，用W-O方法得到的信号频谱比用传统加窗方法具有更少、更低的旁瓣干扰。......
2023-06-23
相关推荐