首页理论教育利用基准角点实现目标匹配

利用基准角点实现目标匹配

2025-09-29 理论教育版权反馈

【摘要】：对多维距离向量这种最具代表性的角点描述方法进行深入分析后，不难发现，数量繁多的角点不仅增加了运算时间，同时也给多帧图像中的目标匹配带来了困难，尤其是有噪声干扰和在目标姿态变化的情况之下。通过重心点G和P1可以得到飞机的一条基准轴线，显然，飞机两翼上的角点都位于这条轴线的两侧。

对多维距离向量这种最具代表性的角点描述方法进行深入分析后，不难发现，数量繁多的角点不仅增加了运算时间，同时也给多帧图像中的目标匹配带来了困难，尤其是有噪声干扰和在目标姿态变化的情况之下。为了达到更加高效、灵活的识别效果，本书希望能够选择出目标图像上最具有代表性的角点，根据这些基准角点的位置信息测量物体，并通过测量值来识别目标。

以军事目标飞机为例，测量一个飞机可以利用的最显著的信息就是机头部分、两翼部分和机尾部分的角点，以及它们和飞机重心的位置关系。飞机重心的计算公式如下：

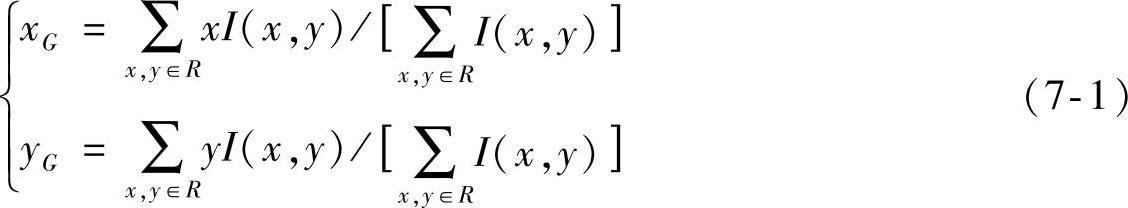
式中，(x_G，y_G)是重心点G的位置坐标，I（x，y）是像素点（x，y）的灰度值。我们可以通过计算每个角点的相对重心的重心矩，并选择重心矩最大的角点作为第一基准角点P₁（x_p1，y_p1）：

式中，C为角点点集，其包含的角点数目为n。

通过重心点G和P₁可以得到飞机的一条基准轴线，显然，飞机两翼上的角点都位于这条轴线的两侧。于是这条轴线就把机翼角点点集划分为两个子集：

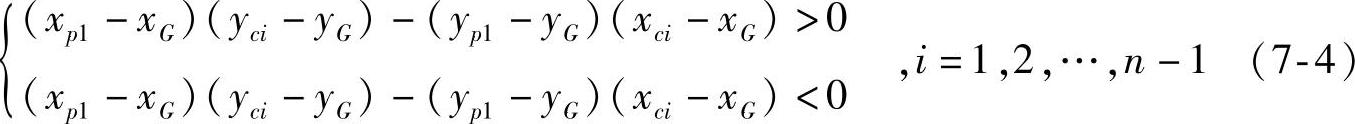
而两翼上的基准角点就可以定义为距离这条轴线最远的点——第二基准角点P₂（x_p2，y_p2）和第三基准角点P₃（x_p3，y_p3）。角点与基准轴线的距离可以由以下公式计算得到：

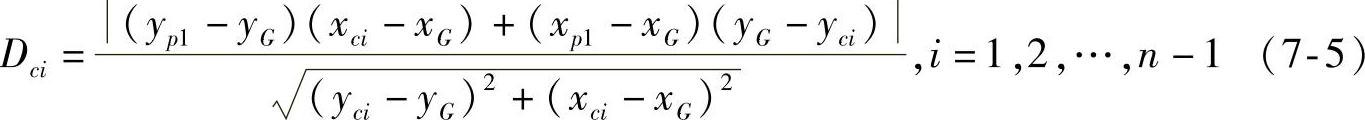
第四基准角点P₄（x_p4，y_p4）被定义在机尾，它和第一基准角点P₁分别位于基准轴线的两端，也就是重心点G的两侧。如果P₁满足以下条件：

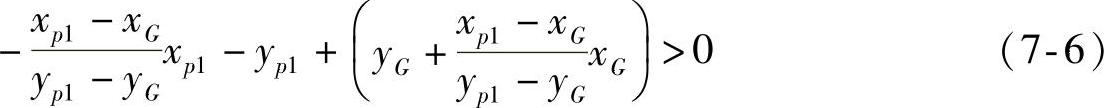(https://www.chuimin.cn)

则P₄将满足

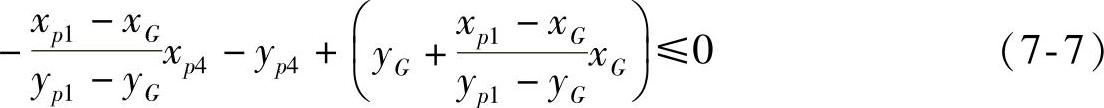
否则，必然有

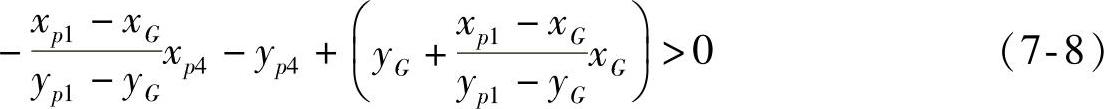
在目标识别过程中，特征空间优化的目的是用最少的描述获得目标形状上最“本质”的特征。通过每个基准角点到重心点G的距离，可以定义出一个区分度较高的描述子：

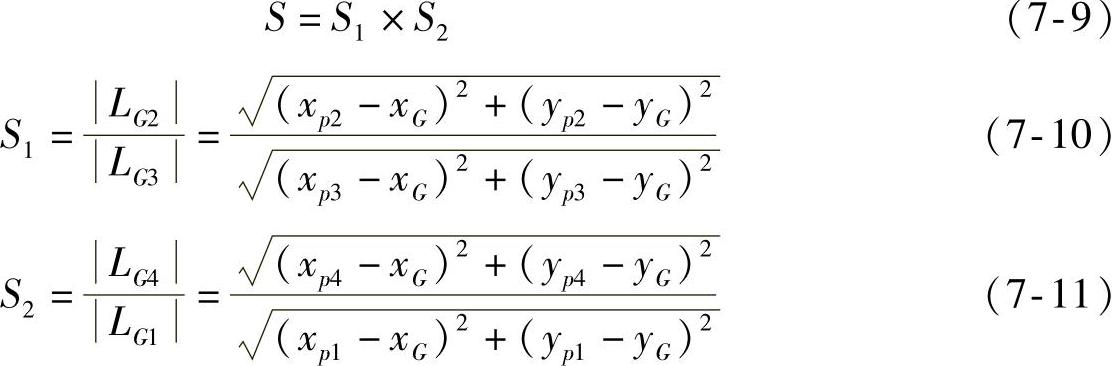
如图7-4所示，用SUSAN算法检测出了F16战斗机图像的所有角点，并按照上述方法获得了四个基准角点，从而构造出了特征描述子S。

图7-4 飞机图像的基准角点提取

a）F16战斗机 b）角点（SUSAN） c）4个基准角点