多分辨率图像配准的方法介绍

2025-09-29 理论教育版权反馈

【摘要】：以多分辨率来解释图像的一种有效但概念简单的结构就是图像金字塔［8］。图5-6 基于多分辨率技术的图像配准为了实现图像序列的拼接，就必须确定有重叠的两幅相邻图像的空间对应关系，这也是图像拼接中关键的一步。3）投影变换：如果一幅图像上的直线经过变换后映射到另一幅图像上仍然为直线，但平行关系基本不保持，则这种变换称为投影变换。

图像配准也称图像对齐，是对从不同传感器或不同时间或不同角度所获取的两幅或多幅图像进行最佳匹配的处理过程。而图像配准的本质是寻找一种图像对之间的变换关系，在这种变换关系下，两幅图像之间可以建立像素点之间的对应关系。经过多年发展，人们提出了许多种图像配准的方法^{［174，182，183］}，大体可以分为三类。

1.基于频域的方法

基于频域的方法，即相位相关法。它是利用傅里叶变换将两幅待配准的图像变换到频域，然后利用它们的互功率谱直接计算图像的变换关系，从而完成配准。其优点是算法简单，效果理想，图像存在的平移、旋转、仿射等变换关系会在傅里叶变换域上有相应的体现，所以该类方法具有一定的鲁棒性。拼接的前提条件是待拼接图像之间重叠区域比例大，一般要求超过50％，这使得其在实际运用受到较大限制。

2.基于区域的方法

基于区域的方法，即灰度相关法。它是计算图像之间重叠区域对应灰度的统计信息，然后根据特定的相似度量为配准准则。该类方法实现简单，但是应用范围非常狭窄，不能用于非线性变换，而且运算量大。

3.基于特征的方法

提取图像的局部特征信息，运用特定的相似度量实现配准。由于图像特征种类非常多，有特征点、边缘、轮廓、闭合区域、统计特征等，相对于其他方法，基于特征的方法运算速度较快，能够容忍较大的图像差异，获得的配准结果比较稳定，已经成为当前主流的图像配准方法。

当前已有的基于特征的图像配准方法普遍存在一个问题：它们提取的特征稳定性较差，通常不具备对仿射或透视投影变换的不变性，难以适用于成像情况相对复杂的航拍图像。近年来，在工程应用中发现，局部特征不仅对图像尺度、平移、旋转变换具有不变性，而且对光照变化以及复杂的投影变换也具有部分不变性，比较适合用于航拍图像序列的处理，在图像场景较大、天气和飞行器姿态的影响普遍存在的情况下，可以实现准确、稳健的航拍图像配准。

许多国内外文献，如参考文献^{［143，144，146］}都曾指出，在复杂内容的图像中提取的特征点非常多，过多的特征点不仅会加重计算负担，影响效率，而且会对特征匹配造成干扰，不利于航拍图像序列的准实时拼接。本书的拼接方法只需利用少量（3个以上）特征点即可完成图像配准，这对特征点的提取质量提出了较高要求，而多分辨率分析就为解决这个问题提供了一条有效的途径。

当观察图像时，通常看到的是相连接的纹理与灰度级相似的区域，它们相结合形成物体。如果物体的尺寸很小或对比度不高，通常采用较高的分辨率观察；如果物体尺寸很大或对比度很强，则只需较低的分辨率。如果物体的尺寸有大有小，或对比度有强有弱的情况同时存在，以若干分辨率对它们进行研究将具有优势。这就是多分辨率处理的魅力所在，而且这样由粗糙到精细的分析策略在模式识别中可以发挥出很大的作用。

以多分辨率来解释图像的一种有效但概念简单的结构就是图像金字塔^［8］。图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔就是一系列以金字塔形排列的分辨率逐步降低的图像集合。如图5-5所示，金字塔的底部是待处理图像的高分辨率表示，顶部是低分辨率的近似。当向金字塔的上层移动时，尺寸和分辨率降低。因为基础级J的尺寸是2 ^J×2 ^J或N×N（J=log₂N），所以中间级j的尺寸是2 ^j×2 ^j。完整的金字塔由J+1个分辨率级组成，由2 ^J×2 ^J到2⁰×2⁰，但大部分金字塔只有P+1级，其中j=J-p，…，J-2，J-1，J且1≤P≤J。也就是说，通常限制它们只使用P级来减少原始图像近似值的尺寸。

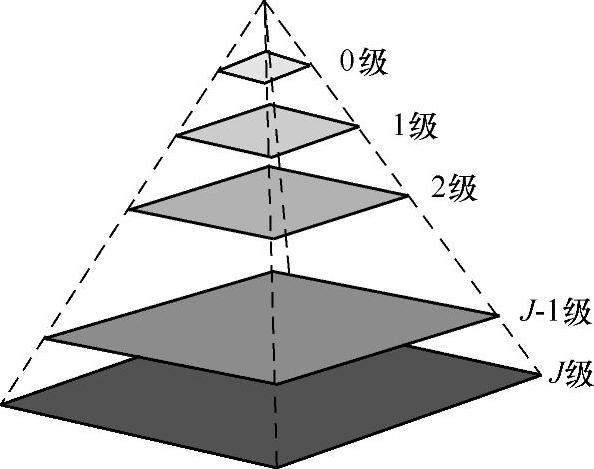
图5-5 图像金字塔的结构

如图5-6所示，由于从机载摄影器材上获取的图像分辨率较高，本书通过建立图像金字塔来降低待匹配图像的分辨率，在低分辨率的图像序列上提取出更具代表性的特征点对，并计算出这些特征点在原始图像中的位置从而进行图像变换。

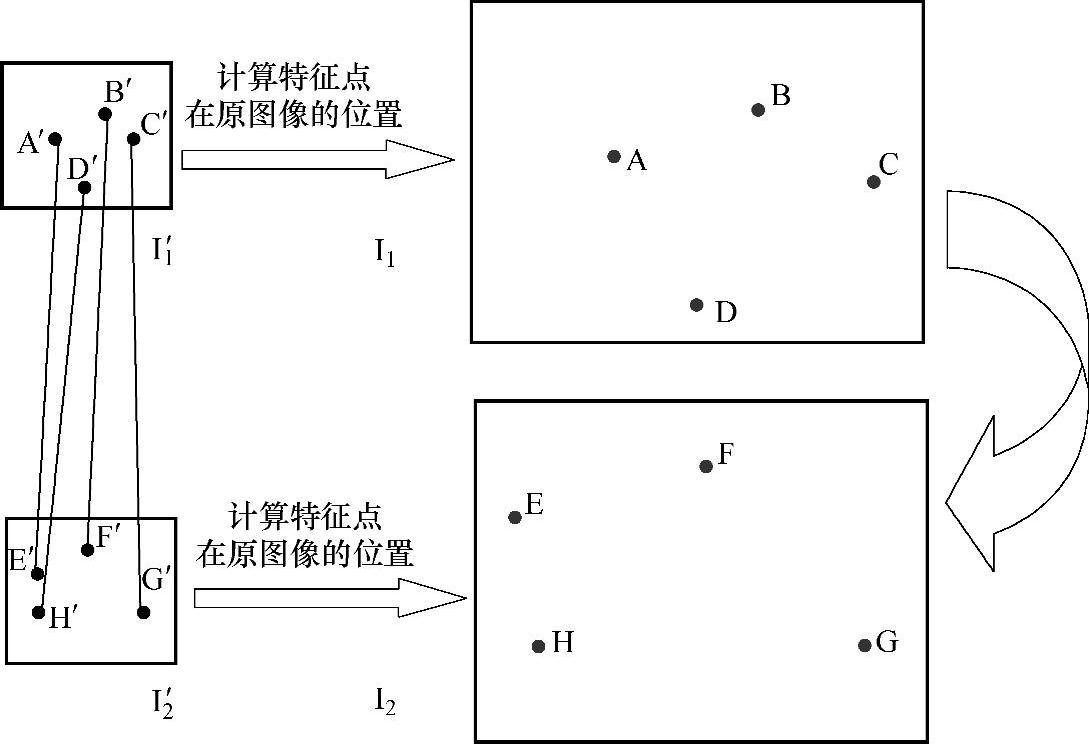
图5-6 基于多分辨率技术的图像配准

为了实现图像序列的拼接，就必须确定有重叠的两幅相邻图像的空间对应关系，这也是图像拼接中关键的一步。为了确定图像间的对应关系，需要清楚相机进行图像采集时的运动方式，因为相机不同的运动方式会对场景成像产生不同效果，如图5-7所示。(https://www.chuimin.cn)

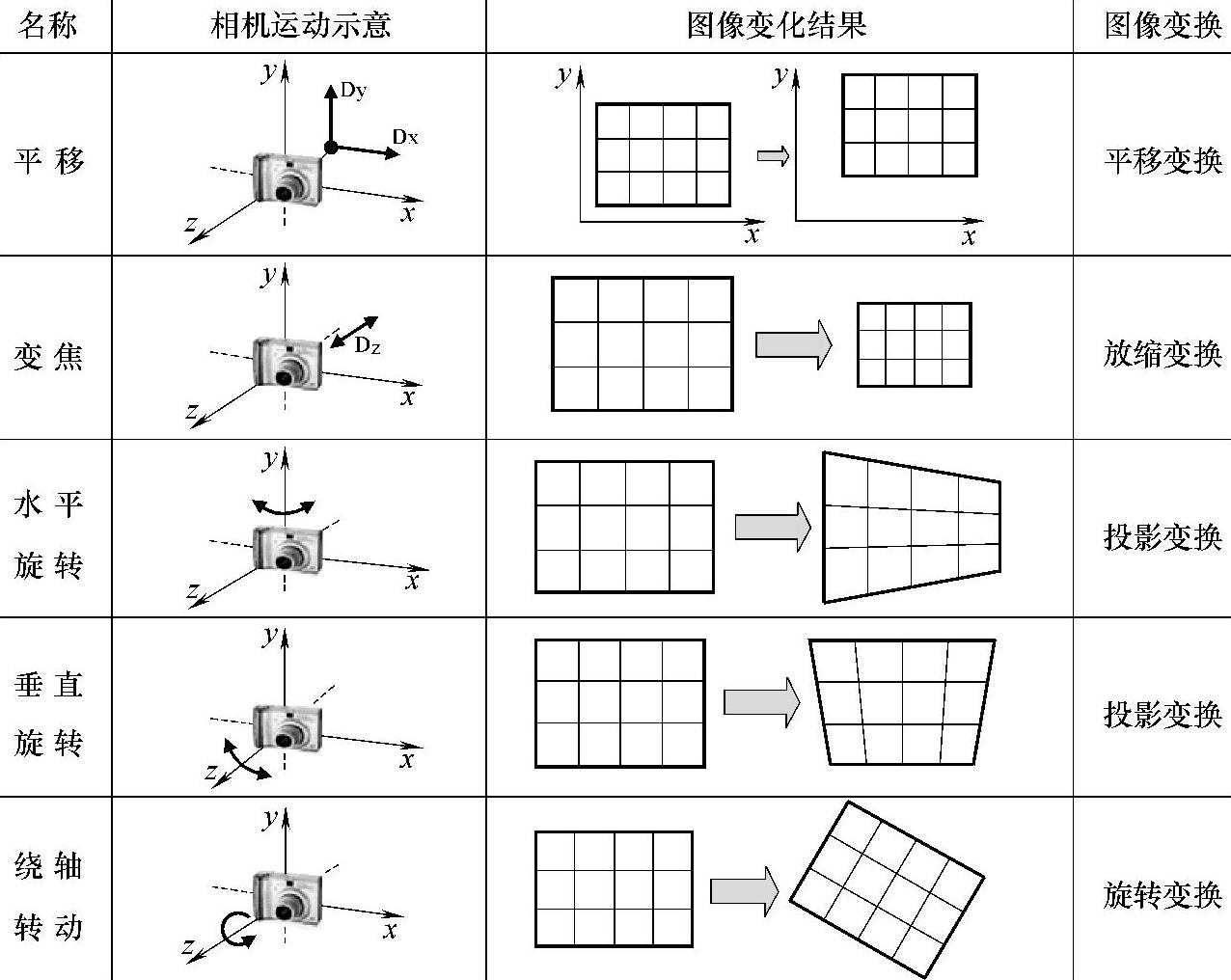
图5-7 相机的运动方式与成像结果之间的关系

一旦确定了图像间的关系模型，则图像之间的配准问题就转化成确定该模型的参数问题。目前常用的关系模型有刚性变换（Rigid Transform）模型、仿射变换（Affine Transform）模型、投影变换（Projective Transform）模型以及非线性变换（Nonlinear Transformation）模型等。

1）刚性变换：如果一幅图像中的两点间的距离经变换到另一幅图像中后仍然保持不变，则这种变换称为刚性变换。刚性变换只局限于平移、旋转和反转（镜像），不会扭曲物体的原有形状，其变换矩阵具有3个自由度。

2）仿射变换：如果一幅图像上的直线经过变换后映射到另一幅图像上仍然为直线，并且保持平行关系，则这种变换称为仿射变换。仿射变换描述摄像机的平移、旋转、缩放运动。其变换矩阵具有6个自由度。

3）投影变换：如果一幅图像上的直线经过变换后映射到另一幅图像上仍然为直线，但平行关系基本不保持，则这种变换称为投影变换。投影变换具有更一般的形式，可以描述摄像机的平移、水平扫动、垂直扫动、旋转、镜头缩放等运动，其变换矩阵具有8个自由度。它适用于景物平面相对于像平面有一定倾斜的情况，刚性变换模型和仿射变换模型可以看做是投影变换模型的特例。

4）非线性变换：非线性变换，也称为弯曲变换。经过非线性变换，一幅图像上的直线映射到另一幅图像上不一定是直线，可能是曲线。多项式变换是典型的非线性变换，如二次、三次函数及样条函数，有时也使用指数函数。

理论上讲，在图像变换的时候考虑的参数越多，得到的结果越精确。但在实际应用中，由于飞行器飞行轨道的起伏、地面物体高度的变化等因素，参数过多的变换矩阵反而起到的放大误差的效果，并且需要至少7个特征点对才可以进行配准。

通过对实际数据的研究，我们发现航空拍摄平台通常距离地面较远，可以将一定范围内的大地场景近似看成一个平面区域，这样一来就能够把一定长度的航拍图像序列变换到同一个成像平面完成图像配准。在各种图像变换模型中，虽然投影变换的描述能力更强，但依据奥卡姆剃刀（Occam's Razor）定律^[1]，本书针对航拍图像的特点采用了仿射变换模型。该模型可以描述图像的旋转、平移和缩放等运动，利用3个以上特征点即可完成图像拼接，不仅极大简化了计算，拼接的最终效果也能够达到相应要求。

设成像平面上某一点P_i的坐标为(x_i，y_i)，其三维齐次坐标为(x_i，y_i，1)。设一个观测点在两个相邻帧图像上所成的像点分别为P₁和P₂，则这两点的齐次坐标之间满足如下关系：

P₂=TP₁ （5-5）式中，T为8参数投影变换矩阵。实验证明，由于航拍图像序列中相邻两帧图像间视差较小，可以用式（5-6）给出的仿射变换矩阵来近似表达式（5-5）中的T，这样也有效地简化了计算。

根据线性方程相关理论，至少需要3个特征点对才能对这个6参数的仿射变换矩阵求解。但实际应用中，我们提取的特征点对数量通常大于3，这时可以利用最小二乘法估计仿射变换矩阵T，相应的误差为

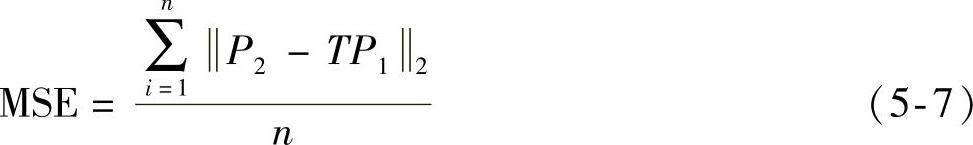
判断图像配准的结果优劣的标准与其应用的领域有关系。比如，在军事制导领域，图像中目标定位的精确度与算法的速度是最重要的；在医学领域，获取的图像简单而正规，就可以采用比较简单的模板匹配；在卫星遥感方面，可以采用已知位置的标定物来定位配准。可见，图像配准本身就具有多样性和特殊性，在这几十年的技术发展过程中，还存在许多问题。图像配准的精度和效率上很难找到一个通用的平衡点，其针对性较强，自适应性不足，限制了图像拼接的实际应用范围。

多分辨率图像配准的方法介绍

相关推荐