基于霍夫变换的目标检测算法

2025-09-29 理论教育版权反馈

【摘要】：基本的霍夫变换最初是用来进行直线检测的，而广义霍夫变换则可以在所需检测的曲线或目标轮廓没有或不易用解析表达式时，利用表格来建立曲线或轮廓点与参考点间的关系，进而检测出目标［67］。霍夫变换的突出优点就是可以将图像中较为困难的全局检测问题转换为参数空间中相对容易解决的局部峰值检测问题。

一幅图像往往可以提取出超过2000个局部特征，而这些局部特征很可能来自场景中的多个物体或背景。如何从这些特征中寻找到只属于待识别目标的局部特征子集，这是进行目标匹配识别所必须解决的问题。霍夫变换（Hough Transform）为此提供了一条高效的途径。

基本的霍夫变换最初是用来进行直线检测的，而广义霍夫变换则可以在所需检测的曲线或目标轮廓没有或不易用解析表达式时，利用表格来建立曲线或轮廓点与参考点间的关系，进而检测出目标^［67］。霍夫变换的基本思想是将原图像变换到参数空间，用大多数边界点满足某种参数形式来描述图像中的线，通过设置累加器进行累积，求得峰值对应的点所需要的信息。霍夫变换以其对局部缺损的不敏感，对随机噪声具有鲁棒性以及适于并行处理等优良特性，备受图像处理、模式识别和计算机视觉领域学者的青睐。霍夫变换的突出优点就是可以将图像中较为困难的全局检测问题转换为参数空间中相对容易解决的局部峰值检测问题。

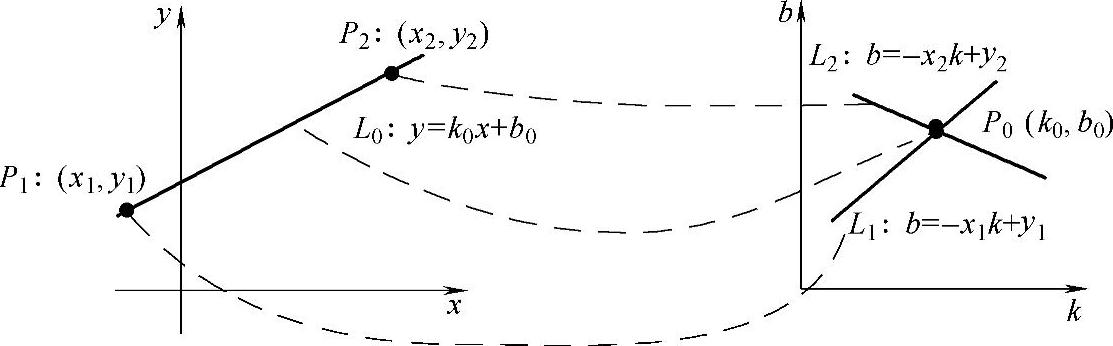
图5-3 直线检测中的霍夫变换

霍夫变换利用点线对偶性原理进行坐标变换，原理如图5-3所示，在直角坐标系下，利用公式（5-2）表示过点（x，y）的直线L₀的方程：

y=k₀x+b₀ （5-2）

式中，k₀为斜率；b₀为截距。将其变换为参数空间中过点（k₀，b₀）的直线方程：

b₀=-xk₀+y （5-3）(https://www.chuimin.cn)

可以看出，直线L₀上的两个点（x₁，y₁）和（x₂，y₂），在参数空间中表示为两条直线不同的直线L₁和L₂，而它们在参数空间中相交于（k₀，b₀）点。也就是说，原图像空间中同一条直线上的不同点在参数空间中被变换为一组相交于同一点的直线。

使用公式（5-2）表示一条直线带来的一个问题是，当直线接近垂直时，直线的斜率接近无限大。解决这一难点的一种方法是使用极坐标方程来表示直线：

ρ=xcosθ+ysinθ （5-4）其中ρ为原点到直线的距离（即原点到直线的垂直线的长度），θ确定了直线的方向（即原点到直线的垂直线与x轴方向的夹角）。如果对位于同一直线上的n个点进行霍夫变换，则原图像空间中的这n个点在参数空间中对应得到n条正弦曲线，并且这些曲线相交于同一点了，若能确定参数空间中的P₀点（局部最大值），也就实现了直线的检测。

本书对目标姿态建立一个参数空间，将目标的2D坐标、尺度、方向参数等坐标轴按照一定的步长划分为若干等份；然后将所有匹配的特征点向这个参数空间投票；对参数空间每个点的投票累加值进行分析，累加值大的点所对应的目标姿态有更高的概率出现在图像中。在实际应用中，对于参数空间坐标轴步长，一般2D坐标为训练集中目标最大尺寸的0.25倍，尺度因子为2，方向参数为30°。累加值和预设的阈值进行比较，当大于阈值时，则判定该点所对应的目标姿态存在于图像中。

在图5-4中，左图所示的两个目标——玩具火车和玩具青蛙，由于其他物体（包和箱子等）的存在，在中间的图像里都产生了局部遮挡，而采用上述的目标匹配方法都可以将这些目标识别出来，识别效果图如右图所示。大的矩形框中是识别出的目标，小的矩形框代表识别所用到的局部特征。

图5-4 局部遮挡目标检测(来源：Lowe,2025年)

基于霍夫变换的目标检测算法

相关推荐