用穷举法搜寻最邻近点以及次邻近点，可以得到最精确的结果。但是由于本书所用的特征空间一般都高达128维以上，加之复杂图像的局部特征数量比较多，搜索算法的效率显然成为了整个系统的一个瓶颈。
1.K-D树搜索策略
标准K-D树是Friedman等人［178］提出的一种高维二叉树，K表示空间的维数，在其上可实现对给定特征点的快速最近邻查找。若某K-D树的结点数目为N，则在它上面的最邻近节点的平均计算复杂度为O（lgN）。其后又相继提出了K-D树的1+ε近似最近邻搜索算法（ANNS），其主要思想是在搜索时只查询那些与给定特征点的距离小于当前最近距离1／(1+ε)倍的点，此时搜索完成时返回的点未必是真实的最近邻点（除非ε=0），但是即使当ε取的较大（如ε=3时），所返回的点仍然有50％的机会是真实的最近邻点，而且在平均意义上它们到目标点的距离只是真实最近邻点到目标点的距离的11.5倍，取得的加速比却可以达到50倍以上。
在数据维数较低的时候，K-D树搜索方法比较有效。在更高维的数据空间中将会有更多的分类结果接近目标真实数据，此时使用K-D树进行搜索的话，效率将会急剧下降。本书所用的特征空间一般都高达128维以上，为此本书使用了Beis和Lowe提出的Best-Bin-First（BBF）算法［146］，它对常规的K-D树搜索方法进行改进，从而实现较快的匹配点搜索。
2.基于BBF算法的搜索策略
在高维数据搜索空间中，K-D树搜索的结果仅仅只有很少的一部分满足邻近原则，为了加快搜索速度，可以通过减少搜索节点来缩小搜索范围。这需要使用一个基于堆的优先级队列，将搜索空间的节点按照与待查询节点的距离来进行排序。当搜索到的节点符合设定的约束条件，则记录到优先级队列中去，从而获取下一个候选节点的信息（包括该节点在当前树的位置和到待查询节点的距离）。当一个最邻近点被搜索到后，则从队列的队首删除一项，然后继续搜索包含最近邻节点的其他分支。
如图5-2所示，对于特征点数量达到10000、维度为5～25的数据检索中，按照BBF算法改进的搜索策略很大程度上提高了检索效率，而标准的K-D树搜索策略在数据维度达到10后其效率便明显下降了。
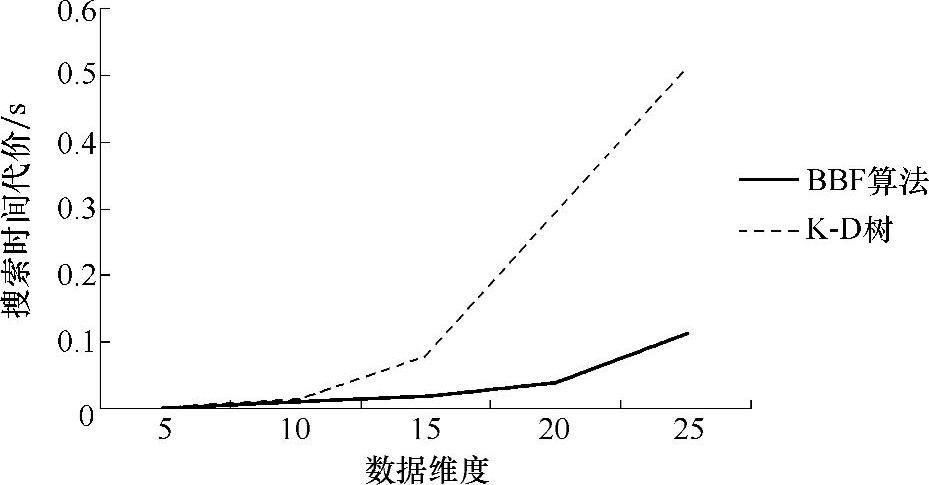
图5-2 BBF算法与K-D树的搜索时间代价
本书设定的约束条件是检查前200个最邻近候选节点，该算法在搜索速度提高了2个数量级的同时，平均只丢失5％的特征对，这对于一般的图像检索来说是可以容忍的。当距离非常相近的特征点需要进一步甄别的时候，BBF算法的搜索效率会受到制约，但是本书剔除了与最近邻点和次近邻点距离比值大于0.8的特征对，这就基本上避免了这一困境。
有关图像目标的表示与识别的文章
图4.3.45 创建基准曲线3图4.3.46 截面草图Step7.创建扫描混合特征。创建图4.3.47所示的扫描混合特征，相关操作如下：选择下拉菜单命令，系统弹出图4.3.48所示的“扫描混合”操控板，在操控板中按下“实体”类型按钮。图4.3.47 创建扫描混合特征图4.3.48 “扫描混合”操控板定义扫描轨迹。②在系统的提示下，单击图4.3.51中的圆弧。图4.3.52 “链”对话框图4.3.53 选择起始点定义第二个混合截面。图4.3.58 抽壳特征Step10.创建图4.3.59所示的PNT1基准点。......
2023-06-20
图4.1.15a所示的模型，有两个特征，现需对拉伸特征的表面进行拔模，该拔模面势必会遇到旋转特征的边。此时如果在操控板中选择了合适的选项和拔模角，可以创建图4.1.15b所示的延伸相交拔模特征。图4.1.15 拔模特征的延伸相交Step1.将工作目录设置至D：\proewf5.2\work\ch04.01，打开文件draft_extend.prt。图4.1.16 选取拔模面图4.1.17 选取拔模枢轴平面图4.1.18 拔模参照平面Step6.在操控板的“选项”界面中选中复选框，如图4.1.19所示。Step8.单击操控板中的按钮，完成特征的创建。......
2023-06-20
利用互信息法选择特征的基本原则是选择类别相关的特征，同时排除冗余的特征。因此，基于互信息的特征选择一般遵循这样一种模式：在顺序前向搜索中寻找与类别互信息最大而与前面已选特征互信息最小的特征项。在目标分类中可以简单认为：互信息越大，特征ti和类别Cj共现的程度越大。那么，ti和Cj的互信息可以由下式计算：式中，A、B、C、D的含义和6.4.3节中约定的完全相同。......
2023-06-28
a称为A 点在H 面上的正投影，即水平投影；a′称为A 点在V 面上的正投影，即正面投影。让V 面不动，把H 面向下转动90°，把V、H 两面投影体系展开，可得展开后点的两面投影，如图2-19 所示。在投影图中，点用小圆圈表示。图2-19点的两面投影显然，有了点的两面投影图，点在空间的位置能被唯一确定。综上所述可总结出点的两面投影的投影规律。点与其投影的连线垂直投影轴。空间点到V 面的距离等于水平投影到OX 轴的距离。......
2023-06-22
由于口吃者有言语不流畅的异常特征，因此这种不流畅的发生频率和严重程度较一般人来得高。在停顿发生时，口吃者的声门时常会关闭，造成声带无法发生振动。波动性可因人而异。......
2023-07-02
图3-16力对点的矩实例脚蹬自行车；羊角锤拔钉子；开、关门；扳手拧螺母由经验可知，力的这种转动作用不仅与力的大小、方向有关，还与转动中心至力的作用线的垂直距离d 有关。互成平衡的两个力对于同一点的矩的代数和等于零。......
2023-06-19
显而易见，在不同的参考物体上所观察的物体运动是不相同的。显然，牵连运动的类型与刚体运动类型一致。点或刚体的绝对运动是它们相对于动坐标系的相对运动与动坐标系相对于静坐标系的牵连运动的合成结果。研究运动的分析和合成问题，首先要选择好合适的静坐标系和动坐标系，然后分清什么是绝对运动、相对运动和牵连运动；最后分析各种运动的速度和加速度。......
2023-06-19
教学活动个性化，是教师教学艺术的独特标志。课堂教学是一个百花齐放的艺术园地，其功能在于促进学生主体性的发展，在于培养学生的创新意识和由“苦学”向“乐学”的转变。创造性教学所强调的交流与沟通包括两方面，一是师生间的，二是学生内部的。......
2023-07-19
相关推荐