通过支持向量机和程序实现了服装面料图像低层特征和三个因子之间的映射。本章在提出利用支持向量机作为面料图像情感因子和低层特征之间映射关系模型的基础上，对基于内容的服装面料图像情感语义识别和检索的框架进行了研究，并利用程序开发了面料图像样本数据管理的系统，实现了面料图像低层特征的提取以及利用程序实现了服装面料图像低层特征和三个情感因子之间的映射。......
2023-08-23
线矩特征描述子：一种有效的图像特征提取方法
【摘要】：如第2章2.3.3节所述，面矩作为一种全局信息，已经广泛用于完全分割后的目标识别，其具有前面所述的整体特征的优缺点。当对边缘曲线进行尺度变化时，尺度的变化导致曲线长度的变化，相应的变化因子是k。此时尺度变化后的中心矩成为μ′pq=μpq×kp+q+1。为此，对7个不变矩进行如下修正，以调整其取值范围：式中所进行的修正变换应综合考虑不变矩特征的大小及后续识别的结构特点。
如第2章2.3.3节所述，面矩作为一种全局信息，已经广泛用于完全分割后的目标识别，其具有前面所述的整体特征的优缺点。而针对图像边缘计算的不变矩，我们称之为线矩，作为一种局部特征，它主要利用目标图像的高频信息部分——边缘信息完成对图像的分析与理解［168］。由于通常目标边缘像素点的个数约为目标所有像素点的平方根，所以，用目标边缘像素来表示其形状要比用目标区域内所有的像素点少得多。
设数字图像中的边缘曲线由N个离散点组成，即(xi，yi)，i=1，2，…，N，则p+q阶线矩的定义为
式中，
相应的p+q阶中心矩定义为
式中，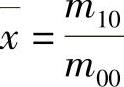
，
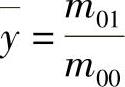，点(x，y)即为边缘的质心位置。中心矩是与图像的平移无关的。
当对边缘曲线进行尺度变化时，尺度的变化导致曲线长度的变化，相应的变化因子是k。此时尺度变化后的中心矩成为μ′pq=μpq×kp+q+1。
用零阶中心矩对其余各阶中心矩进行归一化，可以得到归一化的中心矩为
对曲线来说，要满足尺度不变性，从η′pq=ηpq可推出
γ=p+q+1 （4-22）
为了使矩描述子与平移、大小、旋转等因素无关，利用2阶和3阶归一化中心矩可以导出下面7个矩不变式：
由于φ25+φ27=φ3φ34，所以上面的7个矩不变式只有6个是独立的。
在不变矩的实际计算过程中，如医学图像，其不变矩数值分布范围非常大。而在识别过程中，如果不变矩特征值愈小，对识别结果的贡献就愈小；如果不变矩特征值愈大，对识别结果的贡献就愈大。为此，对7个不变矩进行如下修正，以调整其取值范围：
式中所进行的修正变换应综合考虑不变矩特征的大小及后续识别的结构特点。
有关图像目标的表示与识别的文章
- 详细阅读
-
彩色纹理图像特征提取方法研究详细阅读
由于本书第2章至第4章已经提出了三种灰度纹理图像的特征提取方法，并且HSV颜色空间中的亮度分量V就是灰度纹理图像，可将本书第2章至第4章提出的灰度纹理图像特征提取方法直接应用于HSV颜色空间中的V分量，从而实现灰度纹理特征的提取。......
2023-06-29
-
图像特征提取与选择的方法及应用详细阅读
图像特征的提取和选择是图像处理过程中很重要的环节，对后续图像分类有着重要的影响，并且具有样本少、维数高的特点。特征提取与特征选择就是最有效的降维方法，其目的是得到一个反映数据本质结构、识别率更高的特征子空间。上述特征提取方法是图像特征的初步获取，其各有利弊。针对不同的实际问题，可选择适当的图像特征提取方法。......
2023-11-08
-
区域生长法：基于图像特性的有效分割方法详细阅读
但是大多数区域分割都是非规则的形状，这时可以采用基于区域特性的图像分割方法，例如区域生长法、区域合并分裂法等。区域生长法也称为区域扩张法，其基本步骤可以如下描述。3）将获得的新区域当做新的种子区域继续进行2）的过程，直到没有满足条件的像素点时停止生长。4）区域生长停止的条件 即合适种子点停止生长。一般情况下，区域生长停止条件是结合生长准则来进行合理的设定。......
2023-11-24
-
基于图像处理的木材表面纹理特征提取方法详细阅读
所以，迄今为止关于木材表面纹理表达与分析的研究，基本上仍停留在定性描述为主，局部定量为辅的阶段。日本的仲村匡司采用计算机图形处理模拟制作了各种木材径切面纹理模型图片，并调查分析了“自然感”心理量与其他心理量以及纹理图形数字化参数之间的关系。其结果表明，“自然感”与“木纹相象感”和“喜好感”相关程度很高，可认为加强自然感是提高木纹仿制品视觉特性的有效途径之一。......
2023-11-19
-
Tennant法：一种有效的口腔健康护理方法详细阅读
Tennant法是目前世界上应用最广泛的方法，它是由美国学者Tennant和美国渔业野生动物协会于1976年共同开发。Tennant调查了美国21个州溪流的物理、生物和化学数据，Tennant用天然流量的多年平均流量的百分数作为基流标准。因此把年度分为各6个月的两段，10月至翌年3月为枯水季，4—9月为丰水季，对百分数比例有所调整。Tennant法还设置了河流暴涨状态，以体现洪水脉冲效应，维持栖息地质量。Tennant法计算基流的基准是自然水流。......
2023-06-27
-
口服避孕药：一种有效的避孕方法详细阅读
口服避孕药是甾体激素避孕方法中最主要的产品，是发达国家使用最广泛的避孕方法之一，约占已婚女性避孕措施的60%。复方长效口服避孕药：每月服1片可达到避孕1个月的目的，避免服药烦琐。目前，常用的有皮下埋植剂、阴道避孕环和宫内避孕系统。有性生活的育龄女性，身体健康，月经正常，自愿选择服药避孕者。服用避孕药应该严格遵循避孕药说明书。......
2023-12-03
-
基于计算机图像处理的木材纹理特征提取及分类方详细阅读
针对常见特征选择方法的不直接性，我们将子集评价函数直接选为分类器的识别率，提出一种基于模拟退火算法与最近邻分类器识别率的特征选择方法。因此，我们最终选用最近邻分类器识别率作为评价准则。模拟退火算法中最常用的是2变换法和3 变换法，这两种方法有着各自独特的优越性，我们将这两种方法随机交替使用获得了较好的效果。......
2023-11-19
相关推荐