基于竞争的分布式接入控制多址方式中，航天器用户通过接入控制协议实时获得信道接入信息，并通过相关算法进行竞争接入。在基于ALOHA竞争方式的多址协议中，数据包的碰撞概率会随着同时请求接入的卫星终端数量的增加而急剧增大，影响了系统的稳定性，极大限制了其在卫星通信系统中的应用。目前，改进型IEEE802.11无线局域网MAC协议接入控制方式主要支持短数据包业务传输，难以适用于大容量和实时性要求较高的业务。......
2023-07-02
基于梯度分布的描述子方案介绍
【摘要】：Lowe提出的SIFT描述子对后来的许多基于梯度分布的特征描述子都产生了深远的影响。圆形的高斯窗尽量减小那些远离特征区域中心的梯度值影响，这样就避免了微小变化引起的描述子突变。图4-6 由邻域梯度信息生成特征向量图4-6的右图所示的描述符是基于一个2×2个梯度方向直方图，Lowe建议在实际应用中采用16个直方图进行描述效果最好。基于梯度分布的特征描述子都可以较稳健的对发生几何形变、退化、受噪声干扰的图像局部特征进行准确的匹配。
Lowe提出的SIFT描述子对后来的许多基于梯度分布的特征描述子都产生了深远的影响。例如，GH和SC描述子的主要思想就和SIFT描述子类似，只是它们描述的是区域内边缘的分布，主要应用于边缘特征比较明显、稳定的图像；PCA-SIFT和GLOH描述子都是对SIFT描述子的扩展，它们在区域和梯度方向上采用了不同的描述精度，并用主分量分析对特征向量进行降维处理，进一步增强了描述子的鲁棒性和区分度。
为了使描述子具有旋转不变性，需要为每一个特征点指定一个方向，从而让局部特征描述子与这个方向因子相关。计算特征点邻域的梯度模值以及梯度方向的公式如下：
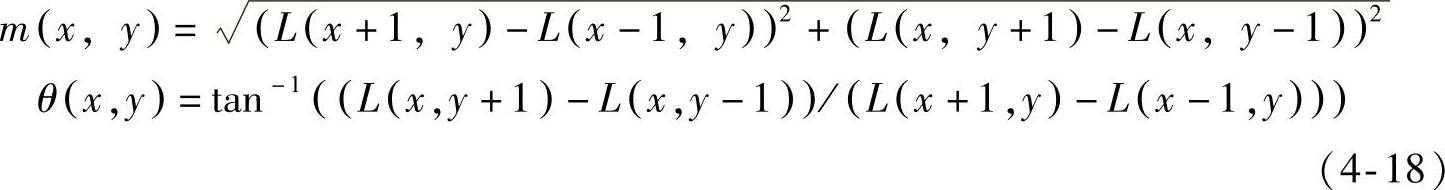
式中，L为每个特征点各自所在的尺度。在以特征点为中心的邻域窗口内计算像素的梯度方向直方图，直方图的范围是0°～360°，以10°为一个步长，共分为36个方向。如图4-5所示，在计算过程中需要一个的高斯权重窗（左图中的圆形），中心处的权值最大，边缘处的权值最小，右图给出了8个方向的直方图示例（实际应用中常采用36个方向）。
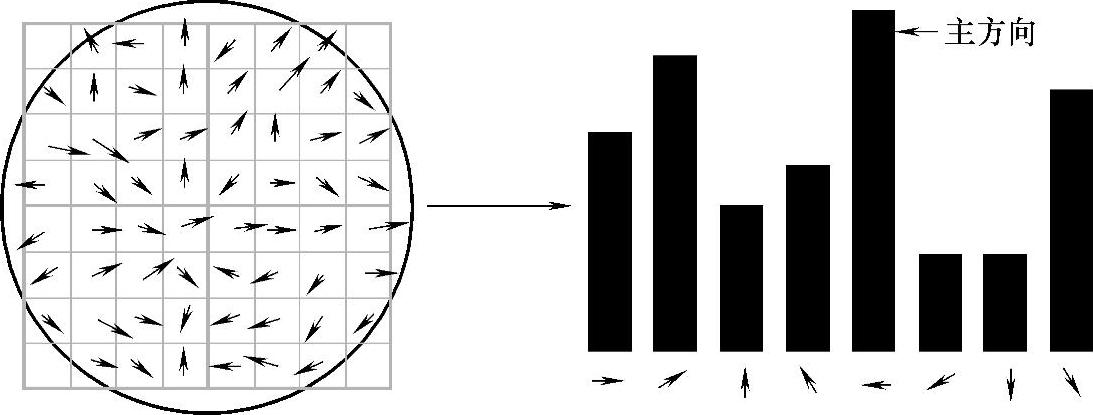
图4-5 由梯度方向直方图确定主梯度方向
为了增强匹配的稳定性，以梯度方向直方图的最大值作为该特征点的主方向，并选择大于主方向峰值80％的方向作为辅方向。虽然在相同位置和尺度可能创建多个特征点但方向不同，且15％的特征点被赋予多个方向，这明显提高了特征点的区分性。
如图4-6所示，每一个特征点都携带了三种信息——位置、尺度和方向，由此可以确定一个SIFT特征区域，可以将坐标轴旋转为特征点的方向，进而构造出独特性较高的特征描述子，且具有不受尺度、光照、视角变化影响的性质。左图中矩形的中心点表示当前特征点的位置，小箭头的长度代表梯度的幅值，箭头的方向表示梯度的方向。圆形的高斯窗（越靠近中心点，贡献越大）尽量减小那些远离特征区域中心的梯度值影响，这样就避免了微小变化引起的描述子突变。
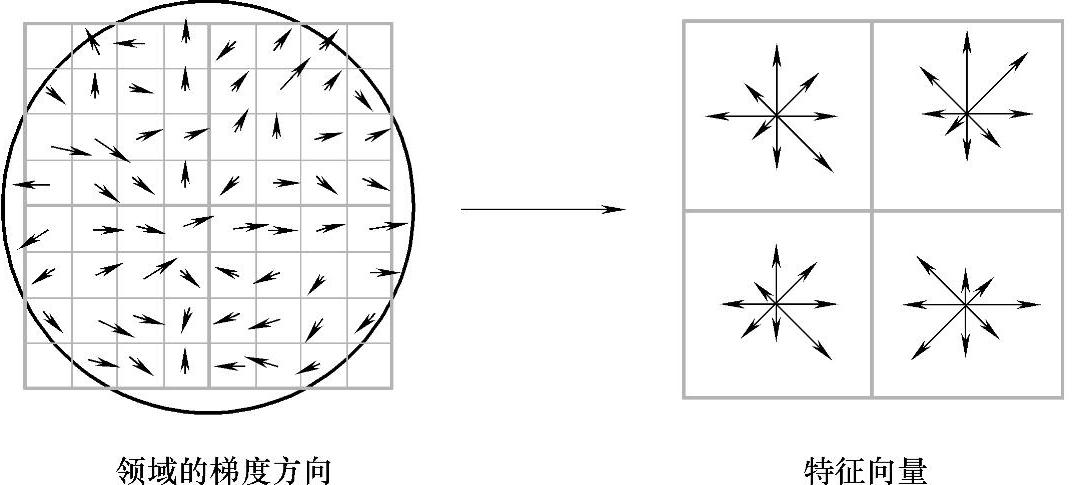
图4-6 由邻域梯度信息生成特征向量
图4-6的右图所示的描述符是基于一个2×2个梯度方向直方图，Lowe建议在实际应用中采用16个直方图进行描述效果最好。即以特征点为中心取16×16像素大小的邻域，将此邻域分为16个大小为4×4个像素的子区域，对每个子区域计算8方向的梯度方向直方图。根据子区域位置对相应的梯度方向直方图排序，就构成了一个4×4×8=128维的SIFT特征向量。如此一来，该特征描述子就消除了尺度变化、旋转变化等因素的影响，通过向量的长度归一化可以进一步消除光照变化的影响。
GLOH描述子是对SIFT描述思想的改进和发展，首先利用邻域像素的梯度方向分布为每个特征点指定方向参数，并将坐标轴旋转为该方向，以确保旋转不变性。然后在特征点所处的尺度空间（即高斯金字塔的某一层），取其周围的16像素16像素大小的邻域，用17层放射状同心圆来表示，并对每个子区域计算梯度方向直方图（梯度方向分为16种）。对17个子区域的16方向梯度直方图根据位置依次排序，这样就得到一个17×16=272维的向量。通过主分量分析（Principal Component Analysis，PCA）进行降维，最终得到一个128维的向量，在最大程度保留原始数据的同时大大减少了后续应用的计算时间。
基于梯度分布的特征描述子都可以较稳健的对发生几何形变、退化、受噪声干扰的图像局部特征进行准确的匹配。而且由于这些特征描述子在计算关键点方向时充分利用了邻域信息，这样在一定程度上可以避免在小运动物体上匹配特征点，因为小运动物体的邻域信息即使去除了尺度和旋转的因素后也仅是具备较少的梯度方向相似性；同时这些特征描述子在计算关键点处的梯度方向时都使用了直方图统计和高斯加权的思想，这就对存在定位偏差的特征点匹配提供了更好的适应性。
有关图像目标的表示与识别的文章
- 详细阅读
-
基于NNDR的匹配策略的介绍详细阅读
对SIFT特征的研究［146］表明，可以通过比较最近邻特征和次近邻特征的距离可以有效地甄别局部特征是否正确匹配。这就是最邻近距离比值法，其表述如下，如果待匹配特征为DA，其最邻近特征为DB，次邻近特征为DC，那么判断该特征匹配的条件为：该方法理论来源是，如果一个特征在一幅图像中与两个特征的距离都很相近，那么该特征的区分度较低，也违背了Marr提出的“匹配应该满足唯一性”的原则，会对图像相似度的判断产生干扰。......
2023-06-28
-
张量形状描述子在人体动作识别中的应用详细阅读
形状描述子三维轨迹的形状描述子是对各个离散轨迹点之间位置关系的一种表示。曲率表示运动轨迹曲线的局部形状变换，提取多尺度下曲率的过零点值，即空间极值点，将其作为形状描述子，这种方法称为曲率尺度空间。下面对3 种常用的形状特征描述子作简要介绍。该距离集合就是中心距函数形状描述子。根据上述分析，将利用欧氏距离描述运动轨迹形状的描述子，称为完整形状描述子。该完整形状描述子具有旋转、尺度和平移不变性。......
2023-10-28
-
基于模板匹配的检索方法的介绍详细阅读
这一模型意味着在我们的知识基础中，已经存储了数以百万计的不同模板——每一个可以辨识的不同物体或模式，都有一个与之匹配的模板存在。本书结合局部特征的特点和模板匹配的原理，提出了一种图像检索方法。如果局部特征和模板匹配的数量越多，则该幅图像和查询图相似的程度就越高。显然，模板匹配并不完全适合知觉原理的实际应用。......
2023-06-28
-
图像子带分解基于频带分割的编码技术详细阅读
基于分解子带的图像编码称为频带分割编码，其基本思想是把信号分解成低分辨率的平滑近似和高频细节两部分，分别称为低频子带和高频子带。对每个生成的子带又可以用同样的方式进一步分解。图7-25说明了一幅图像经过二级小波变换的过程以及形成的各个子带分布。为此，考虑设计基于ap2的图像分解和重构。实际上，对于二维图像的分解可通过一维滤波器分别在行列方向上进行。......
2023-06-23
-
有机氯农药含量分布的分析介绍详细阅读
DDT和HCH是历史上我国农业使用量最大的两种主要有机氯农药，也是本文着重研究和讨论的目标。漓江两个沉积柱中OCPs、HCHs和DDTs含量分布见图1。与这些沉积物柱芯样品相比，漓江沉积物柱芯样品有机氯农药污染程度高于珠江澳门河口和西藏羊卓雍湖，与太湖沉积物持平，低于洪湖沉积物柱芯。......
2023-06-26
-
家族企业治理结构的描述性分析：基于温州实证研详细阅读
表10企业资产规模3.2.2.5企业职工人数虽然我们调查的企业在资产具有一定规模，但是企业员工500人以上的企业占总数的仅43.8%，说明接受调查的温州民营企业还是以中等规模的企业为主。表12企业设立的时间续表3.2.2.7您家族企业所属的行业接受调查的温州企业主要集中于制造业，占据59.9%，其中鞋革20.4%，电器工业11.6%。这一行为说明温州的家族企业主不安于现状的框架，在现实中不按照常理出牌。......
2023-11-27
-
基于Agent交互协议的资源调度方案详细阅读
无论是哪种类型的资源受限项目调度问题，都需要将调度方案转化为有效的调度计划以便安排活动任务。调度计划是满足一系列优先级限制和资源限制的前提下制定的连续方法，主要有并行调度产生方案和串行调度产生方案两种。对于小规模和强资源限制的项目，并行调度计算结果优于串行调度，而大规模和适当资源限制的项目更适合串行调度方案。图3.5广义优先关系串行调度产生方案的目标流程初始化值及参数。......
2023-10-05
相关推荐