)∈l∞使得μ≤α 对任意的Banach 极限.若≤0,则≤α.......
2023-10-20
边缘点检测算子的应用的介绍
【摘要】：Canny的分析是针对一维边缘中的阶跃型边缘，Canny推导出的最优边缘检测器的形状与高斯函数的一阶导数类似，利用二维高斯函数的对称性和可分解性，可以很容易计算高斯函数在任意方向上的方向导数与图像的卷积。因此，在实际运用中可以选取高斯函数的一阶导数作为阶跃边缘的次最优检验算子。以上为Canny二维最优阶跃边缘检测算子的数学推导。
基于形状的检测算子一般都是将边缘点作为特征点，从而进行特征描述的。Canny［155］提出了评价边缘检测算法性能优良的三个指标：
1）高的信噪比；
2）精确的定位性能；
3）对单一边缘响应是唯一的。
Canny算子首次将上述判据用数学的形式表达出来，然后采用最优化数值方法，得到对应给定边缘模型的最佳边缘检测模板。对于二维图像，需要使用若干方向的模板分别对图像进行卷积处理，再取最可能的边缘方向。Canny的分析是针对一维边缘中的阶跃型边缘，Canny推导出的最优边缘检测器的形状与高斯函数的一阶导数类似，利用二维高斯函数的对称性和可分解性，可以很容易计算高斯函数在任意方向上的方向导数与图像的卷积。因此，在实际运用中可以选取高斯函数的一阶导数作为阶跃边缘的次最优检验算子。
设图像f (x，y)，二维高斯函数如式（2-2）所示，由卷积求导性质可知，G∗f (x，y)的梯度为
∇[G∗f (x，y)]=∇G∗f (x，y) （4-14）梯度的模值，即G∗f (x，y)的最大方向导数为
以其作为边界强度。
梯度的单位方向矢量
式中
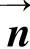或α给出了边界的法线方向。
以上为Canny二维最优阶跃边缘检测算子的数学推导。在实际应用中，可以将原始模板截断到有限尺寸N，为了提高运算速度，可以将∇G的二维卷积模板分解为两个一维卷积模板。
根据Canny边缘的提取原则。当一个像素满足以下三个条件时，则被认为是图像的边缘点：
1）该点的边缘强度大于沿该点梯度方向（这里指正反向）上的两个相邻像素点的边缘强度——主要作用是准确定位并控制边缘宽度为一个像素点。
2）与该点梯度方向上相邻两点的梯度方向之差小于45°——给出光滑性约束，克服随机因素的影响。
3）以该点为中心的3×3邻域中的边缘强度极大值小于某个阈值——保持边缘强度相对一致，去除噪声产生的伪边缘。
有关图像目标的表示与识别的文章
- 详细阅读
-
视觉测量技术中的边缘点检测及多尺度算法详细阅读
空域微分算子法这也是传统的边缘检测算法。小波多尺度检测利用多种尺度的边缘检测算子对图像进行检测，然后综合它们的检测结果以获得理想的输出。基于数学形态学的边缘检测数学形态学是一种有代表性的非结构数学方法。其中，空域微分算子法、曲面拟合法等属于经典的边缘检测算法。图像处理中基于一阶微分的边缘检测是通过梯度法实现的。图4.12所示模板表示图像3×3区域的图像点。......
2023-11-24
-
非线性算子的性质及应用详细阅读
非线性算子的性质包括连续性、有界性、全连续性、可微性等.这是一些基本概念和性质,在后面各章中都要用到.设E1和E2时两个实Banach 空间,D E1.设A∶D→E2为非线性的.定义1设x0∈D.若ε>0,δ=δ(x0,ε)>0 使得当x ∈D且‖x-x0‖ < δ 时,恒有‖Ax -Ax0‖ < ε,则称A 在x0连续;若A 在D 中每一点都连续,则称A 在D 上连续;若上述δ 只与ε 有关而......
2023-10-20
-
生产调度中的遗传算子应用详细阅读
分别是拒绝策略、 修复策略、 改变遗传算子策略和惩罚策略。本书采用改变遗传算子的策略， 用分组交叉的算子来实现个体的交叉， 这样， 不仅易于实现， 而且不会产生非法染色体。如图6-1 所示：图6-1交叉算子遗传算法是群体进化的一种方法， 其最大优势在于同时使用多个点的搜索信息， 在各种方案之间进行选择、 交叉、 变异等运算。图6-2遗传算法实施流程图......
2023-06-20
-
单体轴测投影图的绘制的介绍详细阅读
图6-3圆柱正等轴测投影图的绘制（续）画出轮廓线；检查加深；圆柱正等轴测投影最后成图图D.3 流水线操作阶段如果我们假设每个流水线操作阶段有10ns的延迟，然后如果每条指令要求在下一条指令获得前执行完成，那么每条指令就花40ns。这种情况下，处理器一次执行4条指令。只有当流水线操作接到一个稳定的指令流，并不受限制地使用所需操作数作为指令的输入输出，才能达到这样的性能。......
2023-06-23
-
堆焊的特点及应用介绍详细阅读
等离子弧堆焊有冷丝等离子堆焊、热丝等离子堆焊、预制型等离子弧堆焊和粉末等离子弧堆焊。其中粉末等离子堆焊粉末具有制作简单、熔敷率高、粉末利用率高等优点，应用广泛。电渣堆焊的熔敷高，气体含量少，质量好，但易过热。D307与高速钢W18Cr4V成分相近，具有良好的热硬性，在600℃以下可保持高硬度，既可用于冷作模具堆焊，也可用于热作模具堆焊。......
2023-06-26
-
UGNX9.0超级学习手册：曲面边缘的边缘处详细阅读
图4.6.29 从片体中移除修剪图4.6.30 从片体中移除修剪方式三：替换边替换边就是用片体内或片体外的新边来替换原来的边缘。下面以图4.6.35为例来说明更改片体边缘的一般操作过程。在图形区选取图4.6.36所示的曲面边缘，系统弹出图4.6.37所示的“更改边”对话框（三）。图4.6.38所示“更改边”对话框（四）中的各按钮说明如下：●：用于将曲面的边缘与选定的曲线匹配。......
2023-11-20
-
测量技术了解与应用的介绍详细阅读
从最高一级标准到实际应用的测量仪器所进行的量值传递是各个国家各级计量部门的主要职能。联立测量又称为组合测量，它是一种兼用直接测量和间接测量的方法。为了监视生产过程，或在生产线上监测被加工工件质量的测量称为在线测量；反之，称为离线测量。例如，体检中的身高、体重测量，温度计测气温等。精密测量时一般采用数字式测量方法。以仪表指针的偏移量表示被测量的测量方式称为偏差式测量。......
2023-06-22
相关推荐