Canny的分析是针对一维边缘中的阶跃型边缘，Canny推导出的最优边缘检测器的形状与高斯函数的一阶导数类似，利用二维高斯函数的对称性和可分解性，可以很容易计算高斯函数在任意方向上的方向导数与图像的卷积。因此，在实际运用中可以选取高斯函数的一阶导数作为阶跃边缘的次最优检验算子。以上为Canny二维最优阶跃边缘检测算子的数学推导。......
2023-06-28
高斯差分检测算子简介
【摘要】：高斯差分算子是在多尺度空间中寻找稳定有效的特征区域。图4-1 高斯拉普拉斯函数与高斯差分函数图4-2 高斯金字塔和高斯差分金字塔的构造示意图限于篇幅，图4-2只给出了第一层和第二层高斯差分图像的计算。如图4-2中右图的五角星符号所标识，由于需要与相邻尺度的点进行比较，所以在每层高斯差分金字塔的一组图像中只能检测到两个尺度的极值点。
近几年，高斯差分（Difference of Gaussian，DoG）、SalReg（Salient Re-gions）、MSER（Maximally Stable Extremal Regions）算法的相继出现，代表着基于外观的检测算子开始广泛应用于机器视觉领域。高斯差分算子是在多尺度空间中寻找稳定有效的特征区域。Koendetink和Lindeberg等人［150-152］证明了高斯卷积核是实现尺度变换的唯一线性核，所以，一幅二维图像I (x，y)的尺度空间定义为
L (x，y，σ)=G (x，y，σ)∗I (x，y) （4-1）
式中，符号∗表示卷积，(x，y)代表图像中像素的位置，而尺度可变高斯函数为
利用不同尺度的高斯差分算子与图像进行卷积运算，可以求取尺度空间极值，计算公式如下：
D (x，y，σ)=[G (x，y，kσ)-G (x，y，σ)]∗I (x，y)
=L (x，y，kσ)-L (x，y，σ) （4-3）
其中，L代表了图像的尺度空间，k是常数，一般取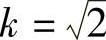
。这里选择高斯差分函数的原因主要有两个：一是其计算效率较高；二是它可以作为尺度归一化的高斯拉普拉斯函数（Laplacian of Gaussian，LoG）——σ2▽2G的一种近似［152］，如图4-1所示。
通过与其他特征提取算子（如Harris、Hessian算子）的实验比较，Mikola-jczyk等人［154］发现基于σ2∇2G的极大值和极小值能够产生更为稳定的局部特征。D (x，y，σ)与σ2∇2G的关系可以从如下公式推导得到：
利用差分近似替代微分，则有
因此，有
G (x，y，kσ)-G (x，y，σ)≈(k-1)σ2∇2G （4-6）
其中k-1是个常数，并不影响极值点位置的求取。
如图4-2所示，Lowe等人［153］提出了一种构造D（x，y，σ）的有效方法。左侧是不同尺度空间中的图像金字塔，右侧显示了将每层金字塔中相邻图像相减所生成的高斯差分图像的结果。
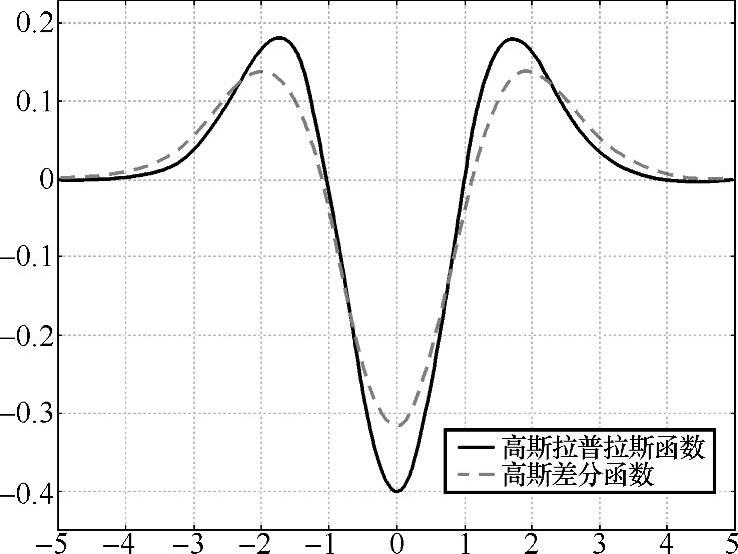
图4-1 高斯拉普拉斯函数与高斯差分函数
图4-2 高斯金字塔和高斯差分金字塔的构造示意图
限于篇幅，图4-2只给出了第一层和第二层高斯差分图像的计算。在实际应用中，高斯金字塔一般选择4层，每层有5幅一组的尺度图像。在目前常用的设计方案中，第一层的第一幅图像是放大2倍的原始图像，其目的是为了得到更多的特征点。
图4-3是利用一幅关于爱因斯坦的图像构造高斯金字塔和高斯差分金字塔的示例。图4-3b所示的高斯差分图像是通过图4-3a金字塔中对应层上的相邻图像相减而得到的。
图4-3 两种图像金字塔的示例
a）高斯金字塔 b）高斯差分金字塔
图4-4所示为如何从高斯差分金字塔的分层结构中提取出图像的极值点作为候选的特征点，就是将每个检测点与其相邻点（图像域和尺度域）进行逐个比较，得到的局部极值位置即为该特征点所处的位置和对应的尺度。如图4-2中右图的五角星符号所标识，由于需要与相邻尺度的点进行比较，所以在每层高斯差分金字塔的一组图像中只能检测到两个尺度的极值点。
由于DoG算子对噪声和边缘较为敏感，因此，在上面DoG尺度空间中检测到的局部极值点还需要经过进一步的检验才能精确定位为特征点。通过拟合三维二次函数可以较精确地计算特征点的位置和尺度，同时还可以去除对比度较低的特征点以及稳定性较差的边缘响应点［146］。
获取特征点处的拟合函数为
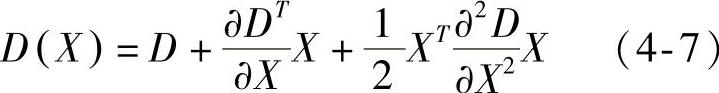
求导并让方程等于零，可以得到极值点：
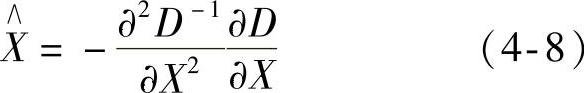
对应极值点，方程的值为
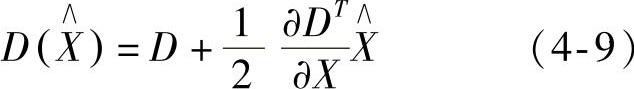
如果D (X∧)≤0.03，则视为对比度较低的候选特征点，并予以剔除。
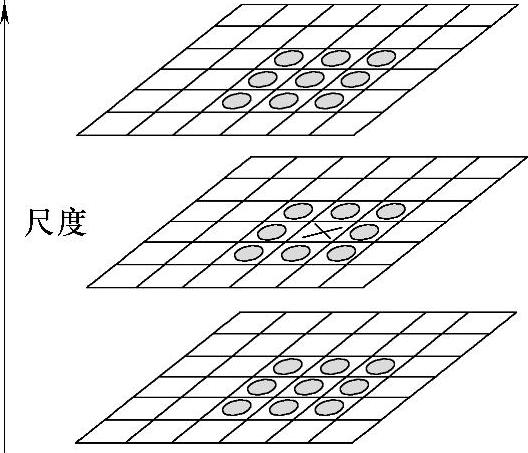
图4-4 尺度空间的极值检测
（来源：Lowe，2004）
因为DoG算子会产生较强的边缘响应，所以需要对这些不稳定的点进行检测。首先获取该点处的Hessian矩阵：
H的特征值α和β代表x和y方向的梯度：
Tr (H)和Det (H)分别表示矩阵H的迹与行列式。假设α是最大的特征值，β是较小的特征值，令α=rβ，则
式（4-12）的值越大也就是两个特征值之比越大，这就说明在某一个方向上的梯度值越大，同时另一个方向上的梯度值越小，这种情况恰恰符合边缘响应的条件。一般取r=10，并检测是否符合以下条件，就可以剔除边缘响应点：
有关图像目标的表示与识别的文章
- 详细阅读
-
差异表达基因检测方法简介详细阅读
许多研究者对此进行了研究，并提出了多种差异表达基因检测方法。OPA方法采用基因组数据异常分析的非参数方法对某特定基因进行检测，这个基因的基因芯片数据的一个组中只有一部分样本相对于另一组样本过高表达，剩余的样本没有差异表达的迹象。PACK方法、PADGE方法、PPRM方法、OPA方法、LRS方法也研究了假定癌症组子集样本相对于正常组样本有过高或过低表达的差异基因表达检测统计方法。......
2023-11-21
-
茶氨酸检测方法简介详细阅读
茶氨酸是一种天然的氨基酸，存在于茶叶中。茶氨酸是多极化合物，等电点5.83，也就是p H＞5.8整个分子显负性，p H＜5.8整个分子就显正性。为了延长保留时间、提高分离效果，本方法使用癸烷基磺酸钠作离子对加在移动相里，p H 调节至2.0。②样品液的配制：称取一定量碾碎的含有约20 mg茶氨酸的样品，转入50 mL容量瓶中，加入30 m L水，振荡2 min，超声15 min，再加水至刻度，摇匀后离心5 min，吸取上层清液即可注射。......
2023-07-02
-
食品安全检测技术简介详细阅读
食品安全检测技术呈现出一些新的发展趋势，日益趋向于高技术化、系列化、速测化、便携化。这些新型生物检验技术在食品安全检测中的应用必将成为未来食品行业发展的趋势，为该行业的发展带来新的光芒。⑨利用现代生物技术检测方法可以快速、准确地测定食品中的有害有毒物质，更好地保障食品的安全食用。......
2023-11-18
-
高等数学（上、下册）：差分方程简介及一阶、二详细阅读
一、差分与差分方程的一般概念定义6.3 设函数y=f，记为yx，则差yx+1-yx称为yx的一阶差分，简称为差分，记为Δyx，即Δyx=yx+1-yx.定义6.4 yx的一阶差分的差分Δ（Δyx）=Δ=-，记为Δ2yx，称为yx的二阶差分，即Δ2yx=Δ（Δyx）=yx+2-2yx+1+yx.同样定义三阶差分，四阶差分，…......
2023-11-22
-
显示部件的检测和代换方法简介详细阅读
显示部件若出现故障，则会造成屏幕无法正常显示图像，这时就需要对显示部件里面的元件或电路进行检测与代换。图5-20 12864图形点阵模块的实物外形对于液晶显示模块的检测，可以分别通过检测其引脚的供电电压、关键脚的数据信号波形及背光灯电压来确定。图解演示12864图形点阵型LCD显示模块背光灯正向阻值的检测方法如图5-24所示。图5-24 检测LED背光灯的正向阻值正常情况下，其正向阻值应为无穷大。......
2023-06-26
-
全球定位系统简介及RTK实时动态差分法详细阅读
GPS系统主要由空间星座、地面监控、用户设备三大部分组成。图252RTK原理2.RTK定义及原理实时动态差分法Real-time kinematic是以载波相位观测量为根据的实时差分GPS测量，它能够实时地提供测站点在指定坐标系中的厘米级精度的三维定位结果。RTK测量系统通常由三部分组成，即GPS信号接收部分、实时数据传输部分和实时数据处理部分。......
2023-06-29
- 详细阅读
相关推荐