由线性判别函数的设计过程可知,对于线性可分集,总能找到使模式样本正确划分的解。d维空间中线性判别函数的一般形式为g=ωX+b,分类面方程为:ωX+b=0将判别函数进行归一化,使两类所有样本都满足|g|>1,这样分类间隔就等于2/‖ω‖。对于线性不可分问题,可以用类似于广义线性判别函数的方法,通过事先选择好的非线性映射将输入模式向量映射到一个高维空间,在这个空间中构造最优分界超平面。......
2023-06-16
支持向量机是Vapnik及其合作者[130]根据结构风险最小化原则提出的一种在高维特征空间使用线性函数假设空间的学习系统。支持向量机是机器学习领域若干标准技术的集大成者。它集成了最大间隔超平面、Mercer核、凸二次规划、稀疏解和松弛变量等多项技术。在若干挑战性的应用中,获得了目前为止最好的性能。
1.线性分类
两类模式(正类和负类)的识别通常用一个实数函数f:X⊆Rn→R(n为输入维数,R为实数)。通过执行如下操作:当f(x)≥0时,将输入x=(x1,x2,…,xn)′标记为正类,否则,将其标记为负类。当f(x)(x∈X)是线性函数时,f(x)可以写成如下形式:
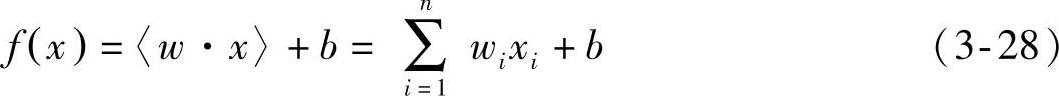
式中,(w,b)∈Rn×R,是控制函数的参数,决策规则由函数sgn(f(x))给出,通常sgn(0)=1,学习意味着要从数据中获得这些参数;“·”是向量点积。
该类方法的几何解释是,方程式〈w·x〉+b=0定义的超平面将输入空间X分成两个部分。如图3-4所示,黑斜线表示超平面,w是超平面的法线方向。当b值变化时,超平面平行于自身移动。因此,如果表达Rn中所有可能的超平面,一般要包括n+1个可调参数的表达式。
如果训练数据可以无误差地被划分,那么,以最大间隔分开数据的超平面称为最优超平面,如图3-5所示。
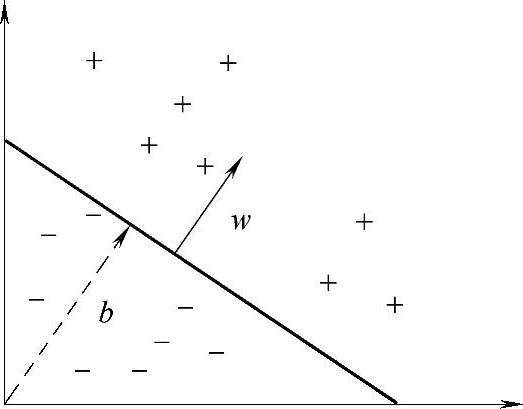
图3-4 二维训练集的分开超平面(w,b)
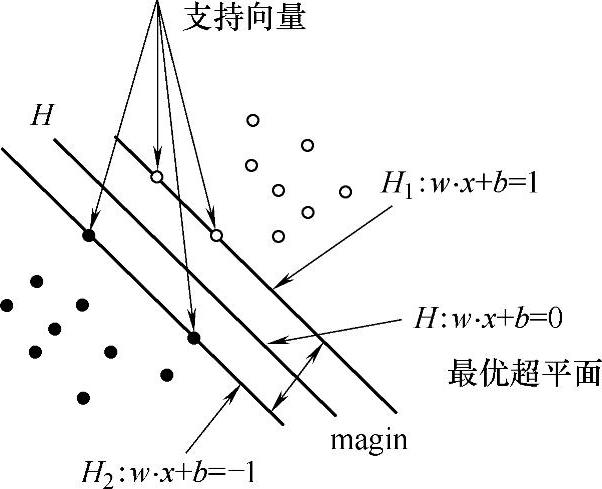
图3-5 最优超平面
对于多个模式类的分类问题,输出域是Y={1,2,…,m}。线性学习器推广到m(m∈N,m≥2)类是很直接的:给每个类关联一个超平面,然后,将待分类的数据点赋予超平面离其最远的那一个类。输入空间分为m个简单相连的凸区域。
2.线性不可分
对于非线性问题,可以把样本x映射到某个高维特征空间,在高维特征空间中使用线性学习器。因此,考虑的假设集是这种类型的函数:

式中,ϕ:X→F是从输入空间到某个特征空间的映射,如图3-6所示。也就是说,建立非线性分类器需要分两步:首先使用一个非线性映射函数将数据变换到一个特征空间F,然后在这个特征空间上使用线性分类器。
线性分类器的一个重要性质是可以表示成对偶形式,这意味着假设可以表达为训练点的线性组合,因此,决策规则(分类函数)可以用测试点和训练点的内积表示:
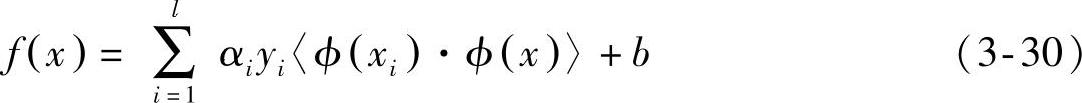
式中,l是样本数目;αi是个正值导数,可通过学习获得;yi为类别标记。如果有一种方法可以在特征空间中直接计算内积〈ϕ(xi)·ϕ(x)〉,就像在原始输入点的函数中一样,那么,就有可能将两个步骤融合到一起建立一个非线性分类器。这样,在高维空间内实际上只需要进行内积运算,而这种内积运算是可以利用原空间中的函数实现的,我们甚至没有必要知道变换的形式。这种直接计算的方法称为核(Kernel)函数方法。
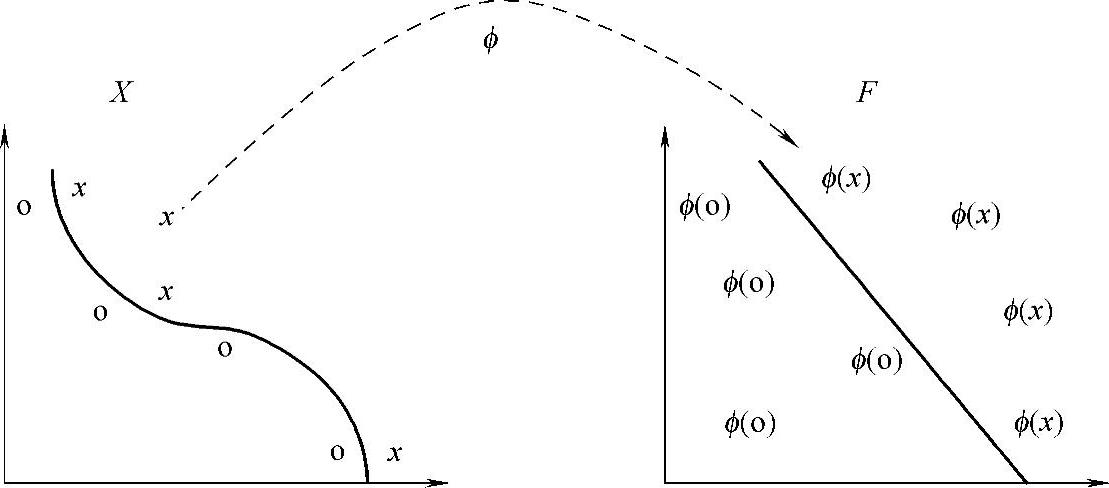
图3-6 简化分类任务的特征映射
3.构造核函数定义3-1核是一个函数K,对于所有x,z∈X,满足
K(x,z)=〈ϕ(x)·ϕ(z)〉 (3-31)
这里ϕ是从X到特征(内积)空间F的映射。
一旦有了核函数,决策规则就可以通过对核函数的l次计算得到
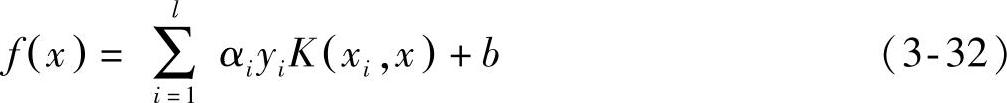
那么,这种方法的关键就是如何找到一个可以高效计算的核函数。
核函数要适合某个特征空间必须是对称的,即
K(x,z)=〈ϕ(x)·ϕ(z)〉=〈ϕ(z)·ϕ(x)〉=K(z,x) (3-33)
并且,满足下面的不等式:
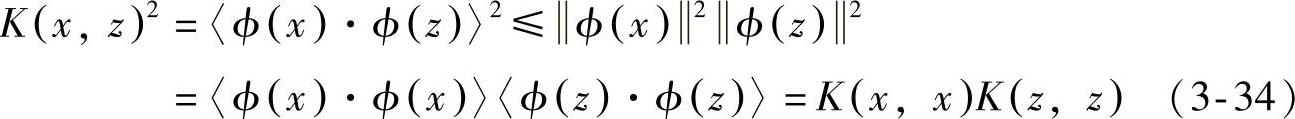
其中, 是欧氏模函数。但是,这些条件对于保证特征空间的存在时不充分的,还必须满足Mercer定理的条件,对X的任意有限子集,相应的矩阵式半正定的。也就是说,令X是有限输入空间,K(x,z)是X上的对称函数。那么,K(x,z)是核函数的充分必要条件是矩阵
是欧氏模函数。但是,这些条件对于保证特征空间的存在时不充分的,还必须满足Mercer定理的条件,对X的任意有限子集,相应的矩阵式半正定的。也就是说,令X是有限输入空间,K(x,z)是X上的对称函数。那么,K(x,z)是核函数的充分必要条件是矩阵
K=(K(xi,xj))ni,j=1 (3-35)是半正定的(即特征值非负)。
根据泛函的有关理论,只要一种核函数满足Mercer条件,它就对应某一空间中的内积。目前SVM常用的核函数有
线性核:K(x,z)=〈x·z〉 (3-36)
多项式核:K(x,z)=(〈x·z〉+c)d,其中c≥0,d∈N;当c=0时,称为齐次多项式核,当c>0时,称为非齐次多项式核。 (3-37)
高斯(径向基)核: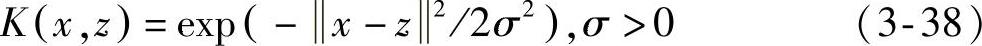
Sigmoid核: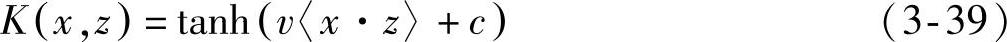
有关图像目标的表示与识别的文章

由线性判别函数的设计过程可知,对于线性可分集,总能找到使模式样本正确划分的解。d维空间中线性判别函数的一般形式为g=ωX+b,分类面方程为:ωX+b=0将判别函数进行归一化,使两类所有样本都满足|g|>1,这样分类间隔就等于2/‖ω‖。对于线性不可分问题,可以用类似于广义线性判别函数的方法,通过事先选择好的非线性映射将输入模式向量映射到一个高维空间,在这个空间中构造最优分界超平面。......
2023-06-16

支持向量机是机器学习中的一项新技术,是借助于最优化方法来解决机器学习问题的新工具,开始成为克服维数灾难和过学习等困难的强有力的手段。支持向量机方法建立在统计学理论的VC维理论和结构风险最小原理基础之上,根据有限样本在模型的复杂性和学习能力之间寻求最佳折中,以期获得最好的推广能力。支持向量机正是这样一种努力最小化结构风险的算法。这个归一化的结果便是支持向量机的几何间隔。......
2023-06-28

6.3.3 向量的表示法6.3.4 向量大小的计算6.3.5 向量的平行、相等与相反的定义向量具有大小与方向的双重属性,因而在此描述与说明向量平行、相等与相反。......
2023-06-29

支持向量机是由Vapnik[7]提出的一种机器学习方法,主要有支持向量分类和支持向量回归两种算法。由于SVR是目前结构可靠度分析中的一种较为新颖的方法,下文将简单介绍SVR在结构响应函数拟合应用中的相关理论。SVR学习理论主要是通过如式(3.2)所示的ε敏感函数[8]来控制SVR模型的拟合误差。由式(3.5)可得到SVR模型的函数表达式:为了提高建立SVR模型的效率与精度,可通过对输入样本点及SVR模型参数进行优化。......
2023-09-19

1.液压凿岩机的分类液压凿岩机是近几年来出现的一种新型凿岩机,基本可以分为两种类型:一种是小型手持式,其冲击能量较小,主要是用来代替传统的风镐,大多数与小型挖掘装载机、液压工程车等配套使用;另一种是大型机载式,这类液压凿岩机大多是以液压挖掘机的反铲作业装置为基础,将反铲斗换装成凿岩机的工作,由挖掘机驾驶员在驾驶室内进行操作。......
2023-06-29

朴素贝叶斯分类器进行目标分类的基本思想是利用特征项和类别的联合概率来估计给定目标的类别概率。理论上,朴素贝叶斯分类器与其他分类方法相比具有最小的误差率。但是该模型在分类识别中假设特征项之间相互独立,而这个假设在实际应用中往往是不成立的,这给朴素贝叶斯分类器的正确分类带来了一定影响。因此,近年来大量的研究工作致力于改进朴素贝叶斯分类器,主要集中在选择特征子集和放松独立性假设在两个方面。......
2023-06-28

一个目标在上述约定下可以看成是n维空间中的一个向量,这就是向量空间模型的由来。下面结合目标的表示,给出其定义。,td};2)依据目标特征项序列,对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理,将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2023-06-28
相关推荐