柴油燃油压缩为很高的压力,这会影响燃油喷射量,因此这在喷射调节系统中成为应考虑的重要因素。另外,燃油喷射量的改变会带来废气排放量和输出功率的变化。在传统的直列式和分配式燃油喷射系统中,喷射时间以输送时间为依据决定。......
2023-06-28
火箭喷管是把燃烧室中产生的高温、高压排气向外喷出,通过其反作用力获得推力的装置。在本节,对于以等熵过程流过喷管的排气流量、速度,以及压力比对这些参数的影响进行分析。实际火箭喷管内排气流动是排气和喷管壁面之间产生摩擦,发生通过喷管壁面的热传递(热损失),根据情况会发生冲击波,因此不是等熵过程。
为了说明理想火箭喷管内的流动,假设如下理想状态:
②燃烧室和喷管内部的排气流动为正常状态。
③燃烧室内的气体状态为滞止状态,压力和温度保持不变。
④喷管内工质气体的流动是一维正常流动,即工质气体的性质和速度仅在喷管的轴向不同,垂直与轴的方向上保持不变。
⑤喷管壁面没有摩擦和热传递,喷管内气体为等熵流动。
1.喷管出口速度
现在对推力室的收敛-扩散喷管内排气流动进行分析。因喷管入口为燃烧室,喷管入口状态参数以总参数表示。把正常状态能量守恒以总焓h0表示为
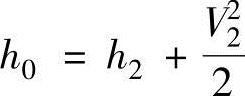
如果把焓以h=cpT表示,喷管出口速度V2可以表示为
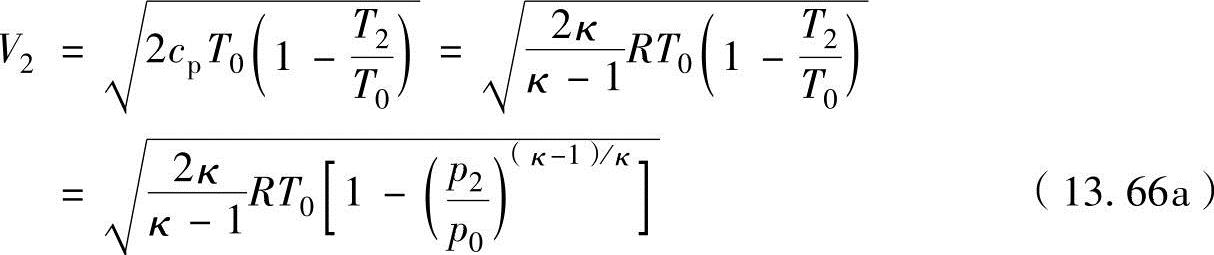
式(13.66a)可以用如下的无量纲喷管出口速度表示为

式中,质量定压热容引用了cp=κR/(κ-1),温度比T2/T0引用了等熵过程的理想气体状态方程“Tp(1-κ)/κ=C”。可以看出,喷管出口速度V2在燃烧室状态(p0,T0,v0)一定时,是质量热容比κ和压力比p2/p0(或出口压力p2)的函数。喷管出口速度随压力比的减小而增大,最大速度V2,max为在出口压力p2=0时,即燃烧气体向真空膨胀时出现,其计算式为

最大排气速度V2,max称为等熵速度,表示燃烧气体的热能全部转换为轴向速度。
图13-23所示为通过式(13.66b)的无量纲喷管出口速度对逆压力比p0/p2和质量热容比κ的关系曲线。可以看出,出口速度随逆压力比的增大而增加,但其增加率较小,并且随质量热容比的减小而增加。

图13-23 无量纲排气速度
2.喷管通过流量
在喷管内流过各端面的流量,质量守恒式“ 一定”成立。如果引用理想气体等熵过程的状态方程ρp01/κ=ρ0p1/κ、理想气体的状态方程ρ0=p0/(RT0)和任意端面上的速度V式(13.66),喷管内流过任意端面上的质量流量率
一定”成立。如果引用理想气体等熵过程的状态方程ρp01/κ=ρ0p1/κ、理想气体的状态方程ρ0=p0/(RT0)和任意端面上的速度V式(13.66),喷管内流过任意端面上的质量流量率 可以表示为
可以表示为
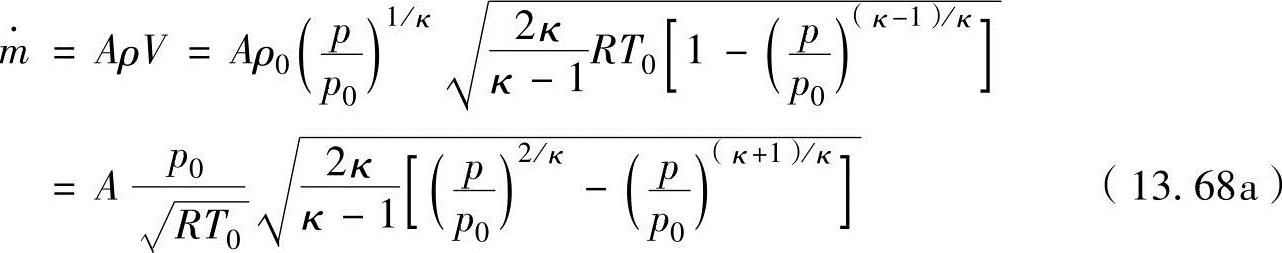
式(13.68a)可以用无量纲流量变量表示为

从上式中可知,当喷管入口(燃烧室)的状态(p0、T0等)和喷管内的端面积A不变时,流过喷管的质量流量率 与压力比p/p0有关。图13-24所示为无量纲流量变量与压力比p/p0和质量热容比κ的关系曲线。如图所示,当压力比为p/p0=1时,因没有压力差,质量流量率为0,在p/p0=0时也为0,由此可以知道存在无量纲流量变量达到最大的压力比,即临界压力比。这表示在临界压力比状态流过喷管的流量会达到最大。
与压力比p/p0有关。图13-24所示为无量纲流量变量与压力比p/p0和质量热容比κ的关系曲线。如图所示,当压力比为p/p0=1时,因没有压力差,质量流量率为0,在p/p0=0时也为0,由此可以知道存在无量纲流量变量达到最大的压力比,即临界压力比。这表示在临界压力比状态流过喷管的流量会达到最大。

图13-24 压力比与无量纲流量之间的关系
流过喷管的质量流量率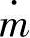 可以用喷管喉的状态参数表示。这是在式(13.68)中用喷管喉的端面积A和压力p代替面积At和压力pt即可。可以表示为
可以用喷管喉的状态参数表示。这是在式(13.68)中用喷管喉的端面积A和压力p代替面积At和压力pt即可。可以表示为

或
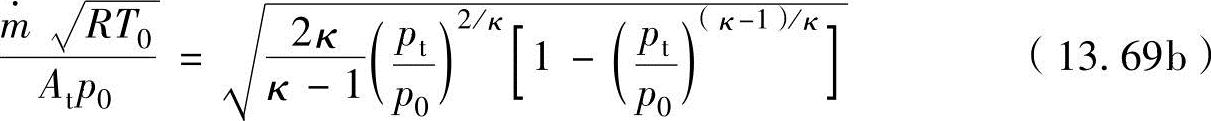
3.背压对流过喷管流量的影响
喷管出口速度、流动流量会受到背压(外界压力)的影响。在喷管出口端面上,排气压力pe与背压pa如果相同,推力系数会达到最大,燃烧气体会膨胀到最佳状态,但是如果不同,会发生膨胀不足或膨胀过度现象。观察背压pa对流过喷管的质量流量率的影响,就可以容易理解上述观点。
(1)收敛喷管 现在对流过收敛喷管的亚音速流动进行分析。对于在入口条件(燃烧室的总参数p0,T0等)一定,将背压pa从燃烧室压力p0开始逐渐降压时,对流过喷管的质量流量率m·与喷管出口端面上的排气压力pe的变化进行分析,如图13-25a所示。由此可以知道如下事实:
①pa=p0:如果背压与入口压力相同,喷管内没有排气的流动,如图13-25a所示,在喷管内的压力分布均匀。
②p0>pa>p*:背压pa大于临界压力p*和小于入口压力p0时,排气流过喷管时压力下降,在喷管出口排气压力pe与背压相等。
③pa≤p*:背压pa小于或等于临界压力p*时,喷管出口压力pe降低到临界压力p*。这表示即使背压小于临界压力,只要喷管内的压力分布与临界压力时相同,也不能进一步发生变化。
图13-25b上图所示为随压力比pa/p0变化的流过喷管的质量流量率m·。质量流量率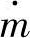 随压力比pa/p0的减小而增加,压力为pa=p*时达到最大值。压力比即使下降到临界压力比p*/p0以下,
随压力比pa/p0的减小而增加,压力为pa=p*时达到最大值。压力比即使下降到临界压力比p*/p0以下, 也保持不变。因此,流过喷管的质量流量率在临界压力比时达到最大,此时的流动称为被风阻(窒息)。图13-25b下图所示背压pa对出口压力pe的影响。从图中可以看出下列关系。
也保持不变。因此,流过喷管的质量流量率在临界压力比时达到最大,此时的流动称为被风阻(窒息)。图13-25b下图所示背压pa对出口压力pe的影响。从图中可以看出下列关系。
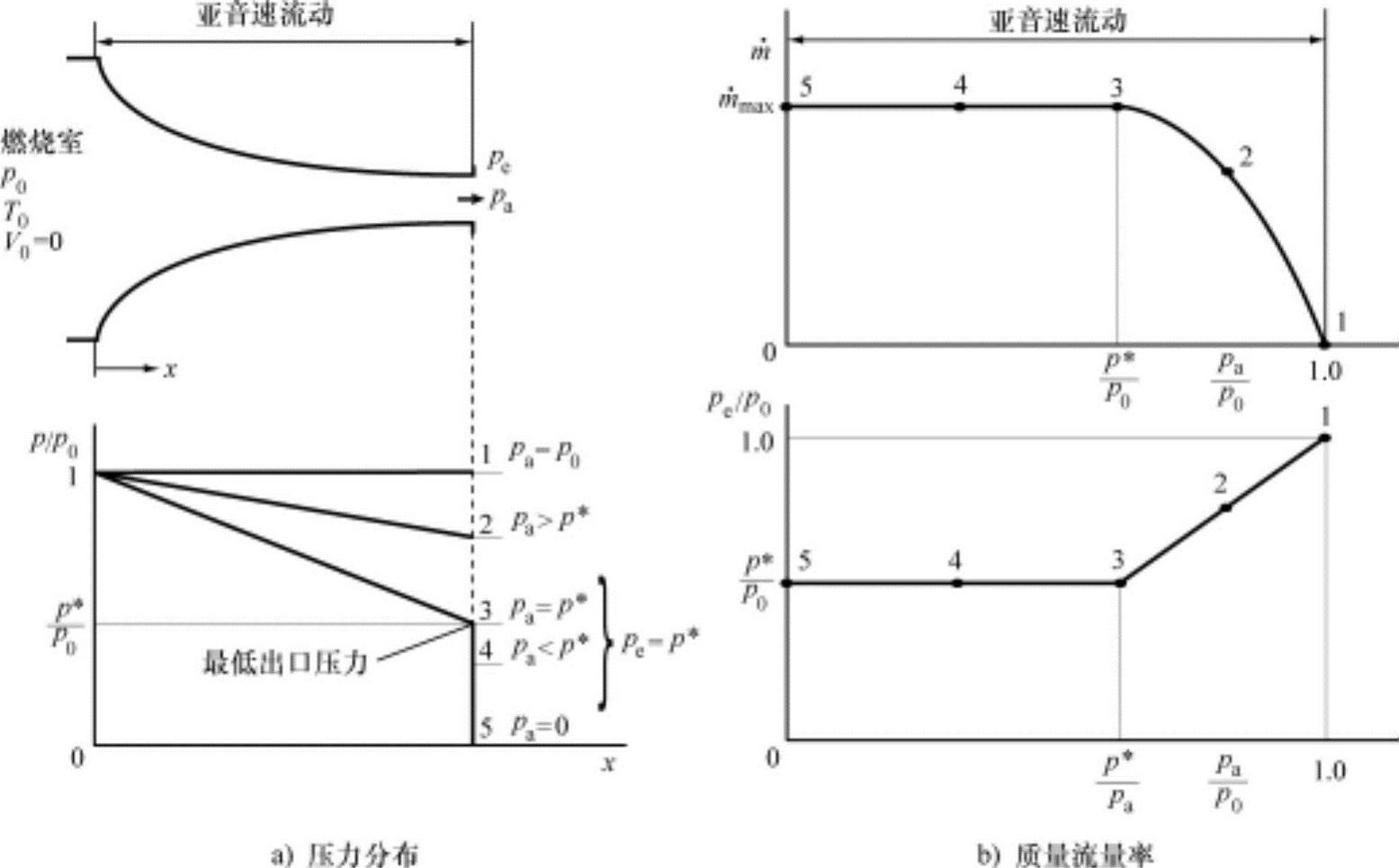
图13-25 收敛喷管内的压力分布

这表示即使背压为临界压力以下,只要在收敛喷管出口端面上的排气压力pe等于临界压力p*,在出口端面上马赫数为1,质量流量率就会达到最大。
(2)收敛-扩散喷管 收敛-扩散喷管中背压的影响如图13-26所示。流过收敛-扩散喷管的流体并不是全部加速到超音速。另外,即使达到超音速,如果背压与喷管的设计压力不匹配,就会发生冲击波。
①p0>pa>p*:收敛-扩散喷管中如果背压大于临界压力,在喷管内全部领域流动为亚音速,流过喷管的流量会小于最大流量。喷管内的排气速度在收敛段逐渐增大,到了喷管喉就会达到音速以下的最大速度,但流过扩散段时会逐渐减小。因此压力在收敛段降低,在扩散段增大。

图13-26 收敛、扩散喷管内的压力分布
②pa=p*:背压等于临界压力时,在喷管喉部分压力会达到临界压力p*,排气速度会达到音速,但是扩散段仅作为扩散管,排气速度会减小到亚音速流动。流过喷管的流量因喷管喉处于临界压力状态,因此会达到最大质量流量率。
③p*>pa>pe:背压小于临界压力,大于喷管设计压力pe时,在喷管喉上达到音速,并在扩散段压力进一步下降,使排气速度加速到超音速。但是,在喷管出口气体继续膨胀,使压力下降到小于背压时会发生逆流,因此在喷管壁面会发生气流剥离,导致发生突然间的不连续压力上升现象,这样的压力不连续点称为正激波。如果发生激波现象,排气速度就会减小到亚音速状态,在正激波下游的喷管扩散段会起着扩散管的作用,使排气速度进一步下降,且压力持续上升。这样的状态是在喷管的膨胀比过大时发生,称为膨胀过度。
④p*>pe>pa:背压小于临界压力和喷管设计压力时,在喷管喉上达到音速,并在扩散段加速到超音速。这样的条件是在喷管长度短,即膨胀比较小的情况下发生,此时排气还能进一步膨胀,称为膨胀不足。因此,燃烧气体离开喷管出口端面时发生急剧膨胀产生斜激波,激波在发动机尾流的边界上被反射,与产生的压力波相互交叉,在下游反复发生压缩和膨胀。即,正激波和斜激波是在背压与喷管设计压力不一致时发生。
引用上述条件,收敛-扩散喷管内的质量流量率如图13-26b所示。区域Ⅰ是收敛段的亚音速喷管领域,区域Ⅱ是音速喷管或超音速喷管的扩散段领域,满足如表13-5所示的条件。
4.临界压力比和最大质量流量率
(1)临界压力比 现在对流过喷管的流量达到最大的临界压力比p*/p0进行计算。这可以通过对流过喷管的质量流量率式(13.68b)的右边(又称为流量函数ν)用压力比p/p0进行微分,用得出的值为0时的压力比来求出。
设定压力比p/p0为r,流量函数ψ可以表示为
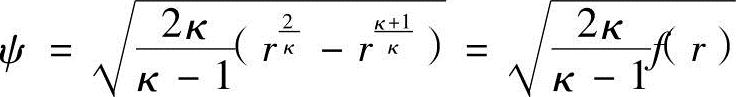
因流量函数ψ最大的压力比r为df(r)/dr=0,可得

式(13.70)为流量函数ψ最大的压力比,即为能流过喷管的最大质量流量率的压力比。在此,把压力比p*/p0称为临界压力比,把压力p*称为相对于喷管入口压力p0的临界压力。
(2)喷管喉部速度 质量守恒式“ 一定”中,如果各端面的状态参数(p、T、ρ等)和质量流量率
一定”中,如果各端面的状态参数(p、T、ρ等)和质量流量率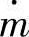 不变,在喷管内端面积A最小的部分速度V会达到最大。在收敛喷管中喷管出口端面,在收敛-扩散喷管中喷管喉端面为最小流动面积。现在求出临界压力比(以上标*表示)条件下的喷管内最小端面部分(喷管喉、以下标t表示)的速度Vt*。这对喷管内速度式(13.66a)中的压力比p2/p0以临界压力比p*/p0式(13.70)代入可以求出。
不变,在喷管内端面积A最小的部分速度V会达到最大。在收敛喷管中喷管出口端面,在收敛-扩散喷管中喷管喉端面为最小流动面积。现在求出临界压力比(以上标*表示)条件下的喷管内最小端面部分(喷管喉、以下标t表示)的速度Vt*。这对喷管内速度式(13.66a)中的压力比p2/p0以临界压力比p*/p0式(13.70)代入可以求出。

式中,对于总温T0应用了式(13.17);Tt*为临界压力比条件下喷管喉部的气体温度。因式(13.71)与音速a相关式(13.6)相同,可以表示为
Vt*=a或Mt*=1 (13.72)
式(13.72)表示在临界压力比条件下,喷管喉部气体的速度Vt*等于音速a,即马赫数Mt*=1。因此,临界压力比p*/p0式(13.70)表示马赫数M=1时的状态参数,临界温度比和临界密度比相关状态方程与前述的式(13.17)和式(13.19)相同。
(3)最大质量流量率 流过喷管的最大质量流量率(或临界流量率) 是对式(13.69a)中的压力比pt/p0以临界压力比p*/p0式(13.70)代入求出的。
是对式(13.69a)中的压力比pt/p0以临界压力比p*/p0式(13.70)代入求出的。
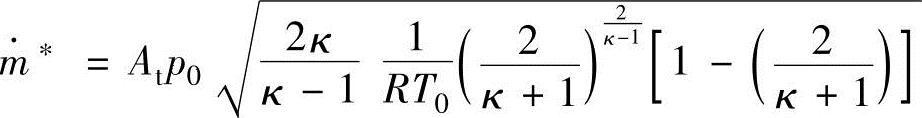

式中,Cm为质量流量系数,表示为

流过喷管的最大流量 根据式(13.73)可知,与喷管入口(燃烧室)的总压p0、喷管喉部端面积At和质量流量系数Cm成正比。
根据式(13.73)可知,与喷管入口(燃烧室)的总压p0、喷管喉部端面积At和质量流量系数Cm成正比。
5.超音速喷管的流动变量
喷管的流动变量为表示燃烧室的总参数(T0、p0、ρ0)与喷管内的任意端面上的静态参数(T,p,ρ)及在此位置上的马赫数M之间关系的函数式,有前述的式(13.11)~式(13.13)。

喷管的流动变量除了上述3种函数外,还有喷管喉部面积和速度与任意端面上的面积和速度之比A/At和V/Vt。
音速流动所需的喷管喉部面积At与喷管内任意端面上的面积A之间,在连续的条件下AρV=AtρtVt成立。引用理想气体状态方程、喷管喉部马赫数Mt=1和等熵流动函数式(13.11)~式(13.13),如下的关系式成立:

根据式(13.75)得知,面积比A/At为马赫数M和质量热容比κ的函数。当质量热容比不变时,由马赫数决定其值。当面积比不变时,马赫数有两个解,这与收敛-扩散喷管会有各1个亚音速和超音速速度的事实相符。
速度比V/Vt也同样与上式一样展开,可得

图13-27所示为质量热容比为κ=1.4时,以部分马赫数M为横坐标的与超音速喷管流动变量之间的关系。如图所示,M<1的领域与亚音速领域的喷管收敛段,M=1为喷管喉部,M>1领域与超音速领域的喷管扩散段(膨胀部分)相对应。当M<0.3时,可以忽略排气的密度、压力、温度的变化,看成非压缩性流动。可以看出,为了获得马赫数M=10的高速流动,需要很大的膨胀比∈,但此时的速度比V/Vt相对来说不很大。
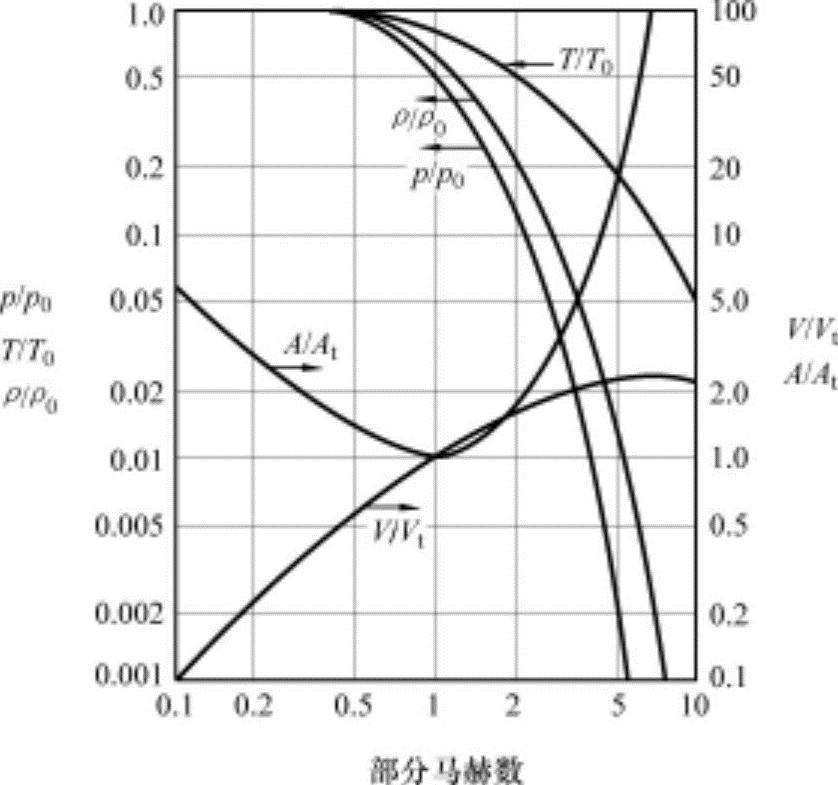
图13-27 收敛-扩散喷管中部分马赫数与流动变量之间的关系
6.喷管膨胀比、速度比
(1)喷管膨胀比 喷管膨胀比在超音速喷管中定义为出口端面积Ae与喷管喉部端面积At之比。喷管膨胀比随喷管设计条件和周围大气条件的改变而发生变化。速度Ve、Vt引用式(13.66),密度引用理想气体状态方程“p-1/κ/ρ=C”,由此可得

(2)喷管速度比 喷管速度比Ve/Vt定义为喷管喉部速度 对喷管出口速度Ve之比,由此可得
对喷管出口速度Ve之比,由此可得

与喷管出口最大速度Ve,max之比为,在式(13.78)中pe=0的状态,即燃烧气体向真空中喷出时的状态,此时的喷管速度比为

因此,燃烧气体的质量热容比为κ=1.4时,上式答案为 ,即喷管出口的最大速度Ve,max为喷管喉部速度Vt(音速,是温度的函数)的2.45倍。这称为喷管的临界马赫数M*,表示临界马赫数为2.45。
,即喷管出口的最大速度Ve,max为喷管喉部速度Vt(音速,是温度的函数)的2.45倍。这称为喷管的临界马赫数M*,表示临界马赫数为2.45。
【例13.1】
质量热容比为κ=1.4,气体常数为R=287J/(kg·K)的空气在内径为0.15m的直管内流动。气体以马赫数1.5并无摩擦地通过收敛-扩散喷管从导管中排出。在喷管入口中压力和温度分别为350kPa、340K,马赫数为0.15。请求出喷管喉部的面积,喷管喉和出口的压力、密度、温度、速度和质量流量率(图13-28)。
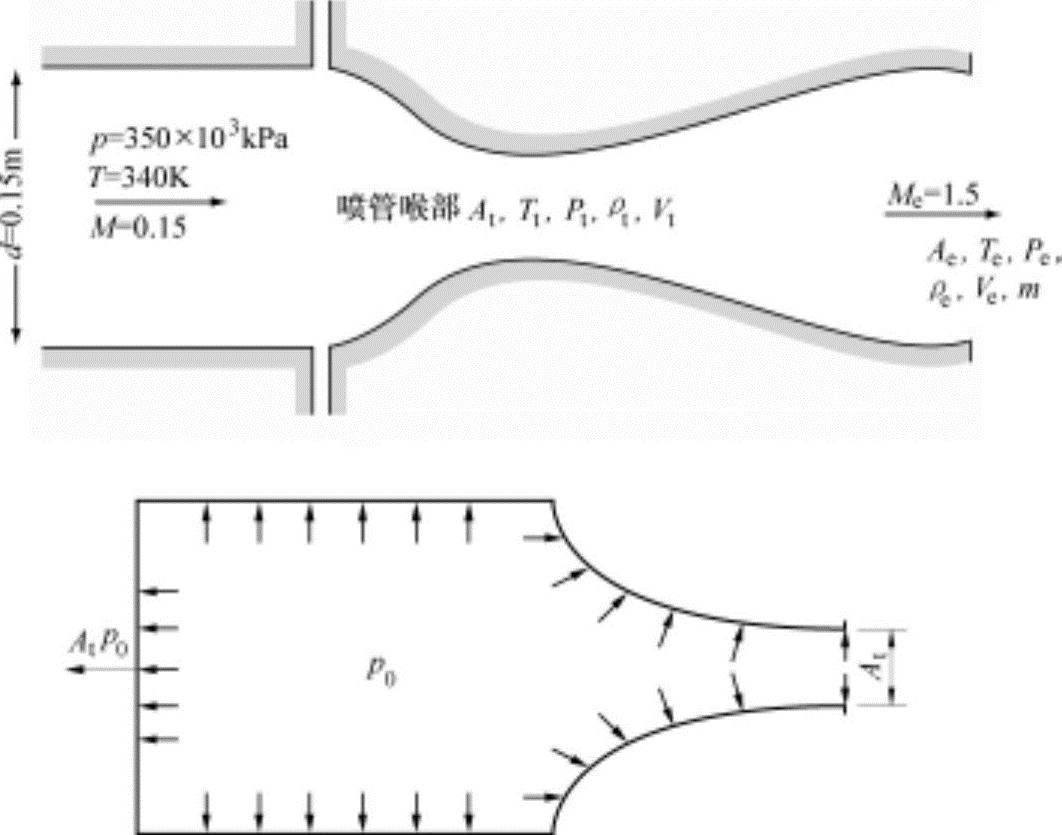
图13-28 Atp0的说明
【解题】
在喷管喉部因马赫数为M=1,喷管喉的状态参数以下标t、出口的状态参数以下标e表示。
喷管喉部的端面积利用端面积与马赫数之间的关系式(13.75),有

代入A=πd2/4=π×0.152/4、κ=1.4、M=0.15,可以得出

根据式(13.11)和式(13.12)可以得出总温和总压为
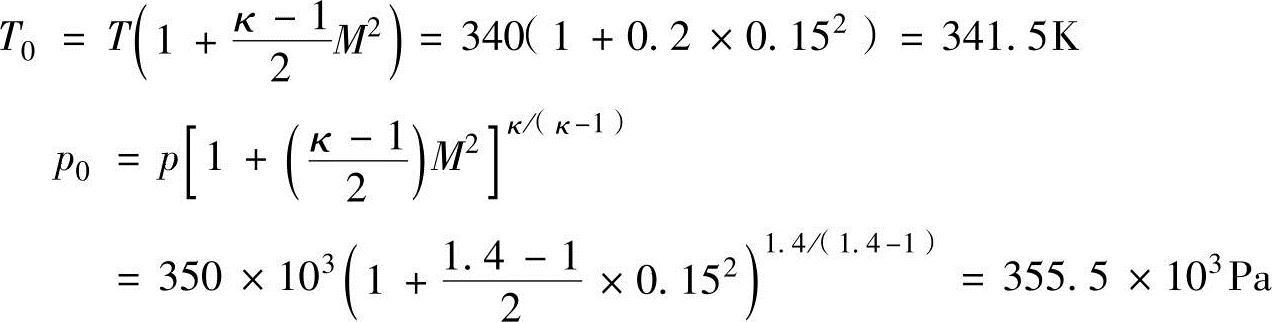
喷管喉部的温度和压力为,因M=1,因此根据式(13.17)和式(13.18)可以得出
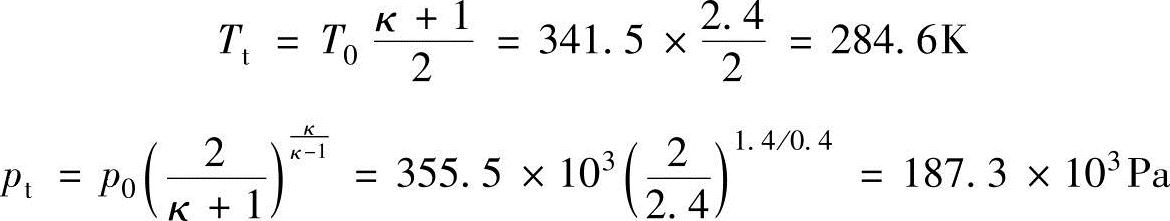
喷管喉部的密度和音速的解为

因此,喷管喉部的气体速度Vt的解为
Vt=ct=338.2m/s
根据式(13.11)和式(13.12),可以得出喷管出口的温度和压力为

密度和音速为
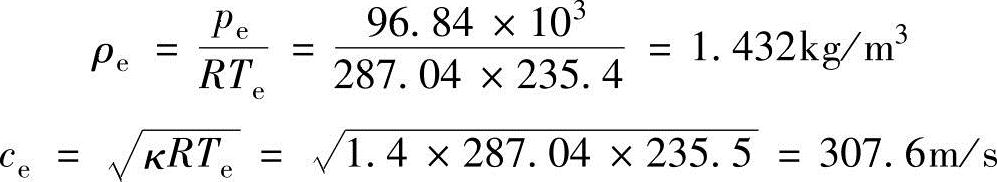
因此,喷管出口空气的排出速度和质量流量率的解为
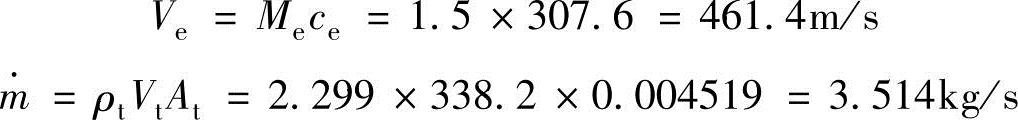
有关内燃机学的文章

柴油燃油压缩为很高的压力,这会影响燃油喷射量,因此这在喷射调节系统中成为应考虑的重要因素。另外,燃油喷射量的改变会带来废气排放量和输出功率的变化。在传统的直列式和分配式燃油喷射系统中,喷射时间以输送时间为依据决定。......
2023-06-28

就这个意义来说,艺术作品的表现愈优美,它的内容和思想也就具有愈深刻的内在真实。只有在最高的艺术里,理念和表现才是真正互相符合的,这就是说,用来表现理念的形象本身就是绝对真实的形象,因为它所表现的理念内容本身也是真实的内容。从此可知,只有真正具体的理念才能产生真正的形象,这两方面的符合就是理想。......
2023-12-06

位置控制式柴油喷射系统是在机械式柴油喷射系统的基础上进行电子技术改造而成,控制喷油量的实质是:控制油量调节滑套(或齿杆)的位移量;控制喷油定时的实质是:控制定时控制活塞的位移量。位置控制式柴油喷射系统虽然只能有限改善柴油机的动力性与经济性,但是,电子调速器和电子提前器在柴油机上的应用,为柴油机电子控制技术的发展奠定了基础。......
2023-09-23

7.3.2.3混合料的配合比与拌制混合料配合比应遵守下列规定:1)干法喷射水泥与砂、石之重量比宜为1.0∶4.0~1.0∶4.5;水灰比宜为0.40~0.45;湿法喷射水泥与砂、石之重量比宜为1.0∶3.5~1.0∶4.0;水灰比宜为0.42~0.50,砂率宜为50%~60%;2)速凝剂或其他外加剂的掺量应通过试验确定;3)外掺料的添加量应符合有关技术标准的要求,并通过试验确定。......
2023-11-04

图13-17 多级火箭的形状3.人造地球卫星的发射把人造地球卫星或其他货物运送到地球同步轨道上的运载火箭通常使用3级液体推进剂火箭。此时第1、2级火箭被分离脱开,仅第3级和人造地球卫星在暂泊轨道上飞行,一旦到达赤道上空,第3级火箭点火并进入转移轨道,之后第3级火箭从卫星上分离出来。......
2023-06-28

按有无控制系统分: 可分为有控制的火箭弹 和无控制的火箭弹。当然, 这些控制技术应以不使火箭弹制造成本过高为限, 否则, 就失去在战场上大量使用的优越性而进入导弹范畴了。 按火箭动力装置所用燃料来分: 可分为液体燃料火箭弹和固体燃料火箭弹。 按射程范围分: 可分为近程火箭弹、中程火箭弹、远程火箭弹和超远程火箭弹。 按飞行稳定方式分: 有靠高速旋转保持飞行稳定的涡轮火箭弹和靠尾翼保持飞行稳定的尾翼火箭弹两种。......
2023-06-15

固体火箭发动机构件的接头形式尺寸如图4-2-38所示。图4-2-38 火箭发动机壳体焊接接头2)提高加速电压:提高加速电压Ua,进一步提高电子束焦点的功率密度,从而使热影响区的软化带宽度更窄。发动机壳体焊接接头的抗拉强度为1.78GPa,接头抗拉强度降低4%左右。国外同类钢种42Cr2MnSiNiMo厚度为4.5mm,淬火态试件真空电子束焊时,抗拉强度和接头强度分别下降22%和6%。表4-2-8 发动机壳体电子束焊焊接参数......
2023-06-26
相关推荐