多级火箭: 发射人造卫星的液体推进剂技术

2025-09-29 理论教育版权反馈

【摘要】：图13-17 多级火箭的形状3.人造地球卫星的发射把人造地球卫星或其他货物运送到地球同步轨道上的运载火箭通常使用3级液体推进剂火箭。此时第1、2级火箭被分离脱开，仅第3级和人造地球卫星在暂泊轨道上飞行，一旦到达赤道上空，第3级火箭点火并进入转移轨道，之后第3级火箭从卫星上分离出来。

多级火箭是在没有不现实地加大质量比R（=m₀/m_f），也没有减小运输能力的状态下获得高燃烧速度的方法。

1.运载火箭起飞速度

火箭能脱离地球引力场所需的初速度，可以用反向思维，求出从地球引力场外部向地球自由落体的物体在地球表面上的速度即可。

在离地球中心高度r（=R+h）的位置，质量为m的物体自由落体时，其速度变化为由势能转换为动能的结果，具有如下关系：

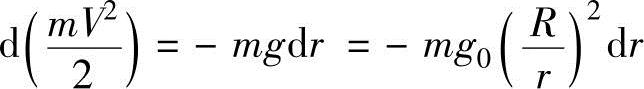
把上式从无限距离（r=∞）到地球表面（r=R）进行积分，推导出

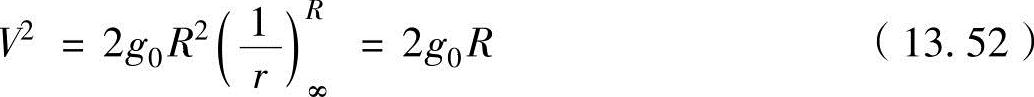
地球半径为6370km，则地球表面的速度为

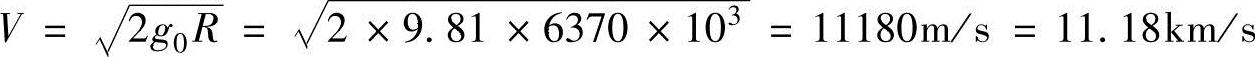
这表示火箭在地面上最小要以此初速度发射，才能脱离地球的引力场。这仅为理想的理论计算值。

现在要求出火箭的速度。通常，质量比MR（=1/R）界限值为0.05，把此值代入式（13.36a）可获得V_f=-cln（0.05）=2.996c，火箭能获得的最大飞行速度是有效排气速度c的3倍左右。但是因有效排气速度为c=I_sg₀，如果固体推进剂火箭与液体推进剂火箭的比推力各自为250s、350s，则最终速度为

固体推进剂火箭：V_f=-（I_sg₀）ln（MR）=-（250×9.8）ln（0.05）=2.45（km/s）

液体推进剂火箭：V_f=-（I_sg₀）ln（MR）=-（350×9.8）ln（0.05）=3.43（km/s）

由上得知，如果质量比为0.05的火箭能获得的速度最大约为4km/s，仅为火箭脱离地球速度（排气喷出速度）12km/s的1/3左右。这表示利用1级火箭不能获得脱离大气层的速度。在1级火箭中，质量比MR=0.05时，推进剂质量占火箭全质量的95%，剩余的5%为结构物和有效载荷的质量，即便如此也很难实现脱离大气层。例如：对V2火箭来说，推进剂占全质量的69%，气体排出速度c为2136m/s，火箭的速度V为1500m/s，速度比ν（=V/c）仅为0.70。

2.多级效果

对于多级火箭来说，各级的初始速度会成为全级的最终速度。多级火箭的最终速度是各级火箭最终速度之和，即n级火箭的最终速度V_f可以表示为

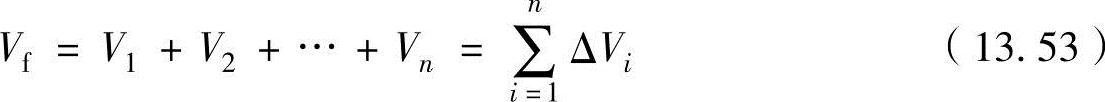
如果没有重力和大气阻力，各级的增加速度可以利用式（13.36a）V_i=-c_iln（MR）_i得出，如果所有各级的有效排气速度c_i相同，n级火箭的最终速度可以表示为

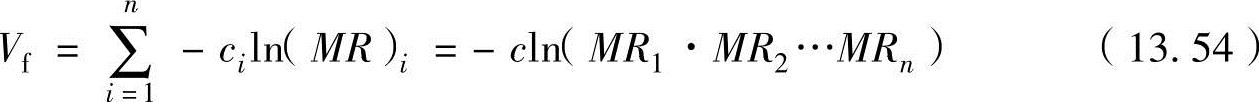
现在对3级火箭的多级效果进行分析。当发射3级火箭达到最高速度时，分离第1级火箭，同时第2级火箭点火产生推力。与此相同，当第2级火箭达到最高速度时，第3级火箭点火，同时分离第2级火箭。假设发射初期的推进剂重量占全重量的75%（μ=0.25），从图13-16中得知速度比ν为1.4，火箭的速度V为排气速度c的1.4倍。实际上因存在喷管的膨胀损失和摩擦等损失，速度比ν会比理论值小，如果假设ν=1，因碳氢燃料的排气喷气速度约为4000m/s，所以此第1级火箭也能达到与此相同的速度。(https://www.chuimin.cn)

对第2级火箭来说，对式（13.34b）中设定初始值t=0时为m=m₀₂、V=V₁，并到任意时间t为止进行积分，有

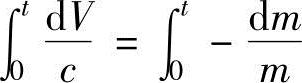
由此可得

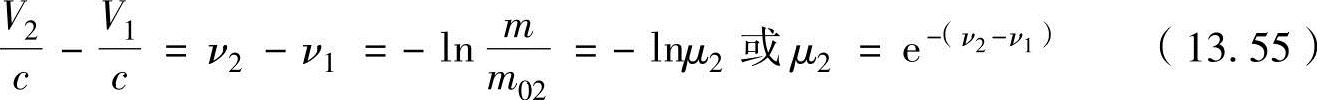
式中，m₀₂为第2级火箭的初始质量（1级火箭的最终质量），μ₂、ν₂分别为第2级火箭的质量比和速度比。式（13.55）的关系在图13-16中把μ引用为μ₂、ν引用为（ν₂-ν₁），同样以质量比μ的曲线得出。与第1级原理相同，第2级火箭也在μ2=0.25时ν₂-ν₁=1.4，因存在各种损失，假设ν₂-ν₁=1，即ν₂=ν₁+1=2，以此第2级火箭的最高速度V₂为8000m/s左右。同理，第3级火箭的最高速度V₃为12000m/s左右，因此最终达到脱离地球引力场的速度。

假设火箭的各级最终重量的15%为结构物重量m_s，10%为有效载荷重量m_pl。如果第3级火箭的有效载荷质量为100kg，第3级火箭的初始质量为1000kg，第2级火箭的有效载荷质量为第3级火箭质量，以此第2级火箭的初始质量为10000kg，以此类推，第1级火箭的初始质量为100000kg。从而3级火箭的初始有效载荷比为100/100000=0.001，说明有效载荷比数值很小。

理论上，虽然火箭的级数越多其飞行性能越会提高，但是一旦级数达到一定程度，其飞行性能的提高会达到饱和状态。另外，级数的增加会带来结构的复杂性，并在可靠性等方面会出现很多问题。目前，最多使用的是3级火箭，侦察兵（美国）和SLV（印度）等4级固体推进剂火箭发动机也有，但没有采用更多级的火箭。多级火箭相关例子如图13-17所示。

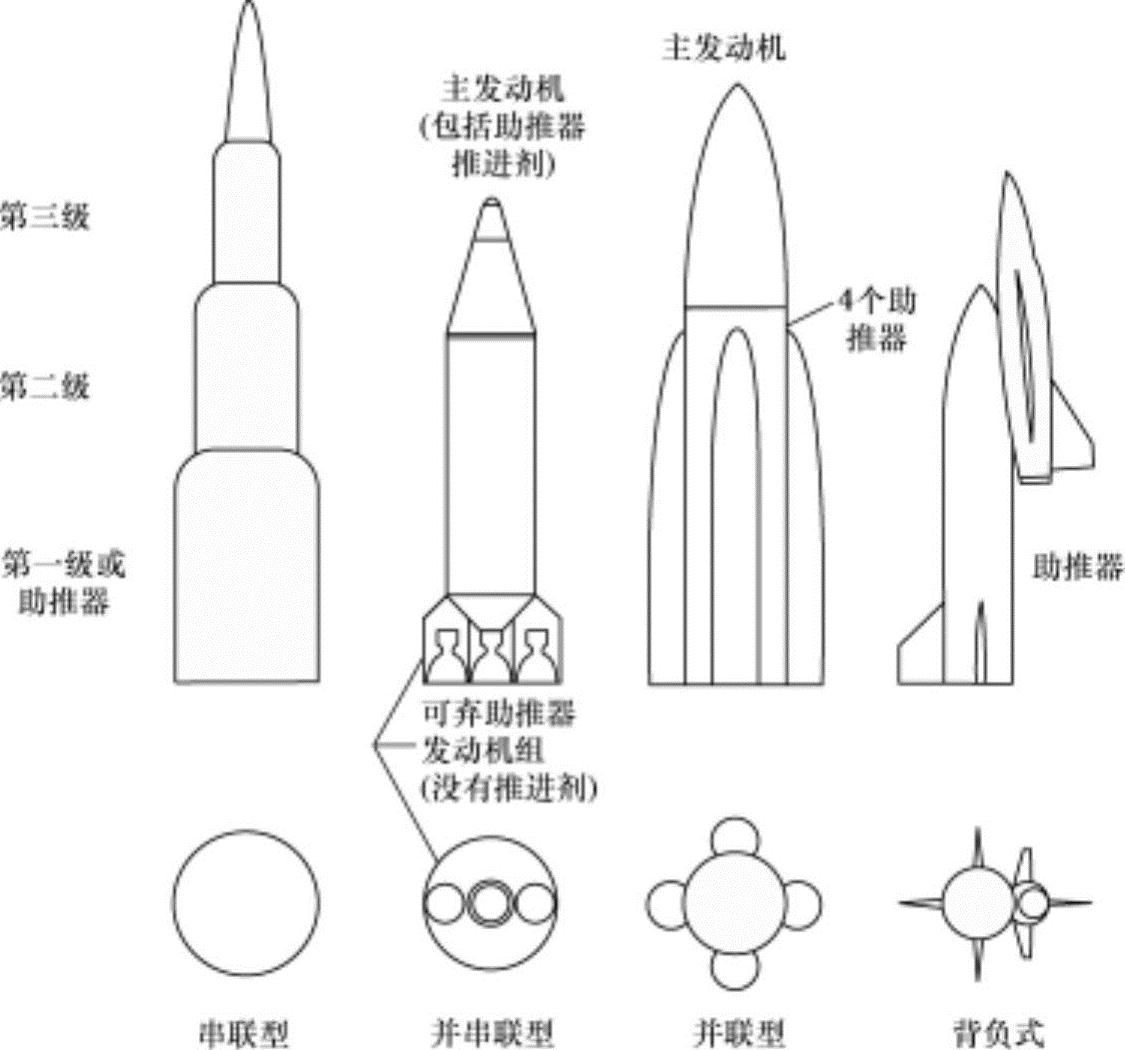
图13-17 多级火箭的形状

3.人造地球卫星的发射

把人造地球卫星或其他货物运送到地球同步轨道（GEO）上的运载火箭通常使用3级液体推进剂火箭。有时为了提高发射能力，在第1级火箭上附加3个、6个、9个固体推进剂助推器（SRB），以增加起飞时的推力。

发射人造地球卫星时，为了充分利用地球的自转能量，大部分向着东方发射。运载火箭进入地球同步轨道的飞行路径如图13-18所示。运载火箭通过强劲的第1级起飞加速，当第2级点火时会穿过地球大气层上升到约200km高度进入到暂泊轨道（Parking orbit）。此时第1、2级火箭被分离脱开，仅第3级和人造地球卫星在暂泊轨道上飞行，一旦到达赤道上空，第3级火箭点火并进入转移轨道，之后第3级火箭从卫星上分离出来。第3级火箭的发射点处于转移轨道近地点，因此第3级火箭起着近地点推进发动机（PKM）的作用。卫星在转移轨道上旋转几圈收集轨道数据后，通过远地点推进发动机（AKM）的发射向着目的地方向变更姿态。

人造地球卫星中配备有十几个姿态控制用推进器。远地点发动机往往直接附加在人造地球卫星上，一旦卫星到达适当的远地点位置，远地点发动机（AMF）点火，卫星进入接近GEO的漂移轨道，之后AKM从卫星上分离出来。漂流中的卫星通过几个推进器的反复操作，调整卫星的姿态和移动轨道，直到到达目标位置并稳定为止。

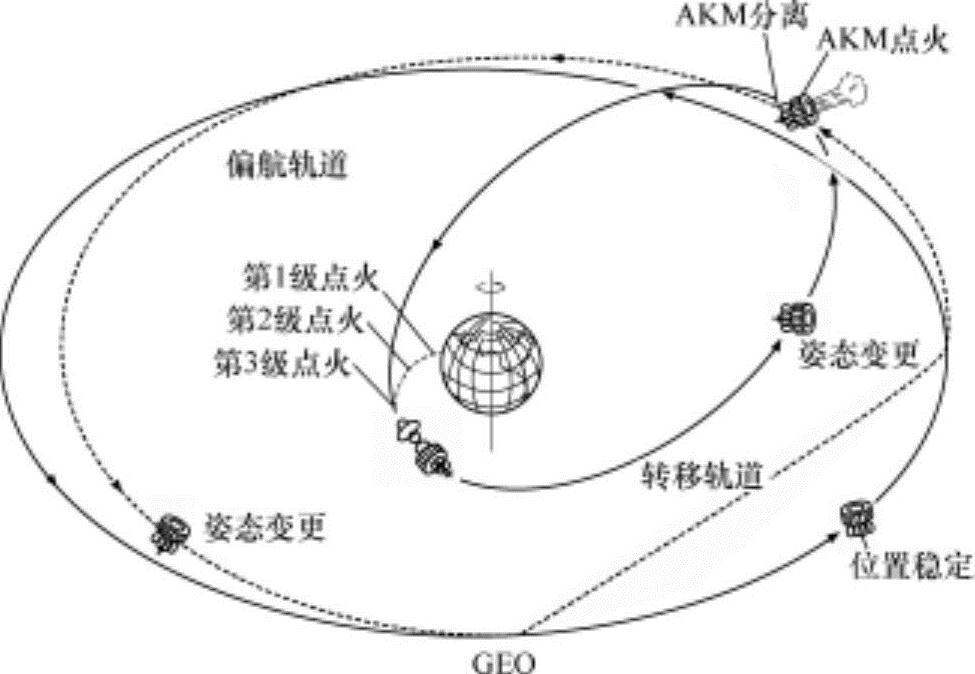
图13-18 通过运载火箭的进入GEO的过程

如图13-19所示为阿利安-44L为了进入地球同步转移轨道（GTO）的第1级火箭点火并起飞到运载火箭任务结束为止的一系列飞行计划（飞行顺序、飞行时间、飞行状态）。

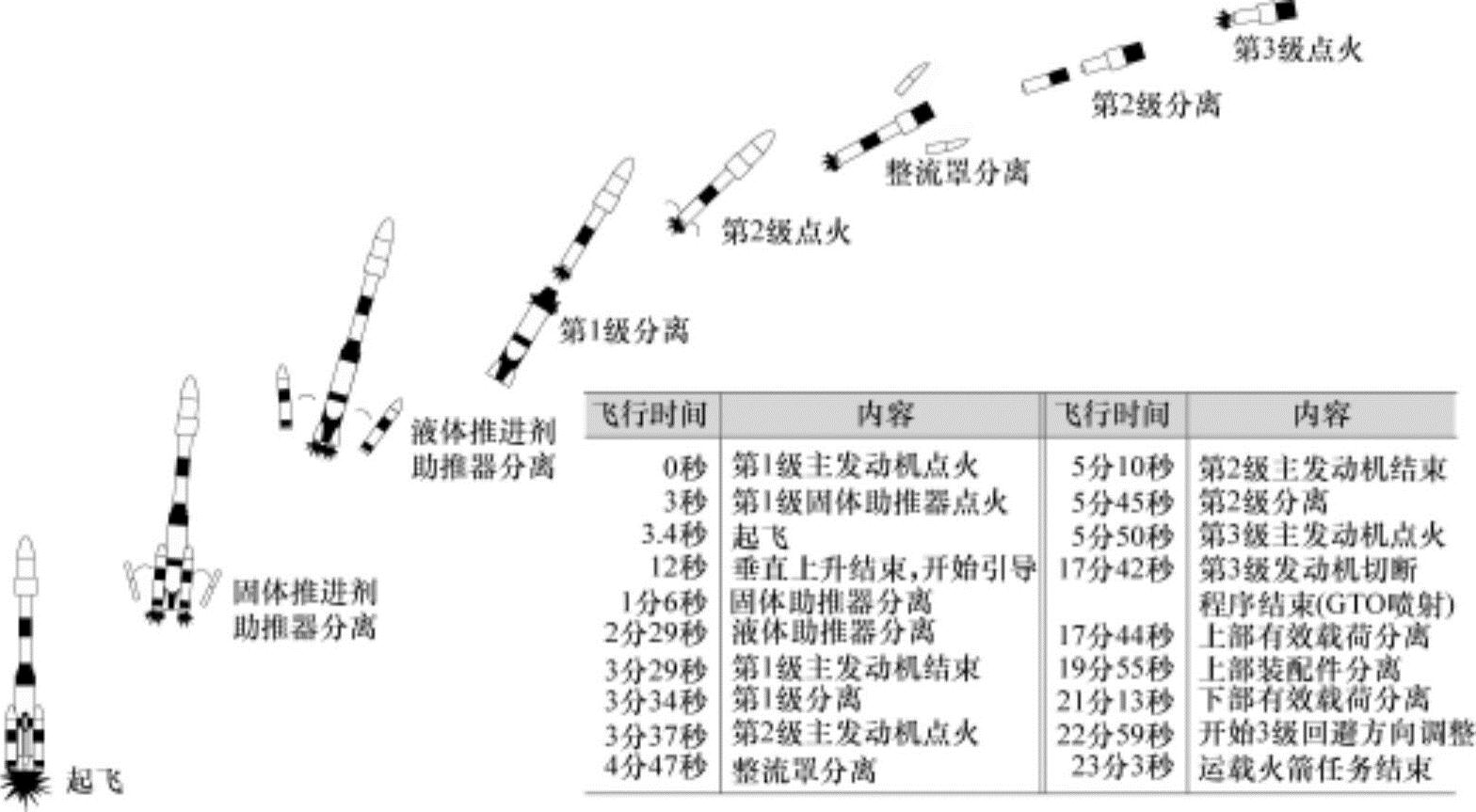
图13-19 阿利安-44L的典型飞行概略

多级火箭: 发射人造卫星的液体推进剂技术

相关推荐