从动件上升的最大位移用h表示，称为行程。凸轮继续转动，由于与从动件尖顶接触的凸轮轮廓向径逐渐变小，从动件返回，这一过程称为回程，对应的凸轮转角δ′0称为回程运动角。图1-28 凸轮机构的工作过程a）凸轮机构 b）位移线图2.从动件常用运动规律等速运动规律 当凸轮以等角速度ω转动时，从动件在推程或回程中的速度保持不变，称为等速运动。因此，等速运动规律只适用于低速、轻载的场合。......
2025-09-29
在重力场中的运动规律
【摘要】：重力场中的火箭运动存在重力损失mgsinθ和空气阻力损失D。因而在重力场中火箭的运动方程式为式中，m为火箭质量。式可以用与式和式相对应的无量纲式表示。式与无重力场式相比，可以看出仅增加了右边最后项。因此，当高度为h=100km时，把这些已知的数据代入式中，可以得出重力加速度为g≈9.48m/s2，这是地球海平面上的97%左右。即，从地面到100km高度的重力变化仅减小3%，因此在推进剂燃烧期间将重力加速度可以看成g常数也无妨。
重力场中的火箭运动存在重力损失mgsinθ和空气阻力损失D。
1.火箭的运动方程式
为了简单推导出火箭的运动方程式，首先忽略空气的阻力，并假设为火箭发射后立即垂直方向上升，sinθ=1，重力加速度为常数。因而在重力场中火箭的运动方程式（13.32）为
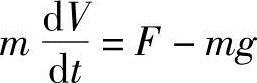
式中，m为火箭质量。在推力F=kc中，把推进剂消耗率k（kg/s）引用火箭的质量损失率，即k=-dm/dt，上式改写为
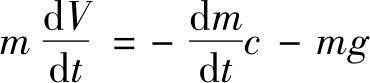
为了对上式进行积分，转换为如下形态：
把上式以式（13.34b）相同的条件进行积分，并引用前述符号进行转换，
可得
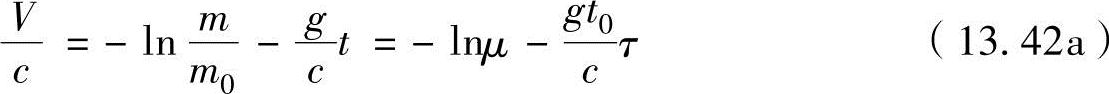
或
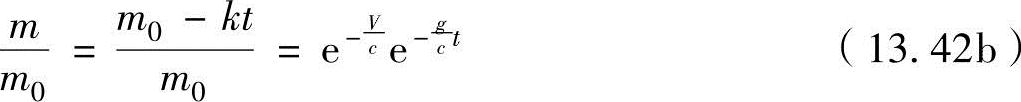
式（13.42b）就是火箭在重力场中的运动方程式。此方程式与在无重力场中的火箭运动方程式（13.35b）不同的是，仅多出了因数e-gt/c。此因数的值始终小于1，因此如果假设通过燃烧的推进剂质量减小量κt相同，那么对于火箭的速度V，时间t越短，即因数e-gt/c的值越接近1就会越大。这表示燃料消耗率κ越大和燃烧时间t越短越好。极限状态下最好是所有推进剂瞬间燃烧结束，此时的质量比μ与速度比ν之间的关系可以利用重力加速度g=0（无重力场状态）的条件得出，如图13-15所示。
但是，在实际燃烧过程中燃烧速度的大小具有局限性，并且还存在到目前为止还没有考虑过的火箭空气阻力，因此火箭在发射后并不是立即加速到最高速度，而是在空气密度较大的低空缓慢增加速度，到达空气密度相对较小的高空后再加速到最高速度飞行。
式（13.42a）可以用与式（13.38）和式（13.40b）相对应的无量纲式表示。
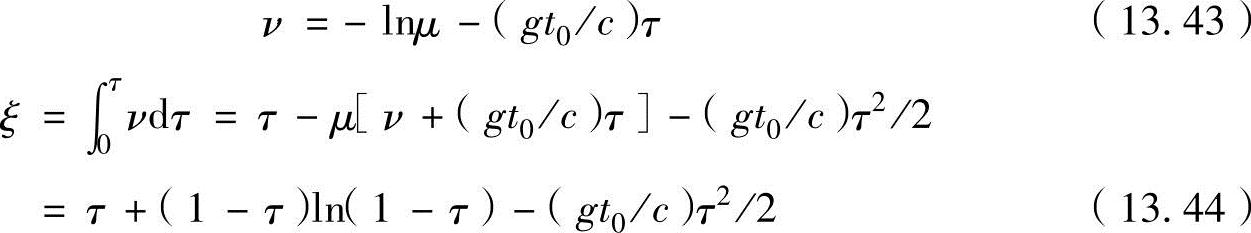
式（13.44）与无重力场式（13.40a）相比，可以看出仅增加了右边最后项。上述两个式仅在推进剂全部燃烧时成立，表示在推进剂比ζ（=mp/m0）不变的条件下，燃烧结束时的最终速度与高度之间的关系。因燃烧结束后没有推进力，火箭仅按照自由落体运动定律运动。
现在计算一下重力场中火箭的最终速度Vf。对此，把式（13.41）进行积分到推进剂完全燃烧的时间tb为止，因在时间t=0时为m=m0、V=0，在时间tb时为m=mf、V=Vf，因此可以用下式进行计算得出。
Vf=clnR-gtb （13.45）
式中，R（=1/MR）为以m0/mf定义的质量比。可以看出火箭的速度Vf随燃烧时间tb的缩短而增加。
燃烧结束时的高度hb可以用下式进行计算得出。(https://www.chuimin.cn)
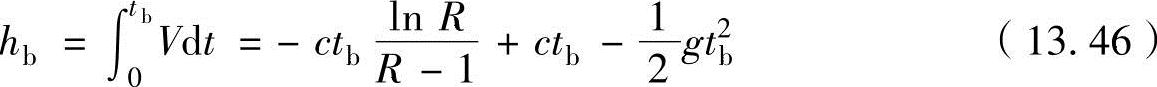
火箭的最大上升高度hmax可以利用在燃烧结束时的动能与势能相等的关系进行计算。
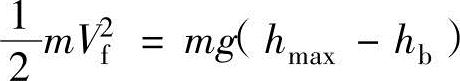
在最终速度Vf中代入式（13.45），hb中代入式（13.46），可得
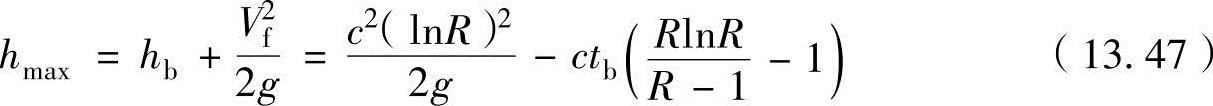
当质量比R保持不变时，燃烧结束时的速度Vf越大或燃烧时间tb越短，火箭的最大上升高度hmax就会越高。另外，如要增加燃烧速度，质量比R要非常大，质量比大表示火箭的最终质量mf小，这表示火箭的运输能力（有效载荷质量）降低。因此，质量比的大小也有局限性。
2.重力的影响
根据万有引力定律，行星吸引火箭（航天器）的力量F与两个物质的质量M、m的之积成正比，与两个物质之间的距离成反比，其计算式为
式中，比例常数G为重力常数6.67259×10-11N·m2/kg2。引用力F=ma和式（13.48），在质量为M、半径为R的行星表面重力加速度g0，以及在高度为h（或r=R+h）的高度上重力加速度的计算式为
根据式（13.49），重力加速度g与行星表面上的重力加速度g0之间具有如下的关系：
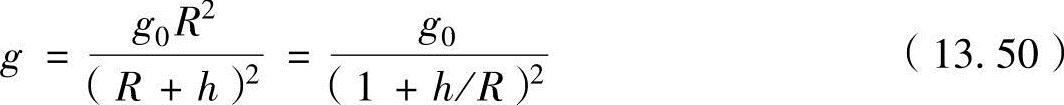
式中，g0为地球表面的重力加速度9.81m/s；R为地球半径6370km。因此，当高度为h=100km时，把这些已知的数据代入式（13.50）中，可以得出重力加速度为g≈9.48m/s2，这是地球海平面上的97%左右。即，从地面到100km高度的重力变化仅减小3%，因此在推进剂燃烧期间将重力加速度可以看成g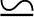
常数也无妨。
实际火箭的设计要考虑空气阻力，在密度较低的高度以不太大的适当速度飞行，在空气密度相当小，即空气阻力很小的高高空中，使飞行速度达到最高。
3.空气阻力损失
火箭的空气阻力可以表示为
式中，CD为阻力系数；ρ为空气密度；V为火箭速度；A为火箭前方受风端面积。阻力系数与火箭的形状、速度（马赫数）、火箭的飞行方向角度等有关。尤其是，空气密度随火箭的飞行，即随高度的升高发生很大的变化。在32km左右的高度上空气密度约比海平面减小1%左右。
空气阻力D与速度平方V2成正比，因此火箭速度增加时，阻力损失会大幅度增大。虽然减小速度会大幅度降低阻力损失，但是如果减小发射速度，则会增加发射时间，导致重力损失增大。
相关文章
- 详细阅读
-
刚体在平面的运动方程详细阅读
刚体上与平面Ⅱ相交的部分，称为“平面图形”，用S 表示。根据平面运动的特征，当刚体做平面运动时，平面图形S 上各点始终在平面Ⅱ运动。为研究平面图形S 在其自身平面内的运动，在此平面内建立静坐标系Oxy。式称为“刚体平面运动方程”。......
2025-09-29
-
凸轮机构及从动件的运动规律分析详细阅读
(一)凸轮机构的组成、功用及分类凸轮机构在纺织机械中应用相当广泛。通过凸轮运动曲线的设计，可以达到所要求的各种运动方案，并且结构紧凑。凸轮机构是主要由凸轮、从动件和机架组成。图2-23盘状凸轮机构按凸轮的形状分，凸轮可分为盘形凸轮、圆柱凸轮和移动凸轮，如图2-24 所示。(二)纺织机械中从动件运动规律的选择1.凸轮机构运动线图 从动件的运动规律是指从动件的位移、速度、加速度随凸轮转角的变化规律，如图2-25 所示。......
2025-09-29
- 详细阅读
-
推移质颗粒单步运动的统计规律分析详细阅读
分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。......
2025-09-29
-
热力学：热运动的宏观规律与热机的工作原理详细阅读
热力学是热运动的宏观理论，它主要讨论热现象的基本规律，其特点是以实验事实为依据，不考虑物质的微观结构。在热机中，有的热机中流体是在封闭的管道中循环，如核反应动力装置中的循环流体；而有的热机则以大气为冷凝器，管道是开放的，如内燃机等。起初人们误认为布朗运动是由外界影响引起的。因此，组成物质的分子，在永恒地做无规则运动，是物质系统热运动的微观实质。分子无规则运动的剧烈程度，随温度升高而增强。......
2025-09-29
-
滚动轴承中的运动关系简介详细阅读
滚动轴承是承受载荷而又旋转的元件组合。为了分析轴承的运转情况，必须了解轴承中各元件间的相对运动关系。同理可求出保持器相对于外圈的转速为nce=nc-ne=-nec滚动体自转转速nw 此转速是相当于保持器转速为零时，滚动体围绕其自身中心轴线的转速，可由接触点处两物体线速度相等的关系求出。在高速轴承中，还应考虑惯性力矩和摩擦力矩对轴承各元件运动的影响。......
2025-09-29
-
运动中工件的抓取技巧详细阅读
相对于固定工件的抓取，在运动中抓取工件时有一些特殊的考虑。这被称为输送系统和上下料系统之间的同步运动。图3.118错误同步中工件抓取点的偏移关闭机械手时，手指随工件移动，直到工件在机械手中居中，并发生的位置偏移补偿d。所提出的情况清楚地表明，机械手在工件上的精确定位对于成功地在运动中进行抓取操作至关重要。这些发现可用于为传送带搬运中异常快速的抓取操作等情况创建可靠的设计。......
2025-09-29
相关推荐