无重力场中的物体运动探究

2023-06-28 理论教育版权反馈

【摘要】：在无重力场中，因空气阻力D和重力相关力mgsinθ不存在，因此式成为式中，推力F为有效排气速度c（m/s）与航天器的质量损失率k之积。式就是在无重力场中火箭的运动方程式。图13-16 无重力场中火箭的飞行性能在13.4.3节中会进行详细说明，可以看出推进效率在速度比ν=1时为ηp=1，但平均推进效率ηpm并不是与此相同。

运载火箭的飞行性能和轨迹如图13-14所示，如果假设推力方向与飞行方向相同，则如下平衡式成立：

式中，F为推力；D为空气阻力；m为航天器的总质量；V为航天器的速度；g为重力加速度。

在无重力场中，因空气阻力D和重力相关力mgsinθ不存在，因此式（13.32）成为

式中，推力F（N）为有效排气速度c（m/s）与航天器的质量损失率（推进剂消耗率）k（kg/s）之积。航天器的质量损失率可以表示为

把上式代入式（13.33）中，可得

图13-14 航天运载火箭的飞行

为了对上式进行积分，改写为如下形式：

对式（13-34b）进行积分，假设在时间t=0时航天器的初始质量m=m₀、初始发射速度V=0，任意时间t时为m=m、V=V，可得

因此，有

式中，μ=m/m₀，为质量比，ν=V/c，为速度比。式（13.35）就是在无重力场中火箭的运动方程式。当速度比ν=1时，即飞行速度V与有效排气速度c相同时，质量比μ为e^-1。即m/m₀=1/e、（m₀-m）/m₀=1-1/e，因此推进剂的燃烧量（m₀-m）为初始质量m₀的1-1/e=1-1/2.718=0.6321（63.2%）倍。另外，火箭的飞行速度V为气体喷出速度c的ν倍时，因m/m₀=e^-ν，此时火箭的质量m（=m₀-kt，火箭的初始质量m₀减去已经消耗的推进剂质量kt的值）为初期质量m₀的1/e^ν倍。

如果积分区间定为推进剂完全燃烧时的时间t_b为止，m=m_f、V=V_f，即成为火箭最终质量m_f和最终达到速度（燃烧结束速度）V_f，表示为

因此，有

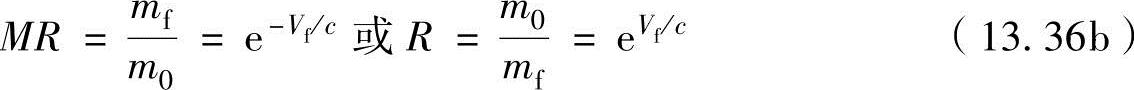
式（13.36b）就是表示有效排气速度c（=g₀I_s）、质量比MR（=1/R）、最终达到速度V_f之间关系的火箭飞行的基本关系式，称为齐奥尔科普斯基方程，如图13-15所示。

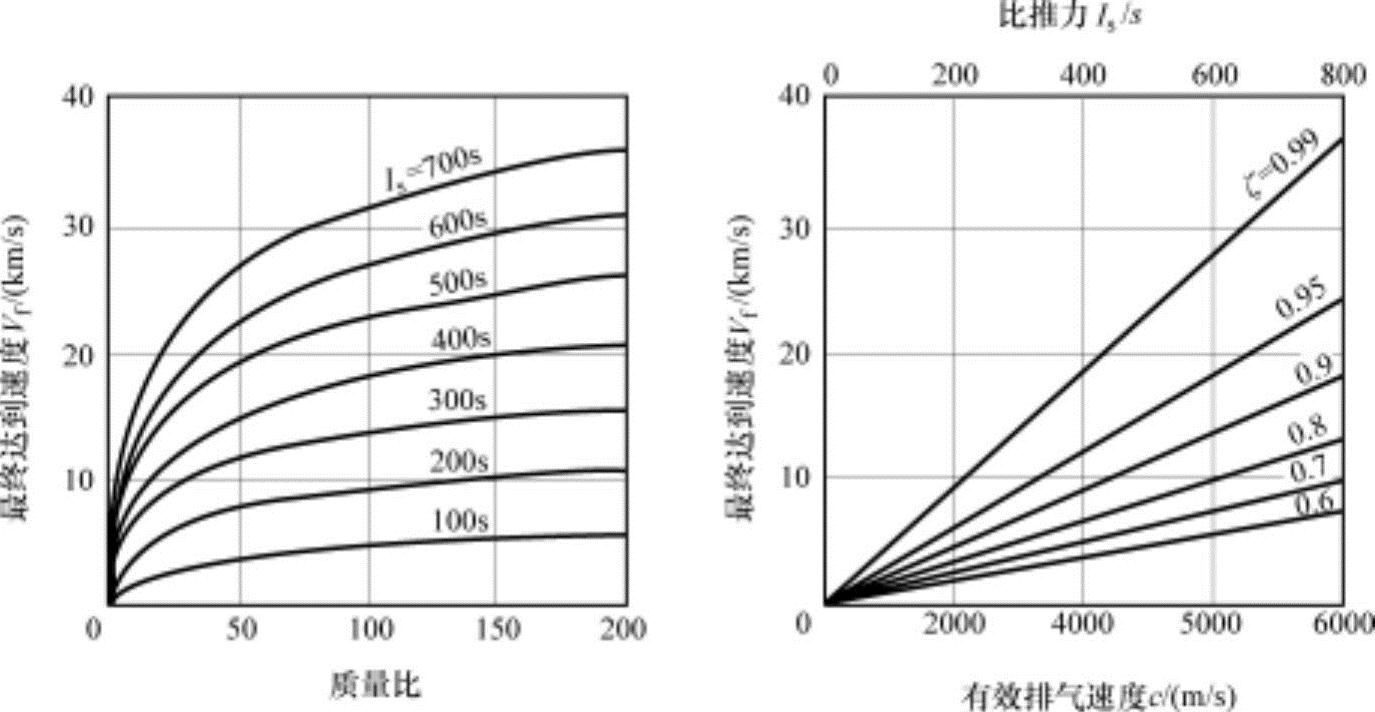
图13-15 质量比、有效排气速度和最终达到速度之间的关系

把平均推进效率η_pm定义为在时间t时火箭的动能与到时间t为止喷出气体量（推进剂的燃烧量）的动能之比。这不是时间t时的推进效率，而是从发射开始到时间t为止的平均推进效率。

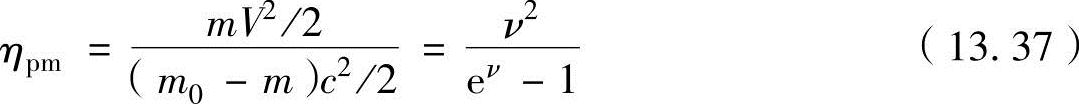
根据质量比为μ=m/m₀=1-kt/m₀=1-t/t₀的关系，把式（13.35a）整理为速度比ν相关式，为

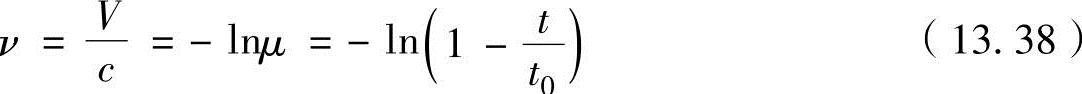
即可以把速度表示为时间的函数。因为飞行里程为，可以表示为

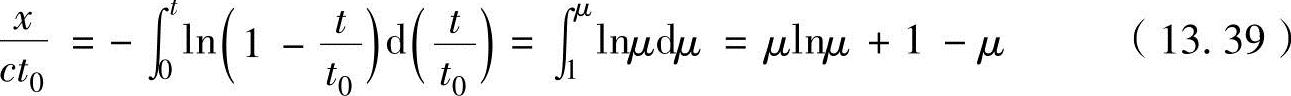
从式（13.39）中推导无量纲飞行里程ξ和无量纲时间τ的公式为

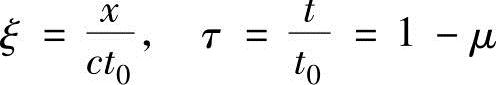
对于无量纲飞行里程ξ，引用式（13.39）和无量纲时间τ，可以推导出

ξ=τ+μlnμ=τ+（1-τ）ln（1-τ）（13.40a）

或，如果引用式（13.38），可以表示为

ξ=τ-μν （13.40b）

在式（13.40b）中，各自代入ξ、τ、μ、ν变量式，可得

式中，推进剂消耗率有k=-dm/dt的关系，因此引用了t₀=m₀/k的关系。

如图13-16所示为相对于速度比ν=V/c的质量比μ=m/m₀、平均推进效率ηpm、无量纲火箭飞行时间τ=kt/m₀、无量纲火箭飞行里程ξ=kx/（cm₀）。从图中可知，平均推进效率在速度比为ν=1.593的位置出现了最大值0.648，此时的质量比为μ=0.203。另外，平均推进效率在速度比为ν=0.7～3的范围内良好。

图13-16 无重力场中火箭的飞行性能

在13.4.3节中会进行详细说明，可以看出推进效率在速度比ν=1时为η_p=1，但平均推进效率η_pm并不是与此相同。另外，对于燃料的燃烧，通过式（13.35b）可知，火箭内剩余的推进剂质量随着速度比ν的增加会急剧减小，火箭速度要达到比气体的喷出速度高出很多的高速并不是那么容易做到的。因此，在实际应用中大体上速度比约为2以下的范围。

无重力场中的物体运动探究

相关推荐