如图7-14所示，考虑了总电动斥力矩对导电斑点半径的影响后，各相中间动导电杆电流峰值增大，外侧动导电杆电流峰值减小，A相电流峰值呈不对称凸形分布，B相和C相电流峰值虽仍然呈现斜坡分布，但斜坡斜率变小。在电动斥力矩和软连接力的共同作用下，各动导电杆总电动斥力矩普遍增大，如图7-17所示。......
2025-09-29
音速与面积的关系：探究声音传播的规律
【摘要】：设定压力为密度和熵的函数p=p（ρ，s），对此进行微分可得对于上式，如果引用等熵流动过程，因ds=0，因此第2项为0，对于右边第1项因从式中得知s=a2，因此可以改写为dp=a2dρ 从式可得在上式的dp中代入式，可得或在式中代入上述中的dp/ρ，可得式与式是具有重要意义的方程式，表示在亚音速和超音速流动中端面积、速度、压力之间的关系完全不同的状态。式的左边端面积的变化dA为负，因此右边也应为负。
非压缩性流体流动时，当端面积减小时，流体的速度增加，当端面积增大时，流体的速度减小。压缩性流体流动时，这样的关系始终不会成立的。
如图13-12所示，对不等端面积管内流动的一维正常状态等熵过程进行分析。在正常状态下，质量流量率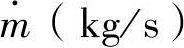
保持不变，连续方程式如下。
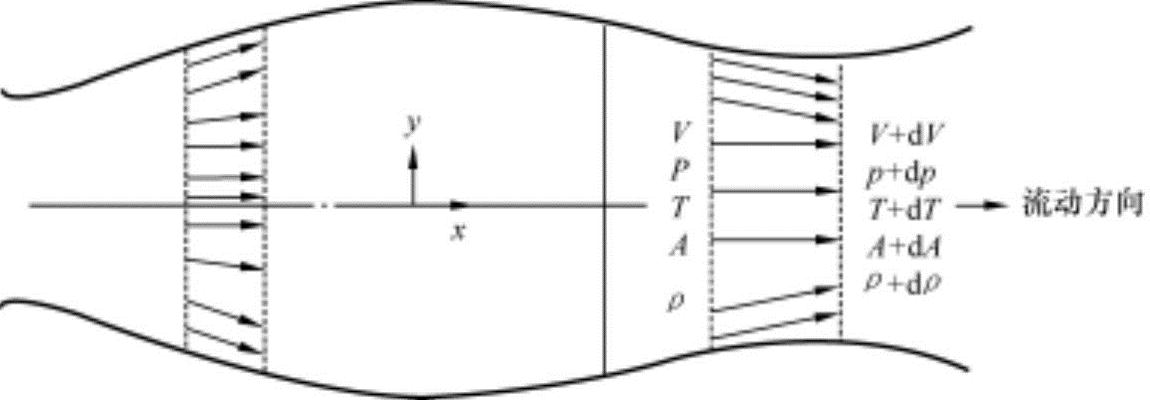
图13-12 管内流动
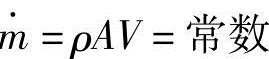
对上式进行微分，并两边用ρAV相除，得
把对管内流动的正常状态能量守恒方程以微分形态表示为
dh+VdV=0
对第2Tds方程式如果引用等熵过程，因ds=0，可以表示为
dh=vdp
把上述2式合并，有
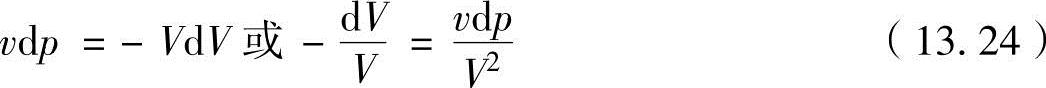
在式（13.23）中引用式（13.24），可得
在等熵过程中，理想气体状态方程“p（1/ρ）κ=C”可以改写为
lnp+κln（1/ρ）=lnC
把上式进行微分可得
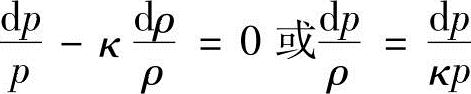
在式（13.25）中如果引用上式和音速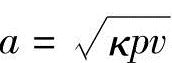
、马赫数M（=V/a），可得
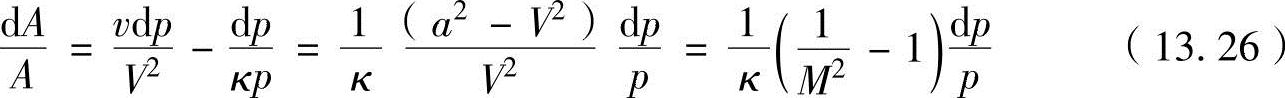
式（13.26）是在端面积不等的流体流动中，表示端面积A、音速M、压力p之间关系的很重要的关系式。
下面推导出类似于式（13.26）的关系式。设定压力为密度和熵的函数p=p（ρ，s），对此进行微分可得(https://www.chuimin.cn)
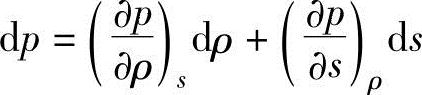
对于上式，如果引用等熵流动过程，因ds=0，因此第2项为0，对于右边第1项因从式（13.5）中得知（dp/dρ）s=a2，因此可以改写为
dp=a2dρ （13.27）
从式（13.24）可得
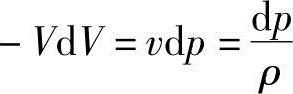
在上式的dp中代入式（13.27），可得
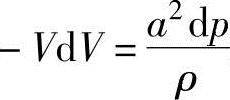或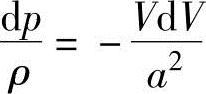
在式（13.23）中代入上述中的dp/ρ，可得
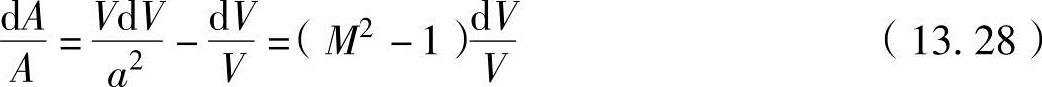
式（13.28）与式（13.26）是具有重要意义的方程式，表示在亚音速和超音速流动中端面积、速度、压力之间的关系完全不同的状态。
1.亚音速流动
喷管是降低流体压力（dp<0）并增大速度（dV>0）的装置。首先对亚音速M<1喷管的端面积如何发生变化进行分析。因为喷管的dV为正（+），在M<C的亚音速流动中，式（13.28）右边括弧内的项为负（-），右边为负。因此，左边也应为负，故dA<0，即A2<A1。这表示在亚音速流动条件下逐渐增速的喷管形状为，端面积向着气体流动方向逐渐减小的收敛型喷管。把此关系代入式（13.28）中，分析一下压力的变化状态。式（13.28）的左边端面积的变化dA为负，因此右边也应为负。因此，在亚音速M<1条件下的右边括弧项为正，通过喷管的压力变化dp为负，即dp<0。
2.超音速流动
如果是M>1的超音速流动，在式（13.28）的右边项中，因dV和括弧项均为正，故右边为正。因此，左边也应为正，即dA为正，即A2>A1。这表示在超音速流动条件下逐渐增速的喷管形状为，端面积向着气体流动方向逐渐增大的扩散型喷管。把此关系代入式（13.26）中，左边端面积的变化dA为正，因此右边也应为正。因此，在超音速M>1条件下的右边括弧项为负，通过喷管的压力变化dp为负。即，可以看出喷管的作用是通过dp<0获得dV>0。因此，如果要把流体从亚音速增速到超音速，在亚音速领域需要收敛型喷管，在超音速领域需要扩散型喷管，因此采用拉瓦尔喷管。
马赫数M=1时，从式（13.26）和式（13.28）中可知dA=0，即在没有端面积变化的位置上形成，把此部位称为喷管喉。
3.喷管和扩散管
喷管根据喷管出口速度的马赫数分为亚音速、音速、超音速喷管（或拉瓦尔喷管），见表13-5。把所有高温、高压气体膨胀（或减小压力）使用在获得高速上。表中下标0、t、e、a、cr分别表示总（入口）参数、喷管喉、出口、周围、临界状态。如，at为喷管喉的音速，Mt和Me为喷管喉和出口的马赫数。
表13-5 喷管的分类
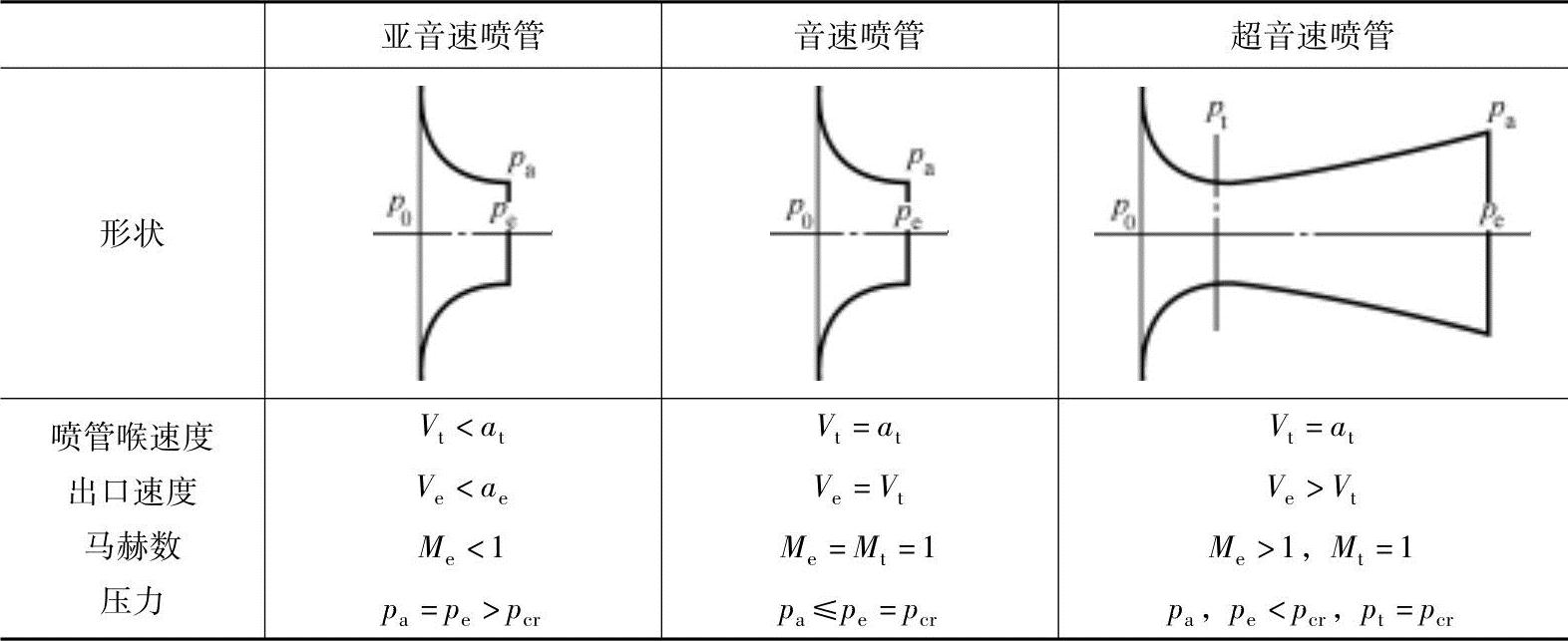
收敛喷管使用在喷管出口压力Pe大于临界压力Pcr的状态，此时出口速度为音速以下，因此还称为亚音速喷管。音速喷管是外部压力（或背压）Pa等于或小于临界压力Pcr时，出口压力Pe等于临界压力Pcr，流出速度等于音速的喷管。
超音速喷管的形状是收敛-扩散型。收敛喷管即使外部压力充分低，喷管出口压力也不会下降到临界压力以下，最大出口速度只能达到音速。如果外部压力Pa充分低，在喷管喉部压力Pt会下降到临界压力Pcr，由此速度达到音速，并在扩散段从临界压力Pcr膨胀到外部压力Pa，因此速度可以获得超音速。火箭推进发动机使用收敛-扩散喷管，以获得马赫数为8以上的排气速度。
扩散管是减小流体速度（dV<0）、增加压力（dp>0）的装置，具有与喷管相反的功能。扩散管使用在压缩器或泵叶片上，喷管所有参数会取相反值，见表13-5。如，通过超音速降低到亚音速以增大压力的收敛-扩散型扩散管，在收敛段把速度从超音速下降到音速，并在扩散段从音速下降到亚音速，以增大压力。
相关文章
- 详细阅读
-
δ2H与δ18O关系探究详细阅读
研究区大气降水线采用全球大气降水线，其公式：4.1.2δ2 H与δ18 O相关关系对地下水δ2 H与δ18 O的监测资料进行统计，分析得到δ2 H＝6.30×δ18 O－6.60‰VSMOW，见图3，R 2为0.62，与LMWL线相比，分馏斜率差别不大，但分馏截距相差近1倍，根据动力分馏原理，说明发生了低湿度的动力（非平衡）分馏［8］。......
2025-09-29
-
内力与截面法：探究杆件强度和刚度的密切关系详细阅读
内力随外力的增大、变形的增大而增大，当内力达到某一限度时，就会引起构件的破坏。内力与杆件的强度、刚度等有着密切的关系。背离截面的轴力称为拉力，指向截面的轴力称为压力。这种假想用一截面将物体截开为两部分，取其中一部分为研究对象，利用平衡条件求解截面内力的方法称为截面法。可见，外力使物体产生内力和变形，不但与外力的大小有关，而且与外力的作用位置及作用方式有关。试求杆内的轴力并作出轴力图。......
2025-09-29
-
边界与载荷条件的关系详细阅读
细观模型的边界条件和损伤断裂模式有比较直接的关系，本节在模型左、右两端考察了三种边界条件对计算结果的影响。在上端采用垂直位移加载控制来模拟单轴拉伸和压缩条件。在下端施加垂直方向约束。计算结果和Arora 等［16］得到的结论一致。图8－16拉伸载荷下三种边界条件的计算结果自由边界；耦合直边；周期性边界图8－17压缩载荷下三种边界条件的计算结果自由边界；耦合直边；周期性边界......
2025-09-29
-
应力与应变的关系探析详细阅读
图2-8 切应力和切应变的方向a）切应力方向 b）切应变方向由上述可知，应力状态与应变状态具有相似性。对于应力与应变的关系，不妨从方向和大小两方面进行叙述。首先讨论应力方向与应变方向之间的关系。对切应力和切应变，可用图2-8来表示。而对于正应力和正应变的方向，就不是这样简单了。......
2025-09-29
-
坐具制造与社会条件的关系详细阅读
第二种解释是，人们还有其他家产。他们认为，家具只是房子的功能延伸。少量高水平的手工艺人为教堂和国家劳动。第四种解释是，中世纪特殊的社会条件是决定坐具的制造和使用的一个重要因素。因为，人们都认为神或者教条可以引导生活，并给人类带来宗教安慰。根据吉恩·法维尔[28]，在沙尔曼的议会里，有伯爵、主教和其他人。矩形管道的流量当量直径按公式计算：图3-28法国国王——沙尔曼的画像(想象)，阿尔布雷希特·丢勒，1512......
2025-09-29
-
冲压加工与板料性能的关系及要求详细阅读
对于绝大多数板料，均可满足这两个要求，但各种材料冲裁后，所得的制件质量与模具的磨损程度相差很大。塑性较好的板料在冲裁后，通常需要进行整修和去毛刺，塑性差的材料或厚板料冲裁时，为了提高板材的塑性，可采取加热方法，如冲裁有机玻璃时一般都需要加热到60℃左右后才冲裁。......
2025-09-29
-
时尚与个体的相互关系详细阅读
西美尔认为时尚外在于个体，时尚向个体展现的易变性是个体自我稳定感的对照，在对照中，个体的自我感意识到自身的相对持续性。随后西美尔对于时尚与个体、时尚与阶级之间关系的论述都是以上面两点为基础和前提的。西美尔认为，作为一种大众行为，时尚可以帮助个体克服羞耻感。在接下来关于时尚与个体关系的论述中，西美尔强调了个体的心理因素对于个人时尚和社会时尚的影响。......
2025-09-29
相关推荐