图2-1 流体静压定义与其作用方向的示意图2.2.2 静压的计算实验表明在静止流场中,液体和气体承受的相对压力,仅与液体或气体的密度和高度有关,而与其他因素无关,这个结论即称为静压理论。根据静压理论计算公式与前面推得 PB=PC的结果,可进一步推得关系式 PB=PA+ρ1ghAB=PC=P0+ρ2ghCD。......
2023-06-29
压缩性流体的流动中,马赫数决定流体的特性。现在用质量热容比κ和马赫数M表示静态参数(T,p,ρ)和总参数(T0,p0,ρ0)之间的关系。
总参数是在对压缩性流动进行说明时表示气体状态的参数,具有如下特征:
①总参数是流体以等熵过程减速到速度为0时的状态参数,是如同静态参数决定流体状态的热力学状态参数。
②正常状态能量方程式是可以把焓和动能之和用总参数进行表示,因此方程式能比想象的更为简单。
③在喷管或扩散管中的流动,因没有功和热量的传递,能量方程式仅存在焓和动能,其和值始终为常数,因此总温和总焓保持不变,即在等熵流动中T01=T02、h01=h02。
④但是,在喷管或扩散管中的流动,即使假设为绝热过程,因存在摩擦损失,总压不会保持不变,即p01≠p02。
1.马赫数与状态参数比
总参数(T0,p0,ρ0)与静态参数(T,p,ρ)之间的关系如同在“12.2.1节中说明的,具有如下关系:

现在用质量热容比κ和马赫数M表示一下上述关系式。在式(13.8)右边第二项V2/(2c0T)中引用质量定压热容c0=κR/(κ-1)、音速a2=κRT和马赫数M(=V/a),可以获得
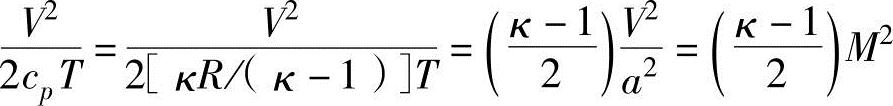
把上式代入式(13.8)中,可以获得温度关系式为

或

利用类似的方法,可以推导出压力和密度相关式:
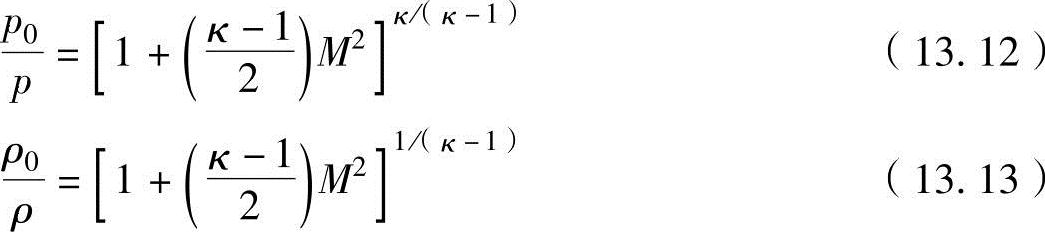
把式(13.11)~式(13.13)称为马赫数关系式,是表示燃烧室的总参数(T0,p0,ρ0)、喷管内任意端面上的静态参数(T,p,ρ)及其位置上马赫数M之间关系的很重要的方程式。对于在喷管出口速度、喷管流通流量式中出现的压力比p/p0,将式(13.12)代入,可以转换为用马赫数表达的方程式。现在用质量热容比κ和马赫数M表示一下任意的压力比p2/p1。对于压力p1可以把式(13.12)用下式表示为
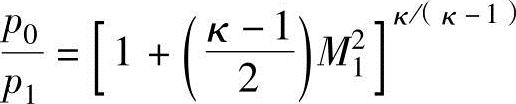
以此,可以获得如下的压力比p2/p1关系式。
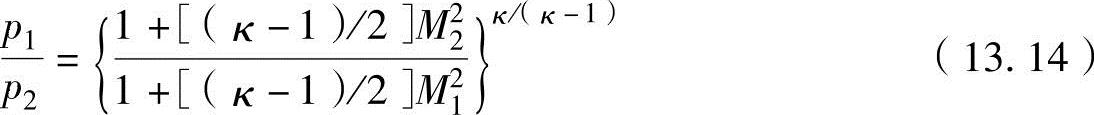
如果是等熵(可逆绝热)流动,如同总焓,总压也保持不变。但如果是非可逆绝热过程,虽然总焓和总温保持不变,但总压不会保持不变。
在等熵流动中,因总焓保持不变,T01=T02,因此利用式(13.11a)可以获得
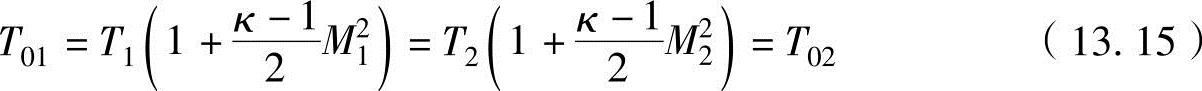
在非可逆绝热过程中,在式(13.14)中代入式(13.12)和式(13.15),可以将总压比表示为

2.马赫数M=1时的状态参数比
在马赫数为1的位置(喷管喉)的流体的状态参数称为临界状态参数。把临界状态参数与总参数之比称为临界比,如图13-11所示显示了在喷管喉部的马赫数为1时的喷管喉的状态参数。在上述式(13.11)~式(13.13)中代入马赫数M=1,可以获得如下临界比公式:
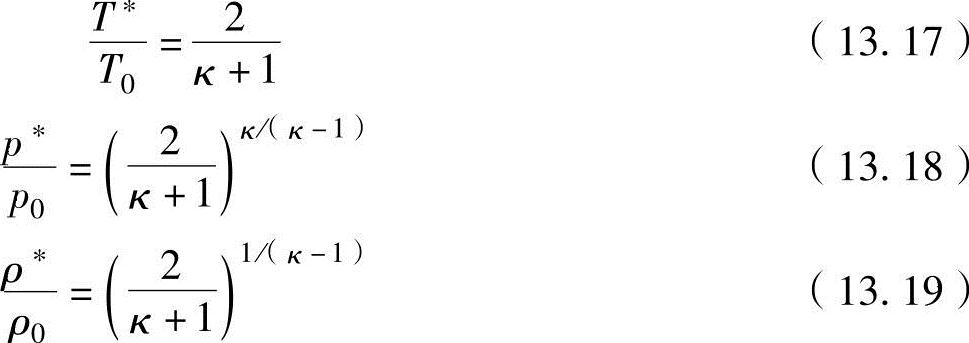
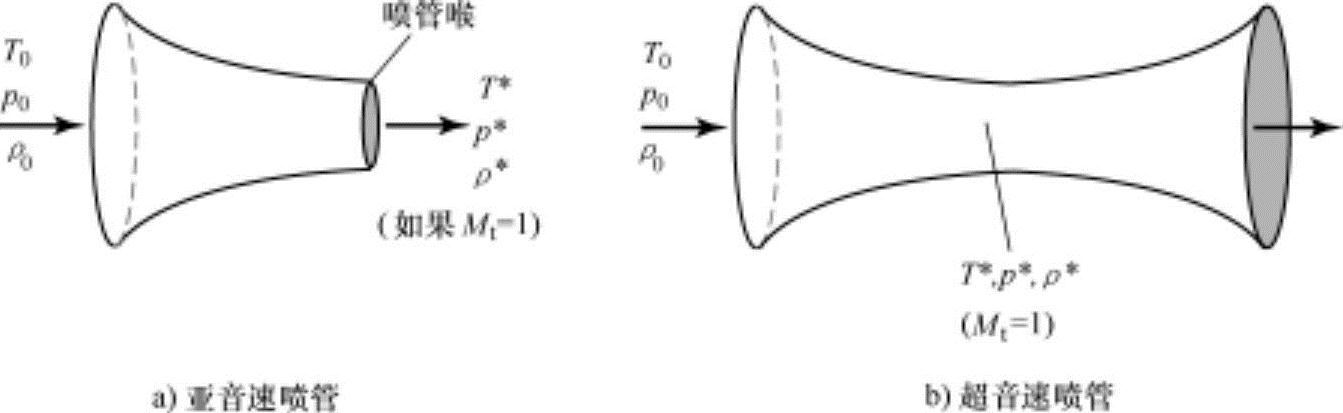
图13-11 喷管喉的状态参数
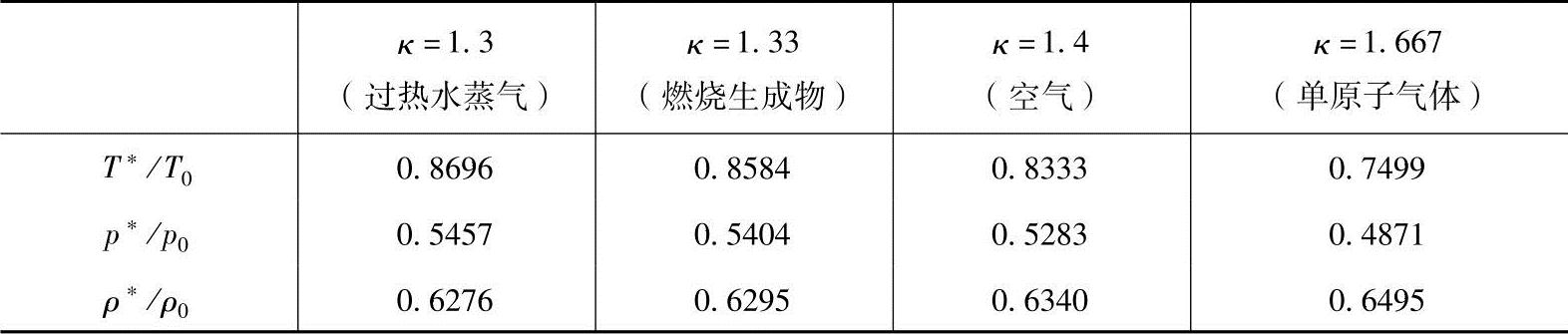
多种质量热容比κ下的临界比见表13-3。
表13-3 等熵流动中多种质量热容比κ下的临界比
在拉瓦尔喷管中,马赫数为1是在喷管喉中发生的。现在用质量热容比κ和马赫数M表示一下M=1的喷管喉状态参数(临界状态参数、以上标*表示)与任意端面上的状态参数之间的关系。
在等熵流动中,因总焓保持不变T0*=T0,根据式(13.11a)可以得到
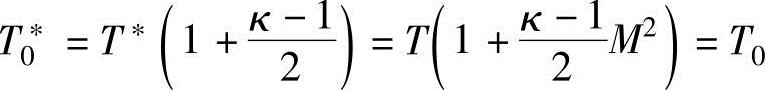
因此,温度比为

根据理想气体的等熵关系式‘T(1/ρ)κ-1=C’,密度比为
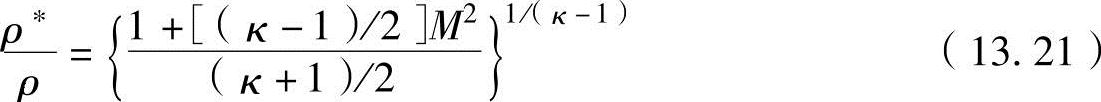
面积比(马赫数为M的部位端面积A与喷管喉部面积A*之比)为
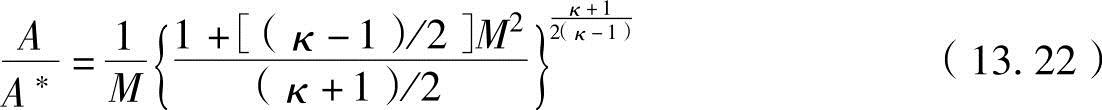
这些公式在亚音速、跨音速及超音速的所有速度范围有效。
3.质量热容比
不仅喷管的流动特性(速度、流量、流量变量等),推力也受到质量热容比κ的影响。理想气体和实际气体(燃烧气体)的质量热容比均为温度的函数。理想气体的质量热容比随温度的上升其变化很缓慢,但实际燃烧气体因在高温条件下发生热裂解,其温度和平均分子量小,以此随温度的改变其质量热容比会发生很大的变化,因此对喷管流动特性和推力有很大的影响。
液体的碳氢化合物燃料与氧气如果以理论混合比进行燃烧,反应生成物为二氧化碳(CO2)和水蒸气(H2O),火焰温度约为3300K。通常,热裂解在低温条件下发生的概率很低,但温度处于1500K以上的高温时,就会很容易发生。以此,像火箭燃烧室处于高温状态下时,一半以上的二氧化碳和水被热裂解,氢气、氧气、一氧化碳、氢氧根离子和氢原子会存在于燃烧气体中,因此平均分子量会变小。喷管燃烧室内燃烧气体的温度达到2000K以上时会发生热裂解,以此燃烧气体的平均分子量会变小,因而喷管喉部的端面积比理想气体时的状态设计为更大。见表13-4所示显示了各种气体质量热容比κ随温度的变化。
表13-4 各种气体质量热容比κ随温度的变化
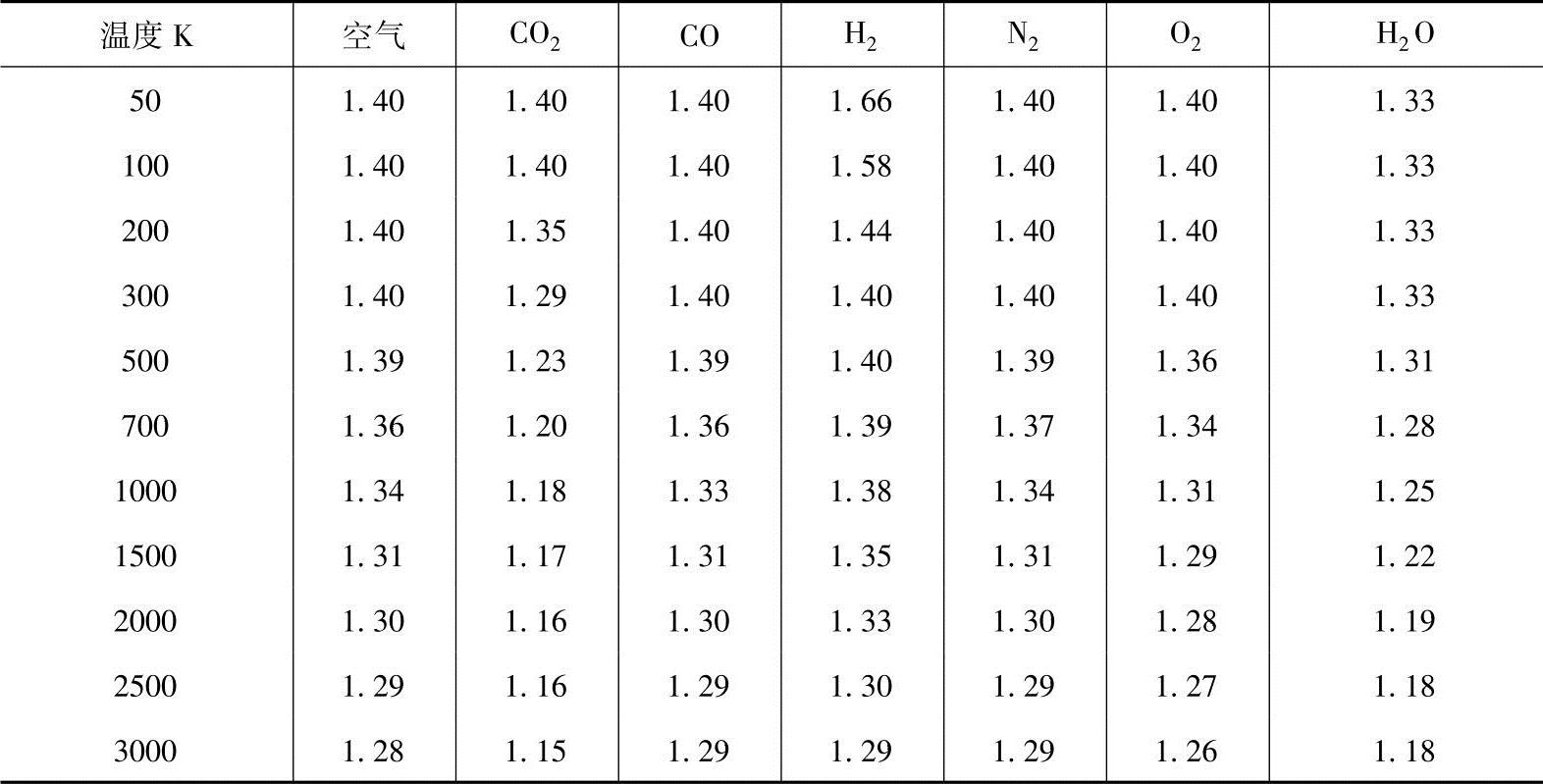
有关内燃机学的文章

图2-1 流体静压定义与其作用方向的示意图2.2.2 静压的计算实验表明在静止流场中,液体和气体承受的相对压力,仅与液体或气体的密度和高度有关,而与其他因素无关,这个结论即称为静压理论。根据静压理论计算公式与前面推得 PB=PC的结果,可进一步推得关系式 PB=PA+ρ1ghAB=PC=P0+ρ2ghCD。......
2023-06-29

具有分散控制、信息集中管理特点的分布式计算机控制系统称为集散控制系统。集散型控制系统的结构通常分三级:第一级为直接过程控制级,第二级为集中操作监视级,第三级为综合信息管理级。典型DCS系统结构图如图5-1-18所示。......
2023-06-26

它是一种能够自动连续、快速、准确地完成信息存储、数值计算、数据处理和过程控制等多种功能的电子机器。所谓硬件子系统系指构成计算机系统的物理元件或物理装置,它包括组成计算机的各部件和外部设备。微机与传统的计算机并无本质区别。它也是由运算器、控制器、存储器和输入/输出接口等部件组成。图1-39列出了计算机硬件系统和软件系统的组成。反之,没有软件或没有完善良好的软件,计算机就无法工作或不能高效率地工作。......
2023-08-26

调洪计算的原理就是根据起始条件,逐时段连续求解水量平衡方程和水库的蓄泄方程,从而求得水库出流过程q—t。若水库设有水电站,且发生洪水时能够运行,则泄洪能力中还应计入水轮机过水流量q电,其值一般可按水轮机过水能力的2/3~4/5计入。综上所述,水库调洪计算的原理,就是由已知的Δt、Q1、Q2、q1、V1、联解式和式,求得q2、V2。......
2023-06-21

FEKO默认采用SEP方法计算介质体,该方法采用三角形网格剖分。2)当对于涂层的相对介电常数与金属线所在的媒质相同时,应用等效理论计算体极化电流。......
2023-10-31

马赫数是指气体的流动速度v与声速c的比值,用符号Ma表示,即马赫数是一个量纲一的参数,常用来衡量气体流动的快慢。马赫数的另一个特征,即反映气体的压缩量。即使压缩性大的气体,如果其流动速度较低或者是静置状态,即气体的马赫数较小,气体的压缩量仍然较小或者为零;反之压缩性小的气体,如果其流动速度较高,即马赫数较大,则气体的压缩量也会比较大。......
2023-08-20

可能最大暴雨就是这两种条件的可能组合,而且降水量最大。3)与历史特大洪水反推的暴雨效率较为接近。图10.2由测站高度化算到1000hPa露点的假绝热图例如某站高度为1000m,露点为22℃,要求换算到1000hPa的露点。......
2023-08-23

定义长度单位单击“Home”菜单中的“Model unit”按钮,在“Model unit”对话框中,选中“Millimetres”单选按钮。磁芯几何尺寸:lx=64;ly=3;lz=8。漆包线与磁芯的间隔:gap=0.1。每个导线向x轴偏移的距离:gapx=0.255。在CADFEKO左侧的树形浏览器中,选中“Media”结点,单击鼠标右键,选择“Metallic medium”选项,创建有限电导率金属。设置磁芯的求解方法为VEP。图5-55 设置磁芯材料的求解方法在“Construct”菜单中,单击“Line”按钮,弹出“Create line”对话框,如图5-56所示,进行如下设置。......
2023-10-31
相关推荐