图9-18为厌氧生物转盘的两种布置形式。厌氧生物转盘的有机负荷率是以单位盘片面积在单位时间内所承受（或去除）的有机物量来表示。厌氧生物转盘的主要缺点是盘片成本较高使整个装置造价很高。根据目前的研究结果表明，影响厌氧生物转盘运行性能的主要因素有水力停留时间、进水水质、有机负荷率及系统的分级等。......
2025-09-29
压缩性流体的特性与应用
【摘要】：图13-10 音波的传播压力波经过压力为p和密度为ρ的气体时，会发生无限小的变化，即dp、dρ、dV。因此，音波经过后的流体状态变化为速度dV、压力p+dp、密度ρ+dρ，如图13-10b所示，引用以固定在波面的坐标，流体以波面为中心右侧以速度a接近，左侧以速度a-dV远离。dh-adV=0 式中，流体速度变化量dV很小，可以忽略其平方项。通常，音波的能量很小，不能改变流体的温度或压力。
1.状态方程式
液体或固体可以看成非压缩性物质，但气体为压缩性物质。气体流动时的压力变化会导致很大的密度变化。流体流动时，表现其状态的变量有速度、压力和温度。此时，为了解释流动状态，需要质量、动量、能量方程式。但是，当增加密度变量时，需要增加一个理想气体状态方程式：
p=ρRT （13.1）
2.音速
液体的流动速度远远小于通过其液体的压力扰动传播速度。与此相反，气体流动时，气体速度与压力扰动传播速度相近或也有可能会超出。在压缩性流动状态下，压力扰动的传播速度是很重要的因素。音波是能用耳朵感觉到的有限大小的压力扰动，这种传播速度即为音速。在此对正常状态流动状态下的音速方程式进行推导。
在静止状态的流体中，如图13-10a所示，对以速度a传播的压力波小的端面进行分析。
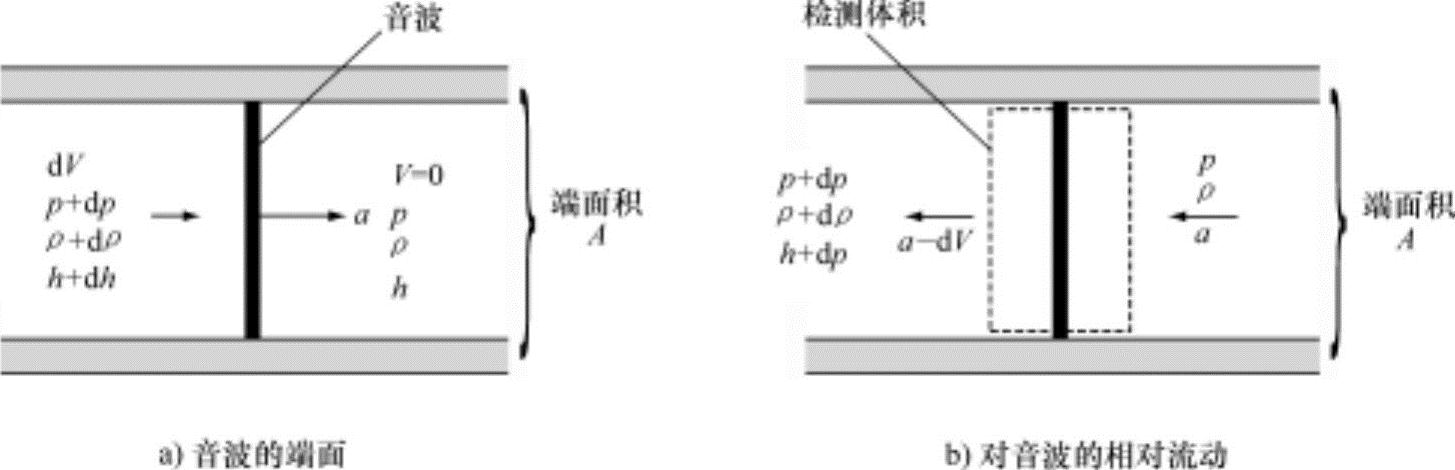
图13-10 音波的传播
压力波经过压力为p和密度为ρ的气体时，会发生无限小的变化，即dp、dρ、dV。因此，音波经过后的流体状态变化为速度dV、压力p+dp、密度ρ+dρ，如图13-10b所示，引用以固定在波面的坐标，流体以波面为中心右侧以速度a接近，左侧以速度a-dV远离。这些变化可以利用质量、动量守恒定律进行解释。
对于包围波面周围的检测体积，分析质量和能量方程式。首先，正常状态的检测体积质量守恒为m1=m2，因此可以表示为
pAa=（ρ+dρ）A（a-dV）
式中，A为检测体积的端面积。因扰乱导致的变化很小，忽略右边的微小高次项，上式可以改写为
adρ-ρdV=0 （13.2）
其次，对检测体积适用能量守恒定律。如果假设检测体积的边界没有热量或功的传递，并且可以忽略势能的变化，则正常状态能量守恒方程可以表示为
(https://www.chuimin.cn)
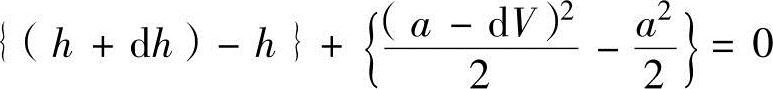
对上式进行分解整理，可以得出下述能量守恒方程。
dh-adV=0 （13.3）
式中，流体速度变化量dV很小，可以忽略其平方项。通常，音波的能量很小，不能改变流体的温度或压力。因此，音波是以等熵过程（可逆绝热过程）进行传播。如果在第2Tds方程式Tds=dh-vdP中应用等熵过程ds=0，因v=1/ρ，因此可以表示为
合并式（13.2）～式（13.4），可以推导出
式中，下标s表示等熵过程。对理想气体的等熵过程状态方程“pvκ=p（1/ρ）κ=C”进行微分，可以得到
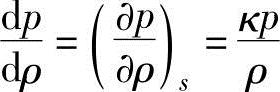
把上述关系代入式（13.5）中，可以获得下述音速计算公式：
从式（13.6）中可知，音速a与绝对温度T的平方根成正比。
空气中传播的音速，因空气质量热容比为κ=1.4，空气的气体常数为R=287J/（kg·K），所以可以表示为
相关文章
- 详细阅读
-
电阻、电感和电容并联电路的特性与应用详细阅读
图1-53所示是一个有趣的试验，先合上开关S1灯泡接通电流IR=1A，IN=1A；再合上开关S2变压器通电，变压器电流IL=0.5A，这时IN=1.1A；最后合上电容开关S3，电容并入电路，电容电流IC=1.25A，可这时总电流IN=1.25A。当RL支路中的IL＞IC时，总负载为感性；当RL支路中的IL＜IC时，总负载为容性；当RL支路中的IL=IC时，则总电流和电压同相，这时电路的状态为并联谐振或称为电流谐振。......
2025-09-29
-
稀土磷钒钛耐磨铸铁的特性分析与应用详细阅读
表5-30 稀土磷钒钛耐磨铸铁MTRPVTi20牌号化学成分要求 2.熔炼控制要点1）炉料组成。钒钛生铁：100；Si452.7～3.0；FeP21.6～1.8；Mn3 1.6～1.8。用列表表示如下：2）钒钛生铁中元素烧损率：V15%～20%，Ti40%～50%。3）炉前用稀土硅铁合金195023进行孕育处理。4）加入100%钒钛生铁时，块度大，注意采用预热送风、大风量和适当增加焦耗等措施，保证较高的出铁温度。......
2025-09-29
-
双相不锈钢的特性及应用详细阅读
表7-2列出奥氏体、双相不锈钢在不同介质中的耐应力腐蚀性能的比较。试验结果表明，双相不锈钢的耐应力腐蚀性能远高于奥氏体不锈钢。双相不锈钢由于晶粒细小，屈服强度很高，其冷成形性能低于中铬铁素体不锈钢和奥氏体不锈钢。图7-2 相比例对双相不锈钢高温下塑性的影响......
2025-09-29
-
湍流模型及其应用于流体数值模拟的研究详细阅读
湍流的重要特点是物理量的脉动，目前描述湍流流动的数值模拟方法主要包括直接数值模拟、大涡模拟和分离涡模拟等。分离涡模拟方法是将大涡模拟和雷诺平均方法结合，在壁面处采用分离涡模拟方法，在湍流的核心区域采用大涡模拟方法。模型考虑了网格的各向异性，且调整亚网格长度尺度来实现RANS向LES的过渡。除此之外，为解决近壁雷诺应力估计不足的问题，IDDES模型中增加新项fe。......
2025-09-29
-
聚乙烯（PE）及其特性和应用详细阅读
高压聚乙烯高分子带有许多支链，因而相对分子质量较小，结晶度和密度较低，且具有较好的柔软性、耐冲击及透明性好。中压聚合所得到的聚乙烯为中密度聚乙烯。聚乙烯有高度的耐水性，长期与水接触其性能可保持不变。一般高压聚乙烯的使用温度在80℃左右，低压聚乙烯为100℃左右。......
2025-09-29
-
连续激光切割的特性及应用详细阅读
高的切割速度1200W的CO2激光切割2mm厚低碳钢板的切割速度达到0.1m/s，切割5mm厚有机玻璃的切割速度0.2mm/s；激光切割钢板生产率达到冲模下料的30%左右。试验设备和材料 其试验设备采用波长为10.6μm、功率为4kW的快速轴流CO2激光器，光束聚焦使用125mm的透镜。......
2025-09-29
-
PARLED灯的特性及应用场景详细阅读
PAR灯是采用大功率LED作为光源并且需要专用的PAR灯透镜的灯具。包括PAR16、PAR20、PAR30、PAR38、PAR64等。常见的有PAR30、PAR38，功率有5×1W、7×1W、12×1W。无论PAR30还是PAR38，其使用的LED透镜的外形规格都是相同的，最大直径一般为19.8mm左右，卡口（台阶）直径为17.8mm左右。3）PAR灯透镜的安装，除了利用灯杯前部面板卡VI固定外，透镜的小内口与LED的接触方式也有两种。2）PAR灯透镜以38°应用得最多。......
2025-09-29
相关推荐