根据叠加原理，式可写成以下形式：图14-12位移条件式就是为求解多余未知力X1和X2所需要建立的力法方程。对于高次超静定问题，其力法方程也可类似推出。当原结构在去掉多余约束处的已知位移为零时，其力法方程为方程中的系数称为柔度系数，位于主对角线上的系数δii称为主系数，在主对角线两侧的系数δij称为副系数，Δ1P称为自由项。由于基本体系是静定的，所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。......
2025-09-29
如何计算反动度？——涡轮反动度计算方法
【摘要】：全级的焓变化通过式和式推导，可得h01-h03=h02-h03=U=U 工作叶片中以与工作叶片一起旋转的观察者角度上进行观察，因没有动力传递，可以视为相对总焓保持不变，即h02，rel=h03，rel，有此外，轴向速度一定时，通过速度三角形进行分析，可得W23-W22=W2w3-W2w2 把这些关系式代入式中并推导，可得反动度公式为把式与速度关系式合并，还可以将反动度表示为反动度ξ为0的条件从式中可以看出，是在相对流动角度β2与β3相同时的状态。图12-35 反动式涡轮的速度三角形和叶片形状
涡轮反动度ξ是工作叶片中燃烧气体膨胀程度的尺度，定义为涡轮全级（导向叶片+工作叶片）中焓减小量对工作叶片中焓减小量之比。
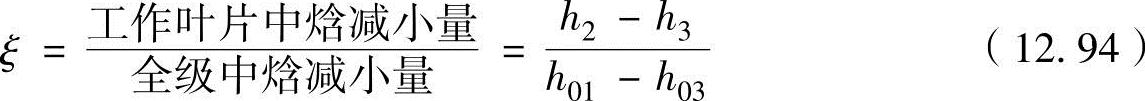
在运行温度范围内，质量定压热容cp的变化量小，用焓的减小比表示温度的减小比。在非压缩性等熵流动中，焓的变化比等于压力的变化比。因此，反动度还表示涡轮全级中压力减小量对工作叶片中压力减小量之比。
反动度为ξ=0的涡轮，焓减小量（或压力降）全部在导向叶片中发生，在工作叶片中没有任何压力降，仅消耗所具有的动能获得涡轮功，这种涡轮称为冲动式涡轮。合理设计工作叶片的形状，可以使工质流体在通过工作叶片时也发生压力降，即发生膨胀，从而获得膨胀时的反作用功，这种涡轮被称为反动式涡轮。反动度为ξ=0.5时，说明导流叶片与工作叶片中的焓减小量相同，这表示冲动作用和反动作用各占一半，把这称为反动式涡轮有点怪怪的，这是因为轴流式涡轮中发生反动作用仅在ξ=0.5时产生。通常，轴流式涡轮使用的反动度ξ的值为0和0.5。现在对涡轮叶片的形状进行分析。
全级的焓变化通过式（12.88）和式（12.83）推导，可得
h01-h03=h02-h03=U（Vw2+Vw3）=U（Ww2+Ww3） （12.95）
工作叶片中以与工作叶片一起旋转的观察者角度上进行观察，因没有动力传递，可以视为相对总焓保持不变，即h02，rel=h03，rel，有
此外，轴向速度一定时，通过速度三角形进行分析，可得
W23-W22=W2w3-W2w2 （12.97）
把这些关系式代入式（12.94）中并推导，可得反动度公式为(https://www.chuimin.cn)
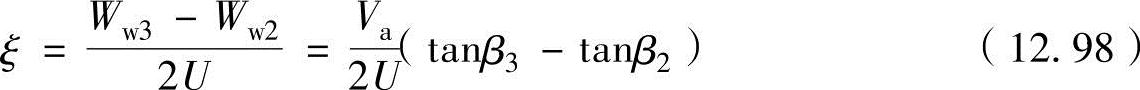
把式（12.98）与速度关系式（12.83）合并，还可以将反动度表示为
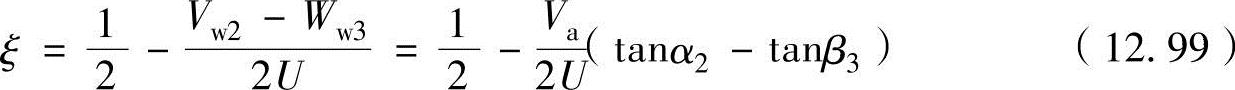
反动度ξ为0的条件（冲动式涡轮）从式（12.98）中可以看出，是在相对流动角度β2与β3相同时的状态。在反动度为0的条件下，轴向速度保持不变的状态速度三角形和叶片形状如图12-34所示。对叶片形状进行观察，工作叶片的形状上前后的速度方向相反大小相等，因此在工作叶片上不发生膨胀。与此相反，在导向叶片上速度大幅度增加，发生很大的膨胀。因此，所有的膨胀仅在导向叶片上发生。
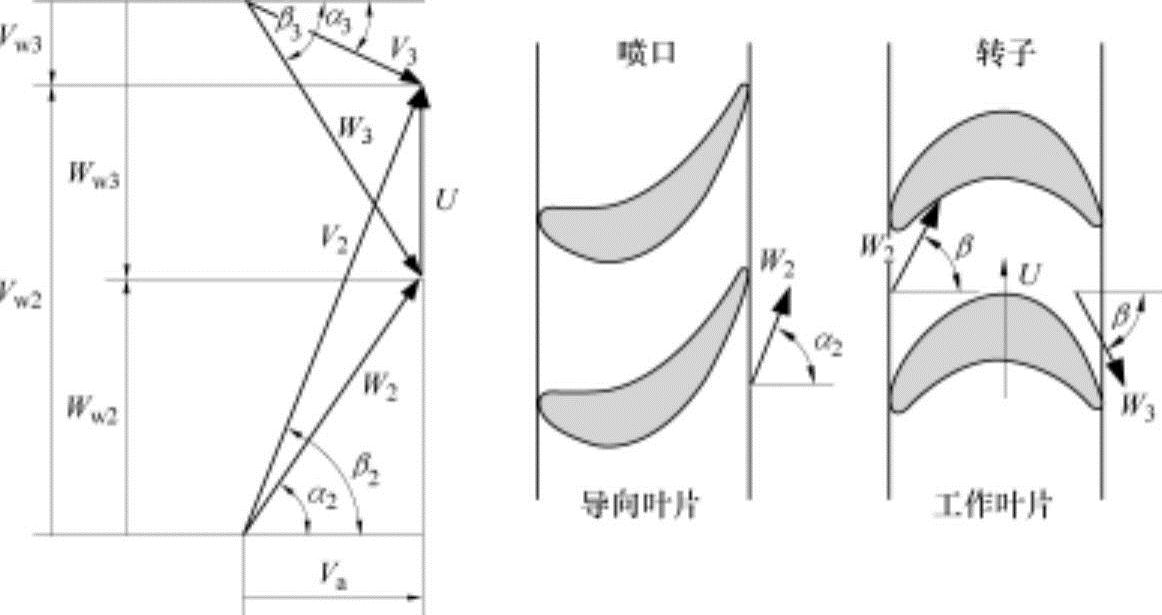
图12-34 冲动式涡轮的速度三角形和叶片形状
反动度ξ为0.5的条件（反动式涡轮）从式（12.99）中可以看出，是在导向叶片的出口绝对速度流动角度α2与工作叶片出口相对速度流动角度β3相同时的状态，如图12-35所示。反动式涡轮中，因具有β2=α3，C2=V3和C3=V2的关系，工作叶片与导向叶片的形状相同。因此，工作叶片与导向叶片中发生的膨胀程度相同，从而使焓和温度的减小程度相同，即工作叶片与导向叶片中膨胀和压力降程度相同。如果反动度小于0.5，则说明导向叶片中的压力降更大。
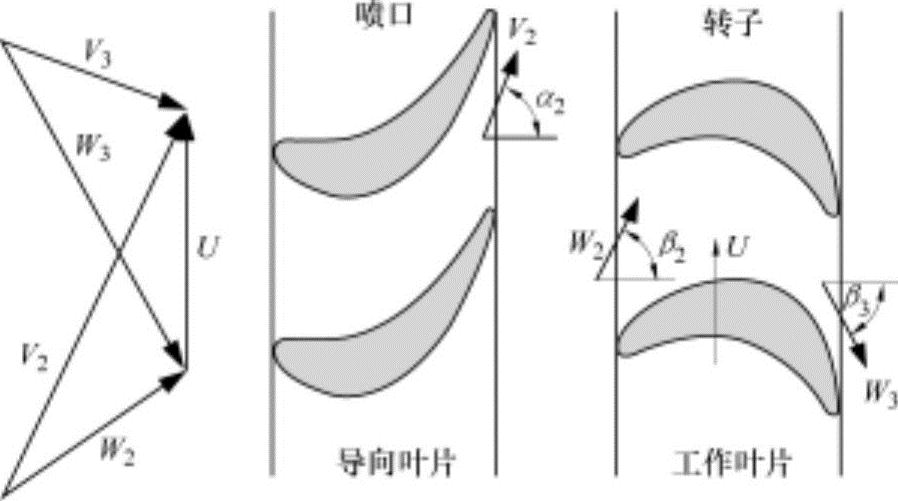
图12-35 反动式涡轮的速度三角形和叶片形状
相关文章
- 详细阅读
-
压杆柔度与临界应力的欧拉公式计算方法详细阅读
于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式，式中λ称为压杆的柔度。从式（9-3）还可以看出，压杆的柔度值越大，则其临界应力越小，压杆就越容易失稳。因此，欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP，即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值，则故欧拉公式的适用范围为上式表明，当压杆的柔度不小于λP时，才可以应用欧拉公式计算临界力或临界应力。......
2025-09-29
-
剪切的常见计算方法详细阅读
剪切试验试件的受力情况应模拟零件的实际工作情况进行。若以A 表示销钉横截面面积，则应力为τ 与剪切面相切，故为切应力。以上计算是以假设“切应力在剪切面上均匀分布”为基础的，实际上它只是剪切面内的一个“平均切应力”，所以也称为名义切应力。当F 达到Fb 时的切应力称剪切极限应力，记为τb。对于图5-8 所示的剪切试验，剪切极限应力为用τb 除以安全系数n，即得到许用切应力这样，剪切计算的强度条件可表示为......
2025-09-29
-
如何选择表面粗糙度？详细阅读
表面粗糙度的评定参数值国家标准都已标准化。一般来说，选择的表面粗糙度参数值越小，零件的使用性能越好。4）表面粗糙度参数值应与尺寸公差及几何公差协调一致。5）对密封性、耐蚀性要求高，以及外表要求美观的表面，其表面粗糙度参数值应小。......
2025-09-29
-
如何测量表面粗糙度？详细阅读
对表面粗糙度的评定分为定性评定和定量评定两种。定量评定是指借助各种检测仪器，准确地测出被测表面粗糙度参数值。比较法简单易用，多用于生产现场判断零件的表面粗糙度，比较法判断的准确程度和检验人员的技术熟练程度有关。2）光切法光切法是利用光切原理来测量表面粗糙度的一种测量方法。......
2025-09-29
-
表面粗糙度简介详细阅读
表面粗糙度影响配合性质的稳定性。此外，表面粗糙度对零件的外观、测量精度也有一定的影响。为了获得较小的表面粗糙度，零件要经过复杂的加工，会引起加工成本的急剧增加。因此，表面粗糙度的参数值在设计过程中应该合理选择。图5-2表面粗糙度的概念......
2025-09-29
-
关联规则计算方法详解详细阅读
，xm}是一组称为项的元素的集合，集合XI称为项集。关联规则是一个表达式X→Y，其中X和Y是项集且不相交，即X，YI，其中N∩Y＝。为了生成频繁且高置信度的关联规则，首先要枚举所有的频繁项及其支持度。给定数据集D和用户自定义的支持度阈值minsup；其次，给定频繁项集的集合F和最小置信度minconf，关联规则挖掘的任务是找出所有频繁且置信度高的规则。......
2025-09-29
-
CFX的设置与计算方法优化详细阅读
注意：前面的3.2节中已详细讲述了CFX设置，且本书主要是针对泵设置的。故本节以及后面提及CFX设置的章节，对于设置的描述不再很详细。图4.1-33 基本设置图4.1-34 流体模型设置5）其他水体也按照上述1）～4）步骤设置，不同的是基本设置中的“Domain Motion”设置为静止“Stationary”的，其他默认，如图4.1-35所示。其他栏均保持默认设置。......
2025-09-29
相关推荐