图11-24 接刀轴磨削3.磨削实例工件如图11-24所示，磨削工序尺寸图11-25 螺纹磨床主轴见表11-7，要求外圆无明显接刀痕迹。表11-7 接刀轴磨削工序尺寸4.容易产生的问题及注意事项1)磨削前应检查中心孔的质量，并保护好中心孔，工件磨出后测量圆柱度误差应小于0.003mm，以免接刀时产生偏痕。......
2023-06-28
如何优化汽车引擎的T-s线图与增压比？
【摘要】：即，因V3T2。在此T-s线图中，对工作叶片和导流叶片的损失进行分析。但因实际过程为非可逆过程，因此不能获得与等熵过程相同的压力增大。把式对增压比Rs进行推导，可以改写为式中，适用一级压缩器中的总温增加量ΔT0s和速度关系式，可以将增压比表示为从上式中可以看出，如果效率ηs不变，为了获得大的增压比，必须增大工作叶片的转速U和圆周方向的绝对速度变化量ΔVw。
压缩器的导流叶片上没有输入动力，可以考虑为等熵过程，根据能量守恒定律总温T0和总焓h0保持不变。因此，如图12-18a所示，以下标2、3分别表示导流叶片进口和出口时，能量守恒式为
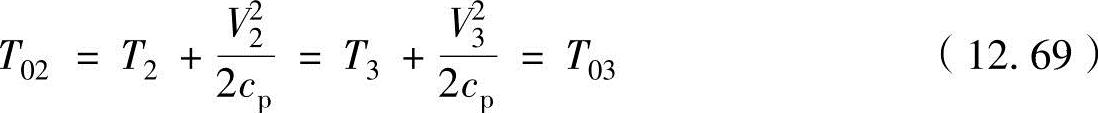
参考图12-18b所示的速度三角形，在导流叶片中绝对速度会降低，温度会增加。即，因V3<V2，有T3>T2。相反，在工作叶片中与获得的动力成正比，总温会增大，即T02>T01。但是，当以与工作叶片一起旋转的观察者角度上观察工作叶片时，等于没有输入动力，因此相对总温T0，rel（以相对速度W计算的总温）不变，如下式表示。
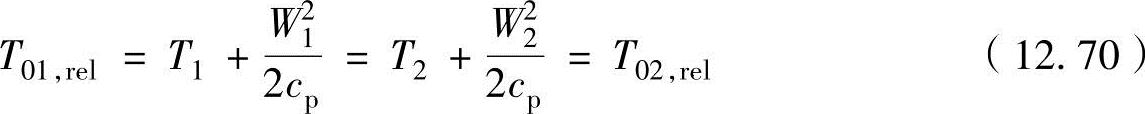
在工作叶片上相对速度减小，温度上升。即因W2<W1，有T2>T1。考虑此关系，在轴流式一级压缩器的状态变化如图12-19所示。在此T-s线图中，对工作叶片和导流叶片的损失进行分析。在工作叶片经过期间，总温与输入动力成正比增加，但如式（12.78）所示，相对总温保持不变，因此温度T以与相对速度减小量成比例的速度增加。如此，在工作叶片中温度和总温增加，同时压力和总压均要增大。但因实际过程为非可逆过程，因此不能获得与等熵过程相同的压力增大。
一级压缩器的等熵效率ηs为
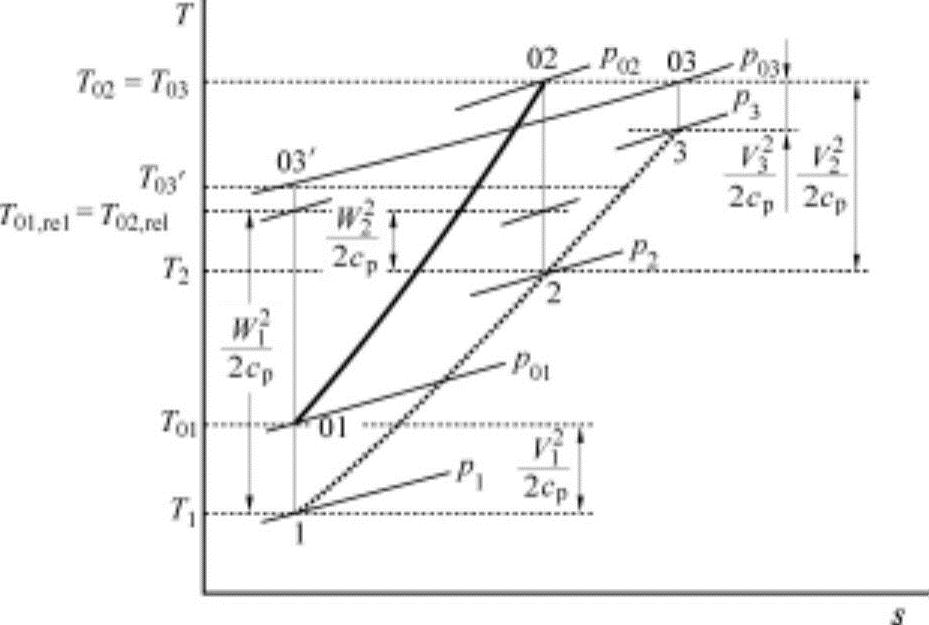
图12-19 一级压缩器的T-s线图
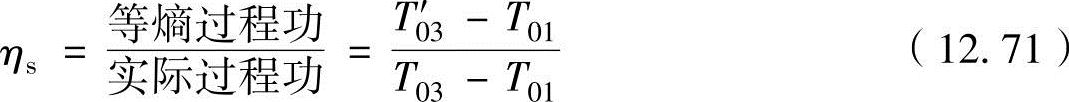
利用理想气体的等熵状态式T（1-κ）/κp=常数，式（12.71）可以改写为
式（12.72）所示的一级压缩器的效率可以作为以相同的温度比能获得多少增压比的尺度。
把式（12.72）对增压比Rs（=p03/p01）进行推导，可以改写为
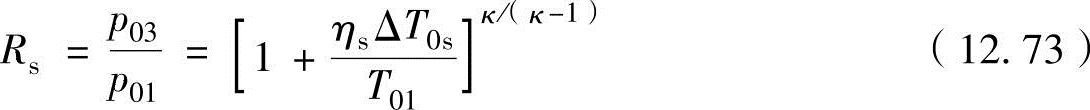
式中，适用一级压缩器中的总温增加量ΔT0s（=T03-T01）和速度关系式（12.68），可以将增压比表示为
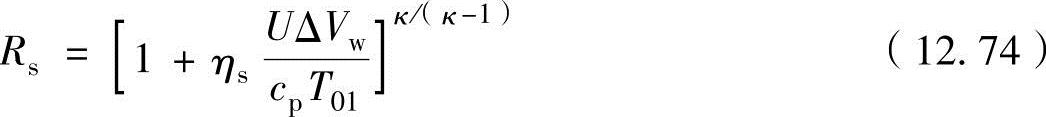
从上式中可以看出，如果效率ηs不变，为了获得大的增压比，必须增大工作叶片的转速U和圆周方向的绝对速度变化量ΔVw。在此考虑速度三角形，可以获得关系式：
U=Vw1-Ww1=Vw2-Ww2 （12.75）
因此，有
ΔVw=Vw2-Vw1=Ww2-Ww1=Va（tanα2-tanα1） （12.76）
从式（12.76）可以看出，圆周方向绝对速度变化量与轴向速度和工作叶片中的流动角度变化量有很大的关系。因此，为了增加压缩器各级的增压比，必须增大下述要素：
①工作叶片的转速U。
②轴向绝对速度Va。
③工作叶片的流动角度的转换（α2-α1）。
有关内燃机学的文章
- 详细阅读
-
如何优化汽车固定箍圈的制造工艺？详细阅读
排样图：如图10-23b所示。说明：1.工艺分析如图10-23a所示为某汽车固定箍圈，该制件形状复杂，是一典型的圆筒卷圆件，以前曾有类似的制件，按照传统工艺预弯，卷圆成形后出现了较大的回弹，回弹后圆筒件直径一般增大5～8mm，而且圆筒件有明显的椭圆化倾向，虽经反复调整，修研模具，但效果一直不理想，难以冲压出合格的制件。......
2023-06-26
-
如何绘制合理的接线图？详细阅读
接线图绘制的方法有多种，应根据产品的应用场合不同，线路的复杂程度不同，合理选择接线图的绘制方法。5）编制接线表，完成全图。图3-7 直接式接线图基线式接线图将图上各端点引出的导线，束成一条称为“基线”的直线上，这种接线方式的图，叫做基线图。基线一般画在各元器件的中间。用基线式接线图的产品，其内部排列整齐，固定方便、牢固，防振。干线图的优点同于基线图。能近似反映出设备内部电路的连线情况，比基线图直观易读。......
2023-06-28
-
如何绘制端子接线图？详细阅读
图11-45 绘制端子接线图实例图11-45 绘制端子接线图实例在“快速访问”工具栏中单击“新建”按钮，弹出“选择样板”对话框，从随书光盘的“图形样板”文件夹中选择“ZJDQ_X.dwt”图形文件，单击“打开”按钮。如果要绘制带有远端标记的端子接线图，远端标记注写在连接线的中断处，如图11-54所示。有兴趣的读者可以分别练习如何绘制这两个端子接线图。保存文件，保存的文件名为“端子接线图.dwg”。......
2023-06-20
-
如何优化混合比以实现最大输出功率？详细阅读
输出功率最大时的空燃比称为最大输出功率空燃比，其值约为12.5。在节气门全开运行时，空燃比A/F=13附近的水平线从低转速到最高转速的范围内也因需要最大输出功率，因此处在浓混合比状态。如上所述，电控发动机可以根据负荷的要求调整混合比，在废气排放法规下配备了三元催化转化器，在除了冷起动、急加速等状态外的所有运行条件下，在接近空气过量系数（λ=1）的理论空燃比附近运行。......
2023-06-28
-
搜索引擎的优化检索功能详细阅读
搜索引擎的一个核心功能是其检索功能。从现有的搜索引擎来看，它们都已具备了诸如布尔检索、词组检索、截词检索、字段检索、限制检索和位置检索等基本检索功能。网络信息检索工具一般以符号来代替布尔关系，形象地表达布尔检索的功能。假如检索工具支持模糊检索，上述提问能够达到预期检索效果。在此意义上，概念检索实现了受控检索语言的一部分功用，即考虑到了同义词、广义词和狭义词的使用。......
2023-07-02
-
聚焦搜索引擎算法的优化详细阅读
Lingo算法是基于奇异值分解的索引结果聚类算法。系统使用Lingo算法的主要目的是提高聚类标签的质量。2)Rough K-means算法的选择取决于数据的类型、聚类的目的和应用。每个簇中对象的平均值称为该簇的聚点，也就是中心。两个簇的相似度是根据两个聚点计算出来的。图2-21K-means算法流程图K-Means算法是最基本的非层次聚类算法，它假设各个类都呈现球状且类的大小几乎相等。另外用到的算法还有STC后缀树聚类算法，HAOG和FuzzyAnts，比较有难度，在此不做介绍。......
2023-07-02
-
如何改善涡轮增压器效率？详细阅读
图6-54 空气充量系数、有效压力、热效率之间的关系图6-55 通过可变几何涡轮增压器提高燃油效率双级涡轮增压器 目前，根据不同运行领域选择使用双级涡轮增压器的结构正在开发应用中。因此，作为更加积极的方法，把涡轮增压器设计为双级涡轮增压器。双级涡轮增压器不仅提高动力性能，还能提高效率，从而获得降低有害气体生成量的增值效果。但是这需要能有效控制双级涡轮增压器的最佳控制逻辑。......
2023-06-28
相关推荐