此转子在受到扰动后，就要以线为平衡位置发生自由振动。就是说转子在不平衡离心力这一激振力的作用下，发生同频率的振动，振幅与激振力大小、转子的质量、刚度及转速等有关。上述各种阻尼中，对转子振动影响最大，因而也是对转子稳定运转影响最大的是轴承油膜阻尼。在有阻尼的情况下，单圆盘转子的不平衡振动，可以抽象为见图7-3的单圆盘转子振动力学模型。......
2023-08-20
曲轴振动及其影响分析
【摘要】：发动机发生的旋转力（转矩）随曲轴角度发生很大的变化，曲轴不断地进行被扭曲再恢复原状态的弹性变形运动，因此在曲轴周围发生强制扭转振动。此时的发动机转速称为扭转振动的临界转速。③在曲轴系统的耦合器内放入橡胶等弹性体，以改变振动系统。图10-14 防扭转振动的扭振阻尼器
发动机发生的旋转力（转矩）随曲轴角度发生很大的变化，曲轴不断地进行被扭曲再恢复原状态的弹性变形运动，因此在曲轴周围发生强制扭转振动。此时，如果扭转振动频率（振动数、发动机的爆发次数）与曲轴系统（曲轴、飞轮、离合器和连接体）的固有振动频率相同，曲轴会发生共振，振幅变化很大，则曲轴因疲劳应力会被破坏。此时的发动机转速称为扭转振动的临界转速。
扭转振动是在曲轴系统中没有考虑过的应力，不仅给曲轴系统，还给曲轴箱、连杆、动气门机构等部件也带来过大的应力。因此，为了发挥稳定的最大输出功率，应分析把握发动机的振动特性，并采取相应的补救措施。
1.扭转振动的基础方程
图10-12所示为轴的一端固定，另外一端固定有质量惯性转矩圆盘的扭转振动模型。当圆盘扭转某一角度θ时，因轴为弹性体产生恢复到初始状态的旋转力（与θ成正比）-kθ，此现象反复成为振动。如果此系统中作用有周期性的外力T（=T0Sinωt），则扭转振动相关普通运动方程为
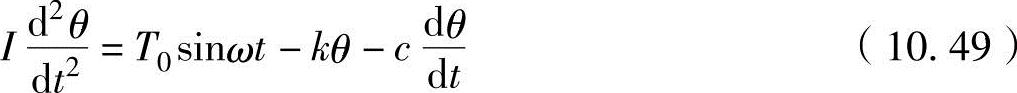
式中，I为惯性转矩；c为黏性系数；k为扭转相关弹性系数；T0Sinωt为强制振动力（外力）；t为时间。假设没有外力，两边以惯性转矩I相除，并设定c/I=2n、k/I=p2，则可以推导出
上述微分方程的解为
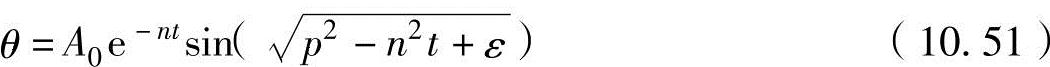
式中，A0为t=0时的扭转振幅；l/n为衰变率；A0、ε分别为初始条件常数。式（10.51）显示为振幅逐步衰减的正弦波振动类型，如图10-13所示。此振动的角速度为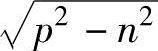
。
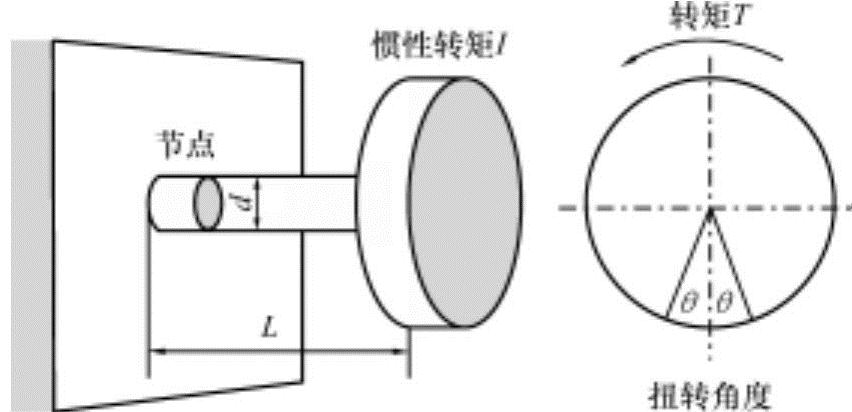
图10-12 旋转系的扭转振动模型
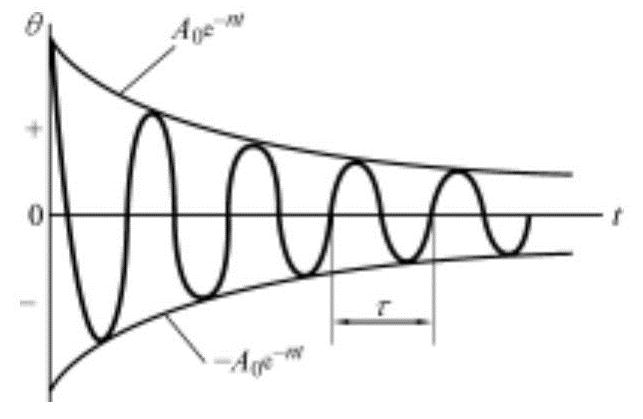
图10-13 衰减自由振动
振动周期τ（S/循环）和固有振动频率f（循环/S）的计算式为
①没有衰减的自由振动（c=0，n=0）时
②有衰减的自由振动时
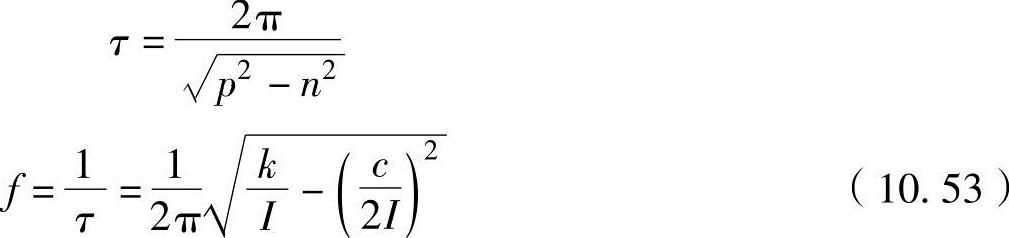
从式（10.53）可以看出，有衰减时的周期比没有衰减时的周期稍微长。
2.防扭转振动方法
因多气缸发动机的点火间隔相同，在曲轴旋转1周中爆发次数相同或其整数倍的次数上出现临界转速，把此称为主临界转速，除此之外的次数称为亚临界转速。通常，主临界转速时角振幅发生较大变化，如果此转速处于发动机常用转速范围内，会导致曲轴系统被破坏或在多处发出异常噪声。
常用转速范围较窄的发动机可以设计为避开发生共振的临界转速范围，但常用转速范围较宽的发动机，如果曲轴系统的固有振动频率在使用转速范围内，则提高固有振动频率等的措施如下：
①加大曲轴刚性。
②相反地降低刚性，快速通过与固有振动频率相同的发动机转速领域。
③在曲轴系统的耦合器内放入橡胶等弹性体，以改变振动系统。
④在曲轴系统上配备黏性阻尼器或摩擦阻尼器等，把振动能量转换为热能，以防止发生振动。
⑤在曲轴系统上附加特殊的振动系，如动态阻尼器，通过共振时产生的反力或反力矩，来消除振动力或振动力矩。
⑥如果固有振动频率高，则其应力大时，应采用扭振阻尼器。
通常，直列6气缸发动机的曲轴比相同容积的直列4气缸发动机曲轴更容易发生扭转振动。这是因为曲轴的长度越大，其扭转刚性越小。图10-14所示为防扭转振动用扭振阻尼器的例子，是与曲轴带轮整体化的橡胶阻尼器和硅油阻尼器。
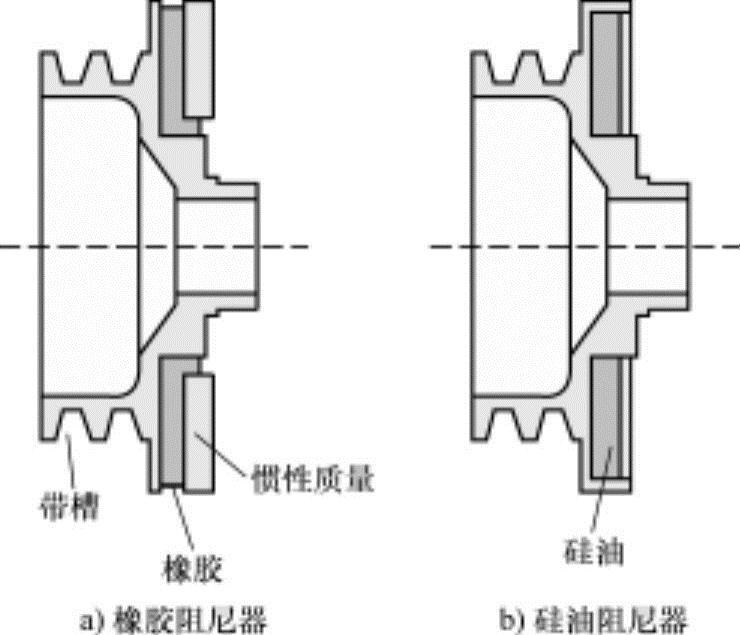
图10-14 防扭转振动的扭振阻尼器
有关内燃机学的文章
- 详细阅读
-
曲轴旋转力分析详细阅读
首先对展开式所需的三角函数关系式进行分析：如图10-4所示，曲轴销旋转力的关系式为此切线力Ft与曲轴半径r的乘积Ftr为相对于曲轴角θ的旋转力。这是因为燃烧气体力Fg在做功过程中推动曲轴旋转，反过来在压缩过程中施加压缩力，另外惯性力Fi在曲轴每旋转1周期间瞬间旋转角速度不一致。图10-10所示为6气缸发动机的转矩曲线和单气缸发动机的转矩曲线。转矩的变化通过配备旋转运动质量较大的飞轮可以进一步平稳化。......
2023-06-28
-
振动诊断技术及其应用现状详细阅读
由于振动诊断具有诊断结果准确可靠和便于实时诊断等诸多优点，因而它成为应用最广泛、最普遍的诊断技术之一。特别是近年来，随着振动信号采集、传输以及分析用仪器技术性能的提高，更进一步地促进了振动诊断技术在机械故障诊断中的应用。ψ称为简谐振动的相位，是时间t的函数，单位为rad。表5.2根据振动后果选择振动监测参数测量参数选择的另一个问题是振动信号统计特征量的选用。......
2023-06-22
-
VFTO特性分析及其影响因素详细阅读
VFTO的幅值与隔离开关触头间电弧重燃电压大小有关，也与被开断的母线上的残余电荷产生的电压值有关，具有随机特性。开断长母线时引起的VFTO幅值较低。而断路器断口间均压电容的增大可造成GIS内部VFTO的幅值有所降低，主变处的过电压幅值也有降低趋势。相比之下，SF6母线波阻抗的大小对VFTO影响略小。GIS外部，高压电缆长度对VFTO幅值影响最大。尤其对GIS内部的暂态过程而言，对VFTO影响更不明显。......
2023-07-02
-
窗函数的作用及其影响分析详细阅读
2）通带内增加了波动，在ωc-2π/N处出现过冲为0.089的最大正峰。3）阻带内产生了余振，在ωc+2π/N处出现过冲为-0.090的最大负峰。图3-2是当N分别取4、8、16、32时Hdg（ω）和Hg（ω）的波纹变化。图3-3中，当阶数N由24增大到216时，由于旁瓣数量的增加致主瓣能量占比逐渐降低，最大正峰的过冲程度也随着N的增大而逐渐减小，但阶数增大至210以后，过冲程度基本没有再改善。......
2023-06-23
-
发明者教育程度及其影响分析详细阅读
罗斯曼对于发明者教育背景进行调查研究，客观分析了发明者所接受的教育程度与其发明活动之间的关联[11]。为了解答这些问题，罗斯曼针对452位专利权人的教育背景进行统计分析，这452位发明者分别在1927、1928或者1929年获得四项以上专利权，他们一直持续从事发明活动，人均专利是46．3项，可以作为发明者的样本来进行研究，其统计数据也相对具有合理性。......
2023-11-27
-
金属焊接性及其影响因素分析详细阅读
工艺焊接性是通过金属材料焊接性试验来实现，而使用焊接性则通过焊接工艺评定来实现。例如，钛金属在焊接过程中，400℃以上的区域都要用惰性气体保护，否则，该温度区域的钛金属氧化，力学性能变差，因此，焊接钛金属比焊接低碳钢要难得多。如钛金属用真空电子束焊接方法很容易获得高质量的焊缝，而用氩弧焊方法焊接，需要设计一套保护装置，在焊接过程中，将400℃以上的区域进行氩气保护，防止钛金属的氧化。......
2023-06-15
-
求解1.5.2固有振动分析详细阅读
本节将说明完成前处理后的计算求解方法。图1-137 计算的选项3）单击“OK”按钮，所估计的数值就会显示。图1-140 固有振动计算的算法3）“Number of Modes”选项定义要计算的模态个数，其默认值为10。Lanczos法较适合大于10万自由度且需要计算高阶模态的情况，还可作频率漂移。图1-141 固有振动计算的Lanczos算法图1-142 固有振动的Lanczos算法的设定......
2023-06-21
相关推荐