全熔透对接焊缝接头静载强度计算时，焊缝的计算长度取实际长度，计算厚度取对接接头中连接板中较薄部分的厚度，也可取T形接头或十字接头中立板的厚度。表3-27 全熔透对接焊缝及T形接头静载强度设计计算公式角焊缝静载强度计算时焊缝的计算长度一般为实际长度减10mm。......
2023-07-02
曲轴强度设计优化
【摘要】：气体压力在进行燃烧的上止点附近达到最大。在上止点附近活塞的速度很小，可以忽略惯性力Fi，因而在上止点附近活塞上的作用力F达到最大，仅由气体力Fg引起各部位弯曲、扭曲和剪切等应力。图10-10 随曲轴角度的转矩变化1.曲轴销的强度曲轴销（或曲轴）在气体力Fg的作用下，前后主轴承上产生反力R1、R2，如图10-11所示。上式中，如果R1=R2，l1=l，则曲轴销中央部位达到最大。
气体压力在进行燃烧的上止点附近达到最大。在上止点附近活塞的速度很小，可以忽略惯性力Fi，因而在上止点附近活塞上的作用力F达到最大，仅由气体力Fg引起各部位弯曲、扭曲和剪切等应力。
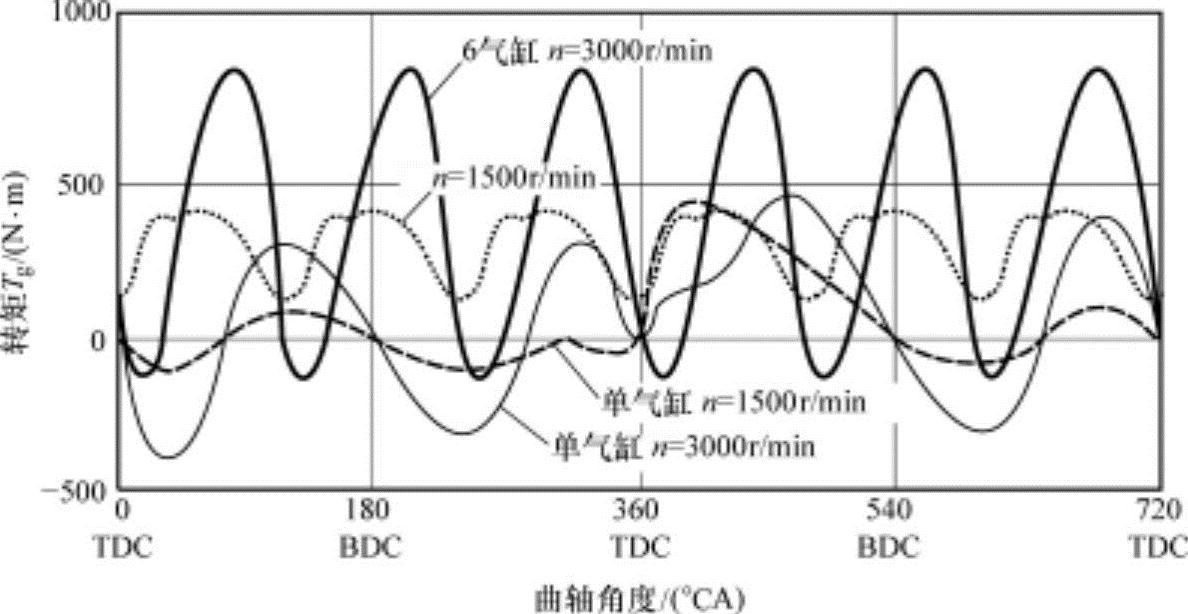
图10-10 随曲轴角度的转矩变化
1.曲轴销的强度
曲轴销（或曲轴）在气体力Fg的作用下，前后主轴承上产生反力R1、R2，如图10-11所示。
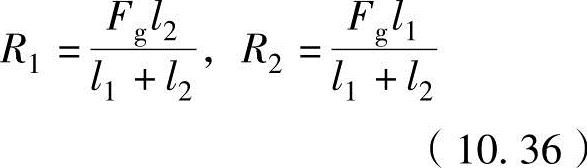
上式中，如果R1=R2，l1=l，则曲轴销中央部位达到最大。中央部位的弯矩Mpb（N·m）的计算式为
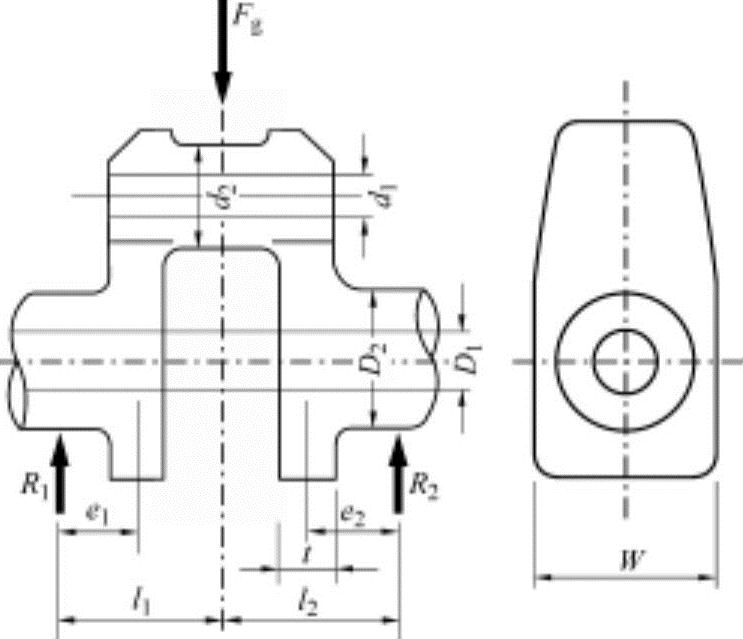
图10-11 曲轴上的作用力
因曲轴销的截面模数为Z=πd3/32≈0.1d（m3），因此曲轴销的弯曲应力σpb（Pa）的计算式为
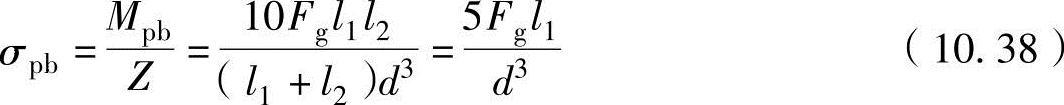
如果曲轴销的端面积为Ac，剪切应力τpS（Pa）的计算式为
因此，合成应力σp（Pa）因曲轴销的弯曲应力和剪切应力互成直角，因此可以用下式计算：
如果曲轴销为内径为d1、外径为d2的中空轴，此时曲轴销的截面模数zh、弯曲应力σphb、剪切应力τphb的计算式为
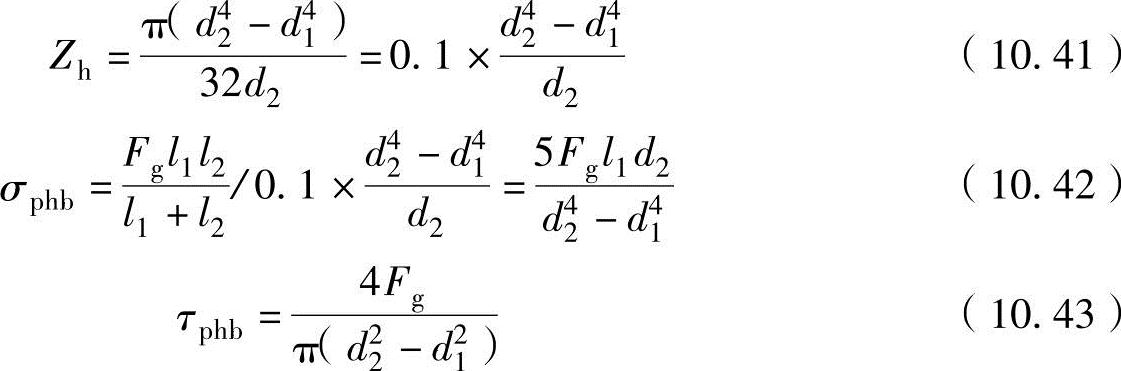
因弯曲和剪切互成直角，中空轴曲轴销的合成应力σph的计算式为
2.曲轴臂的强度
如果图10-11中的曲轴臂宽度为W（m）、厚度为t（m），最大弯矩Mab（N·m）出现在臂的中心位置，则其计算式为
因曲轴臂截面模数Z为Z=Wt2/6（m3），臂的弯曲应力σab（Pa）和压缩应力σac（Pa）的计算式为
合成应力σa（Pa）为
σa=σab+σac （10.48）
有关内燃机学的文章
- 详细阅读
-
梁的弯曲强度条件优化详细阅读
图7-26简支矩形木梁分析：画出梁的弯矩图。根据弯矩图可以看出根据弯曲正应力的强度条件。由图7-27可知，梁中点截面为危险截面，其最大弯矩为由梁的弯曲强度条件经查附录，可选用28b，其Wx=534 cm3。验算梁的强度按有关设计规范，最大工作应力若不超过其许用应力的5%是允许的。已知灰铸铁的Iz=7.56 ×106 mm4，抗拉许用应力[σ] +=39.3 MPa，抗压许用应力[σ] -=58.8 MPa，试校核该梁的强度。根据式故T 形梁强度不足。......
2023-06-19
-
ADAMS车辆工程案例仿真：曲轴设计详细阅读
单击Build > Construction Frame > New命令，结构框创建如图4-7所示；Construction Frame（结构框名称）：crankshaft_reference；Location Dependency：Delta location from coordinate；图4-7结构框Coordinate Reference （参考坐标）：._my_engine.grou......
2023-09-17
-
强度校核：返回导轨优化方案详细阅读
返回导轨与工作导轨不同，施加到导轨上的载荷几乎是固定的，梯级自重载荷Ws均等分布在4个梯级滚轮上，一个梯级距的梯级链重量的载荷Wc均匀分布在梯级主轮上。因返回主轮导轨和副轮导轨是分离设置的，下面以受力较大的主轮返回导轨为例讲解强度校核。要注意的是返回导轨的上曲线段与工作导轨上曲线段类似的法线张力，因此有必要对其进行强度和磨损分析，方法与工作导轨上曲线区段相同。......
2023-06-15
-
设计指标及螺栓连接的强度设计值详细阅读
螺栓连接的强度设计值应按表3.1-4采用。表3.1-1 钢材的强度设计值 （续）注：表中厚度系指计算点的钢材厚度，对轴心受拉构件和轴心受压构件系指截面中较厚板件的厚度。答案：解答：见3.1.4节，不符合规范相关要求。 下列哪一项不属于正常使用极限状态进行设计的内容？......
2023-08-28
-
抗渗强度的确定方法优化详细阅读
无黏性土的抗渗强度主要决定于其颗粒组成。自然界中土的颗粒组成的变化范围很广泛，渗透破坏的型式多种多样，因而在抗渗强度的确定方面至今尚不可能用某一多因素的函数式来表达，目前只能将无黏性土先按渗透破坏型式分类，然后分别给出计算公式。多适用于Cu＞5的土，其抗渗强度计算公式为式中：Gs为土粒密度与水的密度之比，即比重；φ为土体孔隙率。......
2023-06-28
-
圆轴扭转强度的条件优化详细阅读
为了保证圆轴在扭转变形中不会因强度不足而发生破坏，应使圆轴横截面上的最大切应力不超过材料的许用切应力，即式称为圆轴扭转的强度条件。案例6-4 如图6-19 所示的阶梯轴，直径分别为d1=40 mm，d2=55 mm，已知C 轮输入转矩MC=1 432.5 N·m，A 轮输出转矩MA=620.8 N·m，轴的转速n=200 r/min，轴材料的许用切应力[τ]=60 MPa，试校核该轴的强度。......
2023-06-19
-
注塑模强度和刚度校核优化方法详细阅读
分流管注塑模动模垫板和斜导柱强度和刚度的校核是为了控制其变形量，以保证熔体在填充过程中不产生溢料飞边及保证产品的壁厚尺寸，并保证注塑件能够顺利脱模。对注塑模强度和刚度的校核应取受力最大，强度和刚度最薄弱的部位进行校核。由于分流管在注塑模中有三种摆放位置，因此就存在着三种注塑模的结构方案。......
2023-06-30
相关推荐