首页理论教育活塞的运动原理及特点

活塞的运动原理及特点

2025-09-29 理论教育版权反馈

【摘要】：因Sinθ=0为θ=0或θ=180°，表示上止点、下止点，即在止点位置活塞的加速度为最大和最小。最大加速度出现在θ=0的上止点位置，根据式可知amax=ω2r 最小加速度出现在θ=180°的下止点位置，可知amin=-ω2r 加速度a=0的位置就是活塞最大速度umax的位置，如果λ=4，即为θ=77°的位置。

1.活塞的位移

图10-4所示为活塞-曲柄机构的概略图。图中的点O、C、P各为曲轴、曲轴销和活塞销的中心。点A为上止点，点B为下止点。

活塞下降时，假设从上止点A下降的距离为x，曲轴从上止点旋转的角度为θ，连杆的倾斜角度为φ。其中，r为曲轴臂的长度，l为连杆长度。如果把这两个长度的比值定义为连接比λ（=l/r），下式成立：

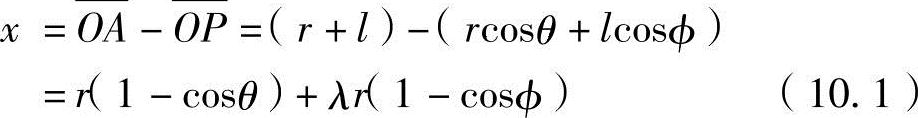
式中，因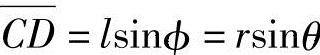，因此

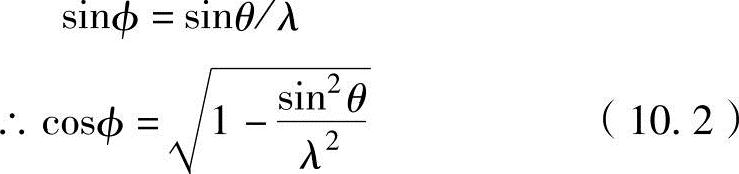
把式（10.2）代入式（10.1），可以推导出

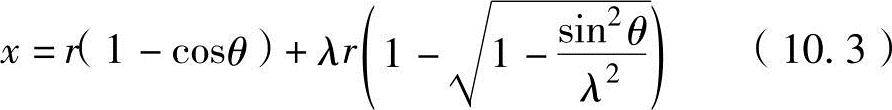
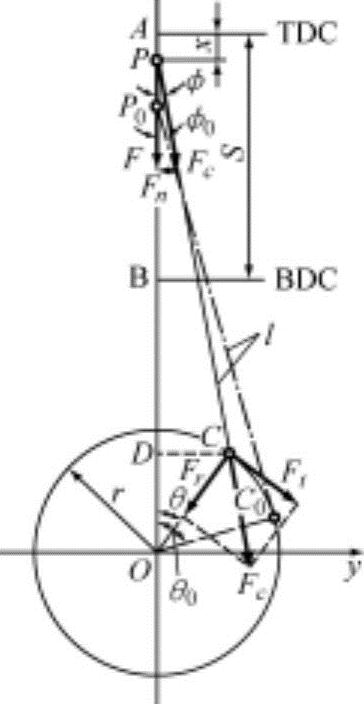
图10-4 活塞-曲柄机构

把式（10.3）右侧第二项利用二项式定理进行展开，因连接比通常为λ=3.5～4.5，并省略1/λ³以上的项，即仅取到第二项，可以用下式近似求出活塞的位移x。

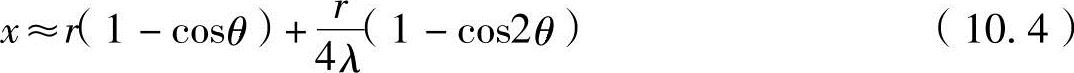
2.活塞的速度

活塞的速度u是对活塞位移x用时间t进行微分的值，可以表示为

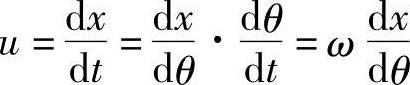
式中，ω（=dθ/dt=2πN/60）为曲轴的旋转角速度（rad/S）。

活塞的位移dx/dθ为对式（10.4）用曲轴角度θ进行微分的值，为

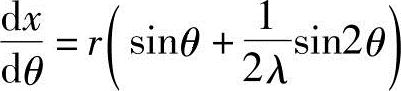
因此，在活塞速度u的式中代入上式和旋转角速度ω，可以推导出

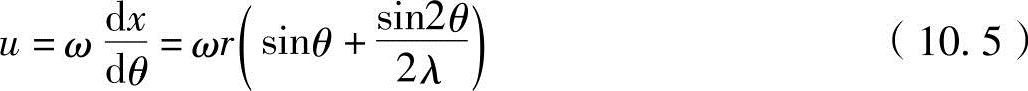
另外，如果发动机的转速为N（r/min），活塞的平均速度u_m（m/S）为

式中，S为行程，S=2r。

现在求出活塞的最大速度和最大速度位置。最大速度应出现在du/dθ=0的位置，对式（10.5）用θ进行微分，可得

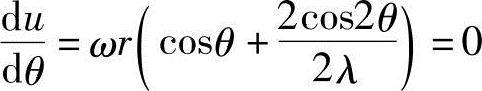
因上式中的右侧括弧项为0，即λcoSθ+coS2θ=0或coS2θ=2coS²θ-1，所以最大速度出现在满足下述条件的曲轴角度上。

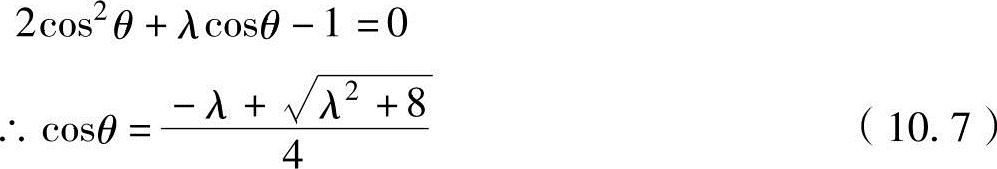
式中，如果假设连接比为λ=4，因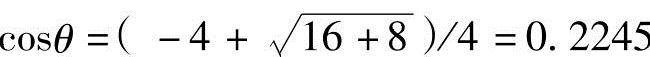，曲轴角度为θ≈77°。此曲轴角度（或出现活塞最大速度的位置）是在λ=4时曲轴臂与连杆之间的角度接近为直角。现在证明其结论。

如图10-4所示，长度l的连杆与曲轴臂轨迹圆的切点，即曲轴臂与连杆成直角的点为C₀，此时活塞的位置为P₀，曲轴角度为θ₀，因三角形OC₀P₀为直角三角形，Sinφ₀=coSθ₀或λrSinφ₀=rSinθ₀，因此下式成立：(https://www.chuimin.cn)

λcoSθ₀=Sinθ₀，tanθ₀=λ

∴θ₀=arctanλ （10.8）

假设λ=4，利用式（10.8）可以求出θ₀≈76°，此角度与利用式（10.7）所获得的θ≈77°相差仅为1°左右，即λ=4时出现活塞最大速度的位置是曲轴臂与连杆之间的角度接近于直角的位置。活塞最大速度u_max的计算，在式（10.5）中代入式（10.8）可以推导出

式中，忽略分子λ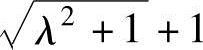中的1，仅考虑λ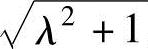，活塞的最大速度为

式中，如果假设λ=4，分母可以看成为1，因此对活塞的瞬间最大速度u_max通过活塞的平均速度式（10.6）和ω=2πN/60，可以得出

u_max≈ωr=ωS/2=πSN/60=πu_m/2≈1.6u_m （10.11）

从上式中可以看出，活塞的瞬间最大速度u_max约为平均速度u_m的1.6倍。

活塞的平均速度u_m可以使用在摩擦损失或气缸内气体速度、气缸壁面的对流热传递等的近似值，大型船舶柴油机为7～9m/S，汽车用汽油机为10～18m/S，小型摩托车发动机可以达到20m/S。

3.活塞加速度

活塞加速度a（m/S²）为对活塞速度u对时间进行微分的值：

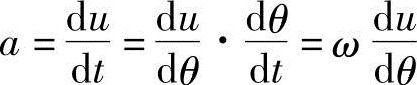
式中，ω=（dθ/dt）为曲轴的转速。

对活塞速度式（10.5）用θ进行微分，可得

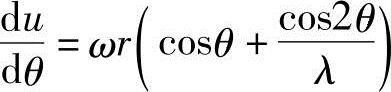
把此式代入加速度式中，可以推导出活塞加速度计算式为

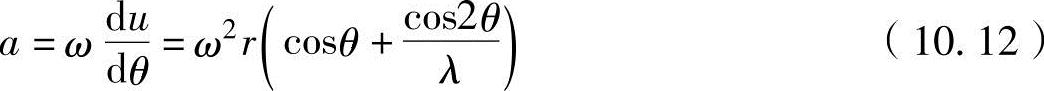
活塞的最大和最小加速度为da/dθ=0，对式（10.12）进行微分，可得

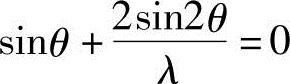
因此，有

Sinθ（1+4coSθ/λ）=0 （10.13）

从式（10.13）中可知Sinθ=0和coSθ=-λ/4。因Sinθ=0为θ=0或θ=180°，表示上止点、下止点，即在止点位置活塞的加速度为最大和最小。另外，如果λ>4，因不存在满足coSθ=-λ/4的θ值，因此表示仅在λ<4时加速度达到最小的位置。

最大加速度出现在θ=0的上止点位置，根据式（10.12）可知

a_max=ω²r（1+1/λ）（10.14）

最小加速度出现在θ=180°的下止点位置，可知

a_min=-ω²r（1-1/λ）（10.15）

加速度a=0的位置就是活塞最大速度u_max的位置，如果λ=4，即为θ=77°的位置。随曲轴旋转角度θ的活塞移动距离x、活塞速度u、活塞加速度a如图10-5所示。