图7-17 气缸和进气系统模型按照对图7-17所示的进气系统长度为L、气缸容积为V的进气系统和发动机模型进行分析。进气系统内气体的容积如同弹簧来回发生改变。图7-19 进气系统长度和发动机转速的关系3.脉动效应惯性效应是利用在进气行程中返回气门附近的最初压力波产生的。因此可以有效地利用进气系统的长度。......
2023-06-28
进气排气过程解释
【摘要】：在解释燃料-空气循环之前，先对理想发动机空气循环的进气、排气过程进行解释。进气、排气过程为定压绝热过程，下面对没有任何损失包括进气、排气阻力的理想过程进行说明。计算：例题2.2的数据如下：T4=2059K，p4=620.32kPa，V4=0.956m3/kg，V6=0.119m3/kg因气缸内混合气为等熵过程，如果假设膨胀到压力下降至大气压，计算得出下述值。残留废气的温度计算如下：3.进气过程奥托循环的进气过程模型如图2-20所示。
在解释燃料-空气循环之前，先对理想发动机空气循环的进气、排气过程进行解释。进气、排气过程为定压绝热过程，下面对没有任何损失包括进气、排气阻力的理想过程进行说明。
1.理想发动机
四冲程理想SI发动机的空气标准理想循环与图2-18相同，理想发动机的工作过程如下：
①可逆绝热压缩过程（1-2）和可逆绝热膨胀过程（3-4）。
②定容燃烧过程（2-3）。
③定容放热过程（4-5）：把在奥托循环中描述的一定比容条件下的放热过程，在理想发动机中以一定的容积和绝热条件下向大气中减压排出（blow-down）废气来代替。
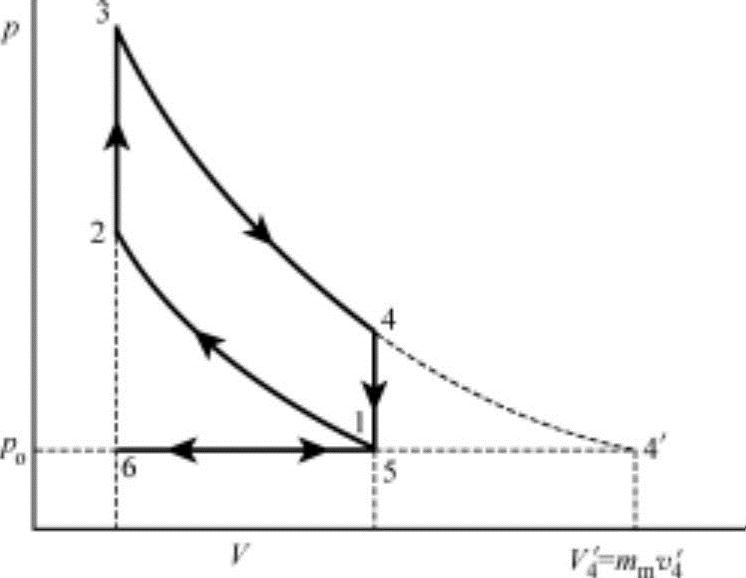
图2-18 理想发动机的p-V线图（WOT）
④定压排气过程（5-6）。
⑤定压进气过程（6-1）：在理想发动机中，新鲜空气的进气在定压绝热过程中进行，这时在燃烧室中的残留废气与新鲜空气混合。
实际发动机的空气燃料理论混合比为，汽油机为14.7，柴油机为20～80。因此，因空气在全部混合气中占有93%～98%，把实际发动机按照工质仅为空气的空气标准循环进行解释也可以预测其性能。表2-7所示为空气的内能和质量热容比。
表2-7 空气的内能和质量热容比
【例题2.2】
空气发动机的压缩比为8，混合空气1kg中新鲜空气为0.97kg，残留空气为0.03kg。此发动机向新鲜空气按照3000kJ/kg比率供给热量。压缩过程初始混合空气的温度和压力分别为60℃和100kPa，请计算下述参数：
（1）各过程末期混合空气的温度和压力。
（2）所做的功、热效率和平均有效压力。
答：
发动机的大小（或混合空气比容）用图2-18中的符号，其计算过程如下：
因压缩比ε为8，压缩后的比容为
（1）各过程末期混合空气的温度和压力计算如下：
①因压缩过程（1-2）末期温度和压力为绝热过程，利用公式Tvκ-1=C和pvκ=C计算出下述值。此时，质量热容比κ值采用了温度333～800K之间的平均值1.376。
T2=T1（V1/V2）κ-1=333×80.376=727K
p2=p1（v1/v2）κ=100×103Pa×81.376=1.74MPa
②在定容加热过程（2-3）中的加热量Q23，因能量守恒定律δQ=dU+pdV中的dV=0，因此空气的内能Δu（=u3-u2）增加。根据表2-7中所列数据计算，当T2=727K时，空气的内能u2为
u2=328.27kJ/kg
Q23=3000kJ/kg×0.97kg=2910kJ
u3=u2+Q23=328.27+2910=3238.27kJ/kg
在表2-7中此值为T3=3763K。由此，压力为
③膨胀过程（3-4）末期的温度和压力用与压缩过程相同的方法进行计算，质量热容比κ采用温度3300K与2000K之间的平均值1.29。
T4=T3（V3/V4）κ-1=3763×（1/8）0.29=2059K
p4=p3（v3/v4）κ=9.07MPa×（1/8）1.29=620.32kPa
（2）所做的功、热效率和平均有效压力计算如下。
①通过表2-7计算温度T1=333K与T4=2059K时的内能u1、u4，发动机所做的功如下：
W=W31-W12=（u3-u4）-（u2-u1）
=（3238.27-1531.03）-（328.27-31.85）=1410.82kJ/kg
②热效率η和平均有效压力pme为
2.排气过程
举例说明奥托循环，在图2-19中显示了p-v线图和T-s线图。排气过程中，在排气门打开瞬间点4位置的废气分为两部分：一部分为继续膨胀的废气；另一部分为从气缸排放的废气。继续膨胀的废气状态向排出的废气施加推动力（或压力）并以等熵过程取得4-4′路径。排放废气的第一部分从点4到点4′高速膨胀。点4′的高速废气在排气管内的一定压力（大气压）作用下，以流动摩擦和扰流抵消，并吸收产生的热量达到最终状态4″。其次，在点4与点4′之间的废气从气缸排放。此部分的废气膨胀到点4′，虽然其速度（比第一部分小）增加，但还是以摩擦方式抵消。最后部分的状态从点4′到点4″继续膨胀。因不可逆节流过程，被排放废气的温度比气缸内的废气温度高，比容增大。因此，点4″位于比点4′比容大的位置。
图2-19 废气排放过程
任意瞬间气缸内的废气质量m，如果知道气缸容积V和废气的比容v，可以容易计算得出。
废气比容通过过程4-4′可以决定。在理想发动机上，排气过程为可逆绝热过程（等熵过程）。
在废气排放结束和重新开始排气过程前，气缸内残留的废气质量如下：
排气过程末期质量me为
式中，me为在燃烧室残留的废气质量；V2，3或6为燃烧室容积；v4′为状态点4′的比容。
残留废气的质量在混合气全质量中所占的比率f为
式中，mm为混合气的全质量，在图2-18p-v线图中，以mm=V4′/v4′进行计算。
混合气的全质量mm在1-2-3-4过程中相同，因此表达式为
将式（2.56c）和式（2.56d）代入式（2.57a），可得
式中，V4′为混合气膨胀到压力达到大气压时混合气全质量mm所占的全容积。
【例题2.3】
计算在例题2.2中发动机燃烧室内残留废气的温度和质量。
计算：
例题2.2的数据如下：
T4=2059K，p4=620.32kPa，V4=0.956m3/kg，V6=0.119m3/kg
因气缸内混合气为等熵过程（κ=1.31），如果假设膨胀到压力下降至大气压，计算得出下述值。
此时，因混合气质量mm=1kg，上述计算得出的容积表示比容。根据式（2.57b），如果假设在排气过程期间废气的状态没有任何变化，残留废气所占的质量比率为
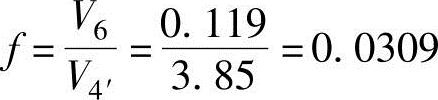
上述计算得出的值与在例题2.2中计算得出的值0.03相似。
残留废气的温度计算如下：
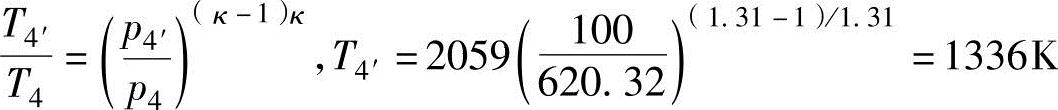
3.进气过程
奥托循环的进气过程模型如图2-20所示。排气过程末期活塞在上止点时，在燃烧室中残留有质量为me的高温废气。残留废气的内能在进气过程初期，即在时间T1（上止点）时为u1。此时，进气门开启，质量为ma、焓为ha的新鲜的空气进入并推动活塞从上止点到下止点，并与残留废气混合，在时间T2（下止点）时，混合气的质量为mm（=ma+me），内能为um。
图2-20 排气、进气过程模型
进气过程时间为Δt=t2-t1。
进气过程为非正常流动过程，进气过程的能量守恒定律可以应用如下：
因进气过程仅有通过进气门进入的流动，Eout为0。另外，假设进气过程为绝热过程，Q也是0。因此，上述公式可以表示为
-W=-Ein+ΔEsys （R12）
在进气过程Δt期间，通过图2-20中进气管a-a端面向气缸内进入的质量为ma空气的能量Ein，如果忽略势能和动能，为内能ua与流动能量pava之和，即
Ein=ma（ua+pava）=maha
在进气过程Δt期间系统能量变化仅为内能变化。
ΔEsys=mmum-meue
把上述两个公式代入式（R12）中，此功与活塞从上止点到下止点所做的功W（=pdV）相同，可以推导出：
式（2.58）就是进气过程的基本公式。下面对全负荷、部分负荷运行条件下的进气过程分别进行分析。
（1）全负荷 全负荷运行条件为节气门全开（Wide Open Throttle，WOT）时的状态。此时，进气过程在一定的压力下进行，进气管压力为理想状态下的大气压pa（或p0）。
参考图2-4的p-V线图，在进气过程0-1期间活塞所做的功为
根据混合气的容积定义V=mv，从上述公式可以推导出：
W=mmp1v1-mep6v6=mmpava-mepeve
根据式（2.57）和上述公式，可得
mmhm=maha+mehe （2.59a）
等式两边同时除以mm，可得
hm=（1-f）ha+fhe （2.59b）
式中，f（=me/mm）为在全部混合气中残留废气所占质量比率，（1-f）为在全部混合气中新鲜空气所占质量比率。式（2.59）是全负荷运行条件下进气过程的理想模型公式。
【例题2.4】
在例题2.1中，如果发动机中进入了压力为大气压（100kPa）和温度为27℃的空气，请问混合气的温度为多少？
计算：
例题2.2 的数据为：
TG=T4′=1336K，f=0.031，p6=p1=100kPa
利用表2-7和表2-8中的数据并通过式（2.59）可以直接进行计算。但是，如果假设质量定压热容为恒定，h=cT，并仅含有空气，可以进行近似计算：
phm=（1-f）ha+fhe
cpTm=（1-f）cpTa+fcpTe
Tm=（1-f）Ta+fTe
Tm=（1-0.031）×300+0.031×1336=332.12K
可以看出，此值与在例题2.2中假设的压缩过程初始温度333K近似。
【例题2.5】
计算例题2.2中发动机的容积效率。
计算：
利用例题2.2、例题2.3、例题2.4中的数据，可以得到下述数据：
从例题2.2得到，混合气空气质量mm=1kg，工作容积Vh=0.837m3，p1=100kPa。
从例题2.3得到，残留废气所占质量比率f=0.031，新鲜空气所占质量ma=0.969kg。
从例题2.4得到，新鲜空气温度Ta=27℃，混合空气温度Tm=60℃。
体积效率ηv定义为气缸内存在的最大空气质量m与新鲜空气质量ma之间的比。气缸内存在的最大空气质量为
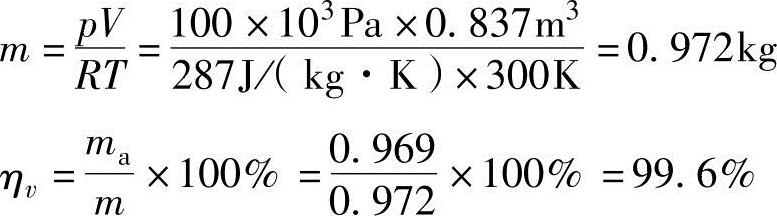
（2）部分负荷 图2-21a所示为部分负荷运行条件下的p-V线图。在部分负荷运行条件下，因节气门的节流作用，进气管内的压力低于大气压。即，新鲜空气的压力低于气缸内的压力。排气过程末期的残留废气状态处在点6的位置。当进气门开启、进气过程开始时，假设在新鲜空气进入之前由残留废气通过绝热膨胀6-6′过程做功，此后活塞下降时新鲜空气和残留废气通过6′-1过程混合。把部分负荷运行条件下的进气过程设定为6-6′-1过程，系统所做的功为
图2-21 奥托循环发动机的理想p-V线图
残留废气通过绝热膨胀6-6′过程所做的功W（=pdV）为（根据式（2.2a）得出W=-ΔU）
W=me（u6-u6′）+p1（V1-V6′）
=me（u6-u6′）+mmp1v1-mep6v6′
把上述公式代入式（2.57）中，有
mmhm=maha+meh6′ （2.60a）
hm=（1-f）ha+fh6′ （2.60b）
在式（2-60b）中，下标a为进入到气缸内的新鲜空气；下标m为进气过程末期新鲜空气和残留废气混合的混合气；下标6′为残留废气绝热膨胀到进气压力后的状态。式（2.59）是以进气门开启时刻晚为前提条件的。如果进气门在活塞到达上止点之前开启，残留废气首先膨胀进入到进气管内（逆流）后，重新与新鲜空气一起进入到气缸内。此时，路径类似于6-6″-1，在进气过程所做的功W用p1（V1-V6）得出。考虑上述所解释内容和式（2.57），可以得出
W=p1（V1-V6）=p1（mmv1-V6）=p1mav1+p1mev1-p1V6
mmhm=maha+meu6+p1V6 （2.61a）
hm=（1-f）ha+f（u6+p1v6） （2.61b）
实际上，残留废气通过不可逆膨胀进入到进气管内会造成损失，但在这里没有考虑此损失。
（3）增压发动机增压发动机的进气过程在进气管内压力高于大气压的高压状态下进行。图2-21（b）显示了增压发动机的理想p-V线图。其中，p1（=p6′）表示增压压力，p5（=p6）表示排气压力。对于增压发动机的增压功应用能量守恒定律，与式（2.60）相同。
有关内燃机学的文章
- 详细阅读
-
进排气门气体流动优化详细阅读
发动机的容积效率与气门的大小、数量和气门正时等有关。气门通道面积、升程 气体通过气门的面积Av为气体通过气门时的最小端面积。图7-10 流量系数测量实验装置图7-11 进气门的流动特性排气门的升程对流动特性的影响如图7-12所示。因此，进气门、排气门的流量系数应以动态流量系数来定义并进行计算。图7-12 排气门的流动特性②动态流量系数。......
2023-06-28
-
分层进气发动机的优化设计详细阅读
分层进气发动机的工作原理：在火花塞附近供给可燃混合气，在燃烧室内供给稀薄混合气，总体上在稀薄混合气状态进行燃烧。为了解决这个缺陷，分层进气发动机气缸内的混合气并不全部为均匀混合气，而仅在火花塞附近为理论空燃比混合气的方式。其他分层进气发动机有IFP方式、布罗德森方式、福特缸内直喷燃烧方式等。分层进气发动机的优点：①能宽范围控制燃烧，因此可大幅度降低有害废气的排放量。......
2023-06-28
-
国Ⅲ柴油机进、排气系统导致动力不足故障诊断详细阅读
导致进气不足的主要原因有以下几点：①空气滤清器堵塞，进气管路上的橡胶软管被压瘪或内部起皮或被其他异物堵塞。由于空气滤清器及进气管道系统因素导致柴油机动力不足故障的诊断与排除详见表2-2。柴油机的排气制动系统一般采用关闭柴油机排气通道的办法，使柴油机活塞在排气行程时，受气体的反压力，进而阻止柴油机的运转而产生制动作用，达到控制车速的目的。......
2023-09-19
-
进气角度对气流运动的影响详细阅读
从图6.32也可以看出，随着进气角度的增加，进气口周围的气流越来越集中，在进气角度30°时，进气口周围的涡团几乎把进气口包围起来，并且涡团半径有变大的趋势，占据了进气口两侧的空间。虽然涡团的半径减小，但是由于进气角度的增加导致进气气流速度明显增强，从而随着进气角度的增加涡团强度明显增强。......
2023-06-23
-
东亚地区合作的过程建构：关系与过程书解释详细阅读
过程建构主义是一种动态理论。在这种情况下，保持东亚地区多边主义合作的过程比取得立竿见影的结果更重要。以过程为主导的东亚地区多边主义从一开始便是以合作为导向的，并不断将不同的行为体，包括地区大国，纳入这一进程之中。......
2024-01-10
-
发动机进气增压系统解析详细阅读
发动机一般采用自然进气，它利用活塞下移形成的真空度将空气吸入气缸。由于自然进气是比较被动的进气方式，进气效率不高，这影响发动机功率的发挥，为了提高发动机功率，进气增压系统应运而生。奥迪A6 3.OTFSI 发动机采用的机械增压器就属于改进型的罗茨增压器，它的2个转子上均有4个螺旋形叶片。2．涡轮增压系统涡轮增压系统的结构与原理涡轮增压器的驱动力来源于发动机排出的废气，增压器要在发动机达到一定转速后才工作。......
2023-08-23
-
稀薄燃烧的进气通路设计及优势分析详细阅读
稀薄燃烧发动机的进气通路有两个：一个是直线形端口，另一个是螺旋形端口。即使是稀薄燃烧发动机，仅在一定的区间内以稀薄空燃比进行控制，一旦超出此区间，以理论空燃比进行控制。图5-47 随涡流的湍流生成和稀薄燃烧的改善稀薄燃烧效果 稀薄燃烧发动机因稀薄燃烧时燃烧温度降低，降低了冷却损失，减少了质量热容比，从而提高了热效率。......
2023-06-28
相关推荐