在一般情况下,变形毛坯内各质点的变形和受力状态是不相同的。通常将质点的受力状态称为点的应力状态。对同一点应力状态,6个应力分量的大小与所选坐标有关,不同坐标系所表现的6个应力分量的数值是不同的。对于板料冲压工艺,第二行应力状态居多。......
2023-06-26
虽然供给到气缸内的热量(Q1)以燃料的放热量(mfHi)来进行计算,但在一般情况下,加热量、放热量、膨胀功和压缩功以工质的状态变化量来进行计算。
首先要导出行程中计算做功的计算式。现在,假设气缸内高压状态1(p1、v1)的1kg气体膨胀到低压状态2(p2、v2)。此过程在图2-1p-v关系线图中以路径1→2表示。在此过程中,单位质量气体所做的功可以计算为

式中,压力为绝对压力,始终大于0;体积为v2>v1,因此所做的功为正(+);S1234为面积。在能量单位中,符号表示方向,做功符号为正(+),表示系统(工质)向周围(外部)所做的功。因此,在此过程中,工质随着体积的增大,对外做功,我们把它称为膨胀功We。其中下标e表示膨胀。
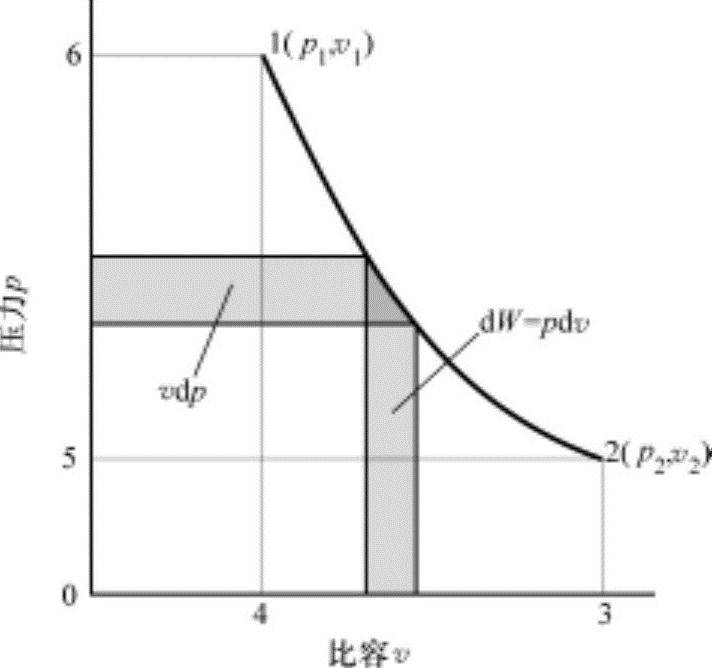
图2-1 p-v关系线图
活塞反方向移动,压缩气体从低压状态2到达高压状态1,此时所做的功W可以计算为
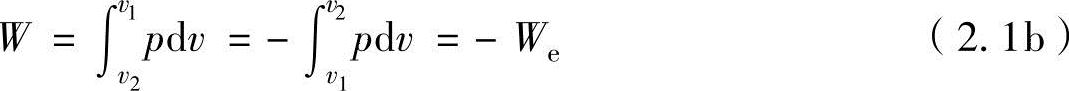
因膨胀功We为正,因此功W为负。功W的(-)符号表示外部向系统做功。在此功的作用下,气体被压缩,因此称为压缩功Wc。其中下标c表示压缩。在此可以知道相同的两个状态之间的膨胀功We和压缩功Wc大小相同,方向相反。
然后,要对加热量和放热量进行计算。气体状态在图2-1中从状态1变换到状态2时,向单位质量工质供给的热量q1可以利用下述能量守恒定律公式进行积分计算:
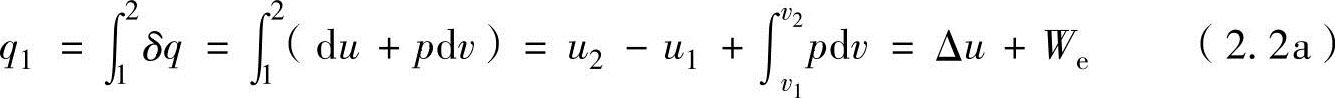
从上述推理可以得知,热量Qe作用在内能变化Δu(=u2-u1)和膨胀功We。
这次,以相反的方向进行计算。气体状态从状态2变换到状态1,气体被压缩时,可计算压缩功Wc与放热量Qe之间的关系为:
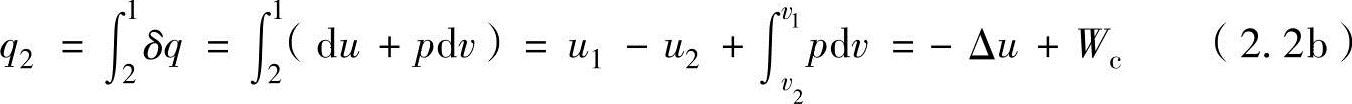
从上述推理可以得知,压缩功We作用在内能变化Δu(=u2-u1)和放热量Q2。
1.定容过程
在体积一定的定容状态(v0=v1)时的变化在图2-2p-v关系线图中以垂直线0→1路径表示。在定容过程中dv=0,式(2.1)中的W=0,因此没有膨胀功和压缩功。但是在定容过程中热量减少,从式(2.2)可以得知,热量的传递导致内能的变化,即温度的变化。
在定容过程中,对于理想气体的状态变化,下式成立。
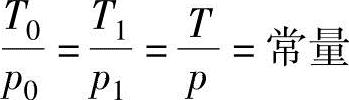
在图2-2中从状态0到状态1为定容过程。当压力下降时,气体传热q与式(2.2)的内能变化量相等,即
q1=u1-u0=cv(T1-T0) (2.3)
上式中,cv为质量定容热容,假设为常量。
2.定压过程
在压力一定的定压状态(p0=p2)时的变化在图2-2p-v关系线图中以水平线0→2路径表示。在定压过程中,对于理想气体的状态变化,下式成立:
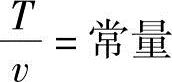
在图2-2中从状态0到状态2为定压过程,对于其膨胀功利用式(2.1)导出下式加以计算。

在定压过程中的气体传热q,根据式(2.2)可以导出下式中的任一项加以计算:
q=u2-u0+p(v2-v0)=h2-h0=cp(T2-T0)
(2.5)
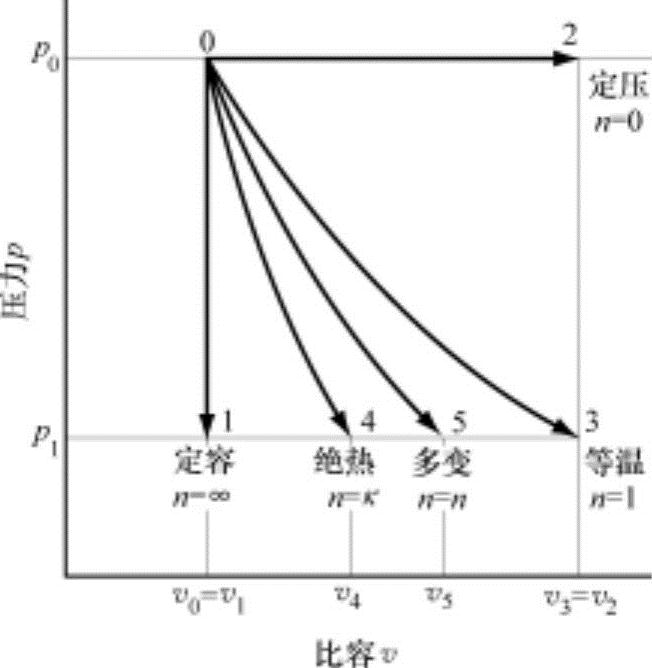
图2-2 各种状态变化的q-v线图
3.等温过程
等温过程(T0=T3)在图2-2中以直角双曲线0→3表示。理想气体的内能u与焓h为温度的函数,在等温过程中这些变量不变,即u3=u0、h3=h0。在等温过程中,对于理想气体的状态变化,下式成立。
pv=常量
利用式(2.1),可以导出如下的在等温过程中从状态0到状态3的膨胀功计算式:
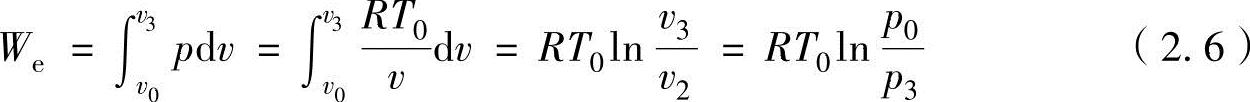
在等温过程中的气体传热q,根据式(2.2)导出下式加以计算:

即,因在等温过程中没有内能的变化,气体传热q直接转换为膨胀功We。相反,压缩功全部转换为外部功,这表示等温压缩热全部被散发到外部。
4.绝热过程
绝热过程表示气缸内的气体与周围之间没有热传导,即δq=0。在图2-2所示的p-v关系线图中,绝热过程线以比等温过程的直角双曲线斜度更大的0→4路径表示。在绝热过程中,压缩功全部转换为热量,使气体温度(或内能)上升。相反,膨胀功表现为气体温度(或内能)下降。
在绝热过程中理想气体的状态变化公式如下:
pvκ=常量
Tvκ-1=常量 (2.8)
Tp(1-κ)/κ=常量
绝热膨胀过程中的膨胀功计算,在式(2.1)中把压力p用p=p0v0κ/vκ代替可以导出下式:
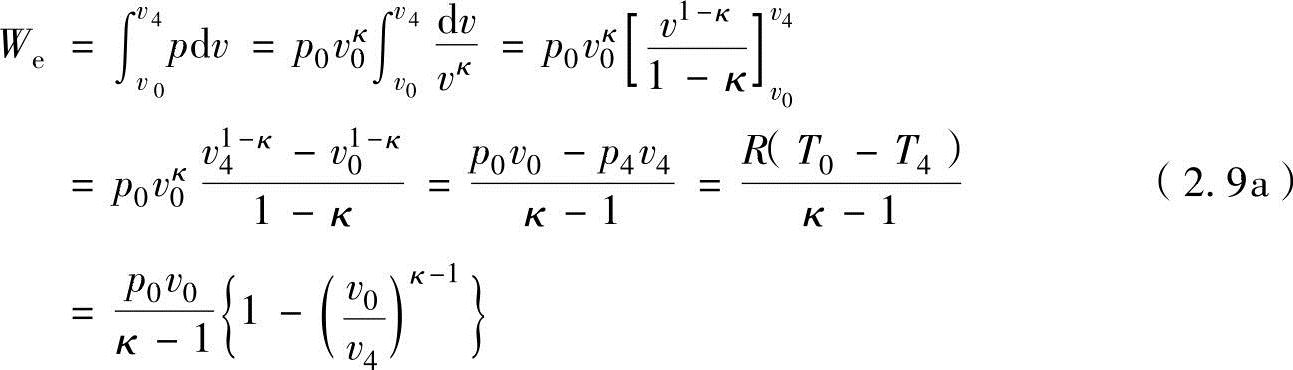
在往复式发动机中的膨胀功We,因压缩比ε在图2-2的绝热过程中定义为ε=v4/v0,因此根据式(2.8a),可以导出下式:
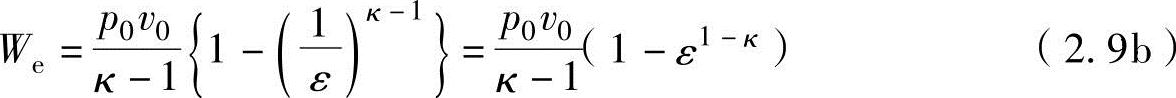
5.多变过程
在实际内燃机中,因气缸内气体与外部存在温度差,始终进行热量的传递过程,因此不可能实现绝对的等温过程或绝热过程。尤其是,即使在相同的冲程中,随着活塞位置(或气体比容)的不同,其热传导量也不同。如,在压缩过程中,初期因气缸内气体的温度为常温(20°C)程度的低温状态,因此从活塞、气缸等部件中吸收热量,但到了后期,因气体被压缩温度上升,处于高温状态,通过气缸壁等放出热量。另外,在膨胀过程(做功过程)中,初期因气缸内的燃烧气体处于高温状态,向活塞、气缸、进排气门等放出热量。这表示实际的压缩过程和膨胀过程既不是绝热过程,也不是等温过程。
虽然在相同的工作过程中热传导量有所变化,但解释此工作过程时,把在此工作过程期间的热传导量看成为均等,以此用下式表达工质的状态变化公式:
pvn=常量(n≠κ≠1)
把上述公式表达的状态变化称为多变过程,把n称为多变指数(或绝热指数)。在实际发动机中,根据运转条件,抽取任意值测试取得多变指数,但在以上所述的各状态变化中,具有特定值。如,在定容过程中n=∞,在定压过程中n=0,在等温过程中n=1,在绝热过程中n=κ。在实际过程中,抽取绝热过程和等温过程的中间值。即多变指数n在1<n<κ之间变化,多变过程在图2-2p-v关系线图中以0→5路径表示。根据式(2.9),用下式表达多变过程中的理想气体的状态变化公式:
pvn=常量
Tvn-1=常量
Tp(1-n)/n=常量(2.10)
式(2.10)表示,在绝热过程中理想气体的状态变化公式中,用多变指数n置换质量热容比κ的形态。
从状态0变化到状态5时的多变过程膨胀功We的计算式为,在绝热过程膨胀公式(2.8)中,用多变指数n置换质量热容比κ的形态,即,

现在计算一下多变指数n和热量q之间的关系。首先对理想气体状态方程pv=RT进行微分计算,得出dv/v方程式,并把多变过程关系式(2.10)进行微分得出的dp/p代入到本方程式中,得出下述方程:

从上式中推导出:
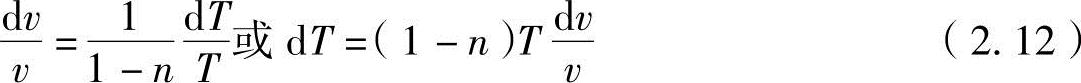
把式(2.12)中的dT代入到能量守恒公式δq=cvdT+pdv中,可以得出:
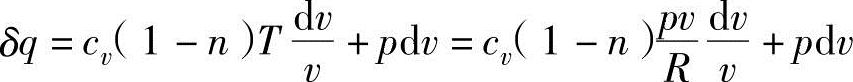
从上式可以推导出:
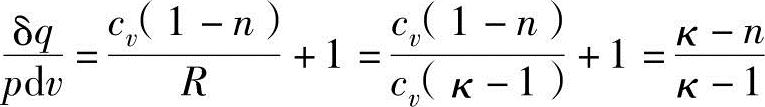
把上式中的pdv用能量守恒公式pdv=δq-cvdT代入,可以推导出:

因此,对于状态0到状态5的多变过程中的传热量q,对式(2.13)进行积分,可以得出:

式中,把过程中的质量定容热容cv、质量热容比κ、多变指数n看成常量。
有关内燃机学的文章

在一般情况下,变形毛坯内各质点的变形和受力状态是不相同的。通常将质点的受力状态称为点的应力状态。对同一点应力状态,6个应力分量的大小与所选坐标有关,不同坐标系所表现的6个应力分量的数值是不同的。对于板料冲压工艺,第二行应力状态居多。......
2023-06-26

下面以直流系统两侧交流节点母线电压发生变化时直流系统的运行状态变化情况为例,假定换流变压器的标准变比在交流侧,说明直流系统运行方式转换过程[7~9]。如果Uti继续下降,最终会导致直流系统的停运。当γ增大一定程度后,导致换相失败,直流系统停运。图3.11直流系统控制方式的转换......
2023-06-29

它是以什么形式存在,则是热力学要回答的问题。热力学主要研究的是系统的平衡及气体体积变化的现象。热力学平衡态在热力学系统中,根据系统和外界的关系可以分为孤立、封闭、开放三类系统。满足上述三种平衡条件的系统,就称系统处于热力学平衡态,简称平衡态或平衡。非平衡态和状态参量在热力学中,系统处于两端有各自不同恒温的状态为非平衡态。有关理想气体状态方程的内容,已远离本书的宗旨,故这里不予多述。......
2023-06-19

由于单个的汉字只代表汉语的一个音节,两个汉字才记录汉语的一个双音节词,这样,汉字与汉语词的关系更不是一对一的了 。可是在上述情况中,单个汉字却不是单独、直接成词的,也就是说,汉字在它服务于汉语的历史过程中,部分地改变了自己的性质。总而言之,尽管汉语由于社会和历史的原因而不断发展、不断变化,而汉字也能随之发生变化而适应汉语的发展。纵观汉字和汉语关系的全部历史,二者基本上是和谐的。......
2024-01-26

这是因为,与原来的平衡状态相比,转速升高的比率远小于电压上升的比率的缘故。当到达B点时,电动机转矩重又减小为TMA,又和负载转矩TLA处于平衡状态,但这时的转速已经增大为nB了。需要说明的是,这里所说的“电压升高”,是指电压在允许范围内的升高。也就是说,由电压升高引起的磁通增大,并不足以使磁路饱和。......
2023-06-24

当负载转矩由TLA增加至TLC时,由于电动机的转矩小于负载转矩,故转速下降。而机械特性曲线表明,在转速下降的同时,电动机的电磁转矩TM将增加,一直增加到TMC=TLC时,重又处于平衡状态。......
2023-06-24

AutoCAD提供了一组图层状态控制开关,用以控制图层的实体的可见性和可操作性。图层的状态控制既可以通过设置,又可以通过工具栏设置。位于关闭图层上的图形是不可见的,也不可被打印,但可以重生成,可以被某些选择集命令选择并修改。......
2023-06-21

第六条缔约国的法律规定个人丧失或被剥夺该国国籍时其配偶或子女亦丧失该国国籍者,其配偶或子女国籍的丧失应以具有或取得另一国籍为条件。六、除本条所述的情况外,任何人如丧失缔约国国籍即无国籍时,应不丧失该国国籍,纵使此项国籍的丧失并没有为本公约的任何其他规定所明确禁止。......
2023-07-24
相关推荐