光波在交界面的反射和折射现象分析

2023-06-27 理论教育版权反馈

【摘要】：式（5-1）即为反射定律和折射定律，又称斯涅尔定律，这两个定律可以从平面电磁波在不同媒质的平面分界上的反射和折射现象得到严格的证明。满足n1sinθ1/n2=1的入射角为全反射的临界角，记为θc，则有图5-4光波在两种介质交界面的反射和折射当入射角θ1＞θc时，光线在分界面上发生全反射，这是用几何光学描述均匀光波导中光线传播特点的一个重要结论。

光波属于电磁波的范畴，在均匀介质中传输时，其轨迹是一条直线，当光射线射到两种介质交面时，将发生反射和折射，如图5-4所示，从介质n1入射到介质n2的光信号的能量一部分反射回介质n1，一部分透射到介质n2。且θ1、θ2、θ′1满足以下关系

pagenumber_ebook=79,pagenumber_book=73

式中 n1——纤维折射率；

n2——包层折射率；

θ1——入射光线与界面垂直线之间的夹角（入射角）；

θ′1——反射光线与分界垂直线之间的夹角。

式（5-1）即为反射定律和折射定律，又称斯涅尔定律，这两个定律可以从平面电磁波在不同媒质的平面分界上的反射和折射现象得到严格的证明。

1.全反射定理

由斯涅尔定律可以得到，折射角θ2=arcsin（n1sinθ1/n2），如果n1＞n2，则在n1sinθ1/n2=1时，折射角θ2=90°，当n1sinθ1/n2＞1时，θ2无实数，这就意味着发生了全反射。满足n1sinθ1/n2=1的入射角为全反射的临界角，记为θc，则有

pagenumber_ebook=79,pagenumber_book=73

图5-4　光波在两种介质交界面的反射和折射

当入射角θ1＞θc时，光线在分界面上发生全反射，这是用几何光学描述均匀光波导中光线传播特点的一个重要结论。显然，只有n1＞n2时，从折射率为n1的媒质中入射的光线才可能发生全反射。

光线在不同媒质的分界面上发生反射和折射时，除了满足反射和折射定律以外，另一个重要特点是保持其极化状态不变，也就是说，如果入射光是水平垂直极化波（电场强度与入射面平行），则反射光和折射光也都是垂直极化的。

2.数值孔径

对电信号而言，只要把放大器的输出端与传输线连接起来，电信号就被送入线路，而对光通信来说，情况就比较复杂。入射在光纤端面上的光，其中一部分是不能进入光纤的，而能进入光纤端面的光也不一定能在光纤中传输。只有符合某一特定条件的光才能在光纤中发生全内反射而传播到远方。

如图5-5所示，根据斯涅尔定律应有

式中 n1——纤芯折射率；

n0——光纤端面之外介质的折射率。

如果端面之外是空气，则n0=1。入射光线成为束缚光线的条件是θ2＜90°-θc，sinθ2＜cosθc。也就是

pagenumber_ebook=80,pagenumber_book=74

于是得到

从式（5-4）可以得到一个重要结果：从空气中射到光纤纤芯端面上的光线被光纤捕获成为束缚光线的最大入射角θmax必须满足以下条件

pagenumber_ebook=80,pagenumber_book=74

定义上述光线成为束缚光线的最大入射角的正弦，即sinθmax为光纤的数值孔径，记为NA，即

数值孔径NA是光纤的一个极为重要的参数，它反映光纤捕捉光线能力的大小。NA越大，光纤捕捉光线的能力越强，光纤与光源之间的耦合效率就越高。从这个意义上讲，光纤的相对折射率差Δ应取得大一些，但Δ过大会使光纤的多径色散严重。实际的光纤总有Δ≪1，多模光纤的数值孔径一般在0.2左右。

3.传播时延和时延差

图5-5中光线的传播路径与包层和纤芯界面的两个交点P、Q间的距离设为LP，纤芯的半径为a，由几何关系可得

其光程为L0，则

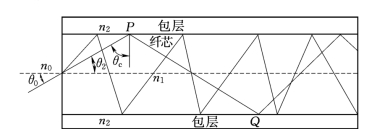
pagenumber_ebook=80,pagenumber_book=74

图5-5　光纤的导光原理

P、Q两点之间的路径在光纤轴上的投影长度为ZP，则

光线沿Z轴方向传播单位距离的传播时延为

pagenumber_ebook=81,pagenumber_book=75

式中 C——光在真空中的传播速度。

由式（5-10）可以得到一个重要结论：阶跃光纤中光线的传播时延在纤芯折射率n1一定时仅与光线与Z轴间的夹角θ2有关。在Z轴方向传播单位距离，具有不同倾斜角θ2的束缚光线的最大时延差（临界角行进的光线与沿中心轴线行进的光线的时延差）为

pagenumber_ebook=81,pagenumber_book=75

4.比特率距离积

光纤通信系统的容量通常可以用比特率距离积表示，其含义是如光纤通信系统发送的数据速率为X （Mbit/s），能够在光纤中传输Y km，其比特率距离积为XY （Mbit/s—km）。那么，同样的系统则能传送数据比特率为X′ （Mbit/s）的信号Y′km，只需满足X′Y′≤XY。

由于不同的光线在光纤中传输时间不同，因而输入一个光脉冲，其能量在时间上相对集中，经光纤传输后到达输出端，输出一个光脉冲，其能量在时间上相对弥散，这种现象称为模式色散。

假设系统的比特率为B，一个粗略的判据是只要光脉冲在时间上的展宽不超过系统比特周期1/B的1/2，即 pagenumber_ebook=81,pagenumber_book=75 ，则模式色散有如下的限制

因而光纤通信系统由于受模式色散的影响，其比特率距离积为

如Δ=0.01，n1=1.5 （≈n2），可得BL＜10 （Mbit/s—km），如图5-6所示。由以上分析可知，Δ是一个很重要的物理量。比特距离积与Δ成反比，而数值孔径NA 与Δ成正比，因而如何合理地选择Δ十分重要，为了减小模式色散，提高系统的传输速率，Δ越小越好，Δ 典型值为0.01，这样NA 就很小。必须采取合适的方法增加光源和光纤之间的耦合，如可以将光纤的入射端口烧制成球形端面，它可以明显地增大光纤的数值孔径，在光源和光纤之间加圆柱形光纤透镜或自聚焦透镜都可以使光束的发散角变小，从而提高耦合效率。

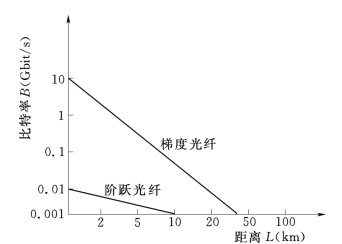
pagenumber_ebook=81,pagenumber_book=75

图5-6　色散引起的比特率距离积极限n1=1.5，Δ=0.01

梯度光纤由于其纤芯的折射率分布渐变，从纤芯的最大值渐变到纤芯和包层界面处的最小值，因而沿中心轴线的光线其传播速度最慢，沿纤芯和包层分界面上全反射行进的光线速度最快，虽然中心轴线光线在同样的光纤长度上行进的路程短，但速度较慢；而全反射光线行进的路程长，但速度较快，使两者之间的时间差变小，模式色散较小。目前使用的多模光纤都是梯度光纤。

对于折射率成抛物线分布的梯度光纤，在光纤上传输距离为L时，最快光线和最慢光线时延差为

pagenumber_ebook=82,pagenumber_book=76

梯度光纤大大降低了模式色散，提高了系统的容量，即比特率距离积，但如果彻底地消除模式色散，必须选择一种纤芯远小于或与工作波长相当的光纤，这样的光纤称为单模光纤（这是一种粗略的定义）。多模光纤中光线的不同路径可看作不同的模且光能量由这些模共同携带向前传播，单模光纤中光线只是一条沿中心轴线的路径，因而只有一个模携带光能向前传播。

当纤芯的半径与工作波长可以比拟时，如单模光纤，光线被限制在纤芯中向前传输不能再归功于其内部的全反射。光在单模光纤中的传输可采用波动理论法进行定量的描述，波动理论分析法是一普遍方法，可用来分析任何纤芯半径的光纤，几何光学分析法是波动理论分析法在光波长远小于光纤纤芯半径时的一种近似。

光波在交界面的反射和折射现象分析

相关推荐