循环码的基本概念与码多项式

2023-06-27 理论教育版权反馈

【摘要】：循环性是指循环码组中的任一许用码字循环左移后所得到的码字仍为该循环码组中的一个许用码字。C1C0]是码长为n的循环码中的一个码字，对其进行循环左移、右移，无论移动多少位，得到的结果均为该循环码中的一个码字。为了便于用代数学的理论分析计算循环码，把循环码中的码字用多项式来表示，称为码多项式，它是把码字中各码元的取值作为码多项式的系数。循环码的多项式符合下列定理。

循环码是线性分组码中重要的一类，它是在严密的代数学理论基础上建立起来的。循环码的编码设备通过反馈移位寄存器就可以实现，比较简单。其检错纠错能力也较强，因此在实际中得到了较大地发展。

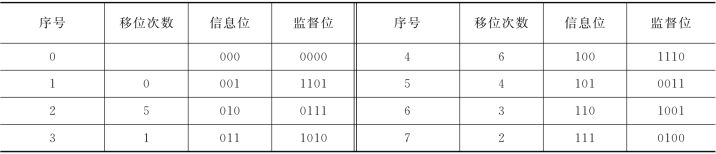
循环码是一种线性分组码，它除了具有线性分组码的封闭性之外，还具有循环性。通常，前k位是信息码元，后r位为监督码元，具有系统码的形式。循环性是指循环码组中的任一许用码字（全 “0”除外）循环左移（或循环右移）后所得到的码字仍为该循环码组中的一个许用码字。设码字矢量C= [Cn-1Cn-2…C1C0]是码长为n的循环码中的一个码字，对其进行循环左移、右移，无论移动多少位，得到的结果均为该循环码中的一个码字。如式（4-36）中的各码字均为该循环码中的一个码字

pagenumber_ebook=70,pagenumber_book=64

表4-6　列出了一种（7，3）循环码的全部许用码字。

pagenumber_ebook=70,pagenumber_book=64

为了便于用代数学的理论分析计算循环码，把循环码中的码字用多项式来表示，称为码多项式，它是把码字中各码元的取值作为码多项式的系数。对于码字矢量C= [Cn-1Cn-2…C1C0]用码多项式表示为

式中 x i——码元位置的标记，表示由其系数所决定的码元取值所处的对应位置。

码元位置系数只能取0或1，运算时其系数的运算为模2运算。如码字1001110，0011101用码多项式分别表示为

则T1（x）+T2（x）=x 6+x 4+x+1（即1001110⊕0011101=1010011）。

在整数的按模运算中，常用是模2运算，如1+1≡0 （模2）、1+2≡1 （模2）等。对于模n运算，如果一个整数m可以表示为式中 Q——整数；

pagenumber_ebook=70,pagenumber_book=64

p——m被n除后的余数。

在多项式中，同样可以用类似的模运算。如

式中 N（x）——幂次为n的多项式；

Q（x）——商；

r（x）——幂次低于n的余式，多项式的系数在二元域上。

式（4-41）可写为

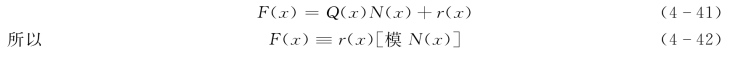
pagenumber_ebook=71,pagenumber_book=65

如x 3被（x 3+1）除可得余式为1，则

同理有x 4+x 2+1≡x 2+x+1 （模x 3+1）。循环码的多项式符合下列定理。

定理一：若T（x）是长为n的循环码中某个许用码组的码多项式，则x iT（x）在按模x n+1运算下，也是该循环码中一个许用码字的码多项式。

如（7，3）循环码中许用码组0011101的码多项式为T（x）=x 4+x 3+x 2+1，则

x 3T（x）≡x 6+x 5+x 3+1（模x 7+1），x 6+x 5+x 3+1对应的码字为1101001，它是该（7，3）循环码中的一个许用码组，而且它是上述循环码0011101左移3次后形成的。

定理证明：设T（x）=Cn-1x n-1+Cn-2x n-2+…+C2x 2+C1x+C0，则

pagenumber_ebook=71,pagenumber_book=65

其中，ri（x）=Cn-1-ix n-1+Cn-2-ix n-2+…+C0x i+Cn-1x i-1+Cn-i。它是T（x）左移i位后形成的码字。若把i取不同的值重复做上述运算，可得到该循环码的其他许用码字。所以，码长为n的循环码的每一个许用码都是按模x n+1运算的余式。如果已知码多项式T（x），则相应的循环码就可以由x iT（x）按模x n+1运算的余式求得。

循环码的基本概念与码多项式

相关推荐