离散无记忆信源编码（DMS）

2023-06-27 理论教育版权反馈

【摘要】：假设离散无记忆信源输出有限个符号xi，i=1，2，…离散信源编码就是对每个符号用一定长度的代码来表示。在信息论中已经证明，每个符号的二进制代码平均长度最短不应小于信源的熵。设信源共有L种符号，则需要的编码长度N 由log2L决定。当符号等概出现，但L不为2的整数次幂时，信源的平均信息量H与编码长度N 之间最多相差1bit。为了提高编码效率，对符号出现概率不相等的信源采用不等长编码。

假设离散无记忆信源输出有限个符号xi，i=1，2，…，L，每个符号出现的概率分别为P（xi），i=1，2，…，L。该信源的熵（平均信息量）为

式（3-5）中，P（xi）相等（等概）时，等号成立。

离散信源编码就是对每个符号用一定长度的代码来表示。在信息论中已经证明，每个符号的二进制代码平均长度最短不应小于信源的熵。各符号的代码长度可以等长，也可以不等长。编码方法不同，编码的效率也不同。

1.等长编码

等长编码（也称均匀编码）就是不管符号出现的概率如何，每个符号都用N 位二进制码表示。设信源共有L种符号，则需要的编码长度N 由log2L决定。当L为2的整数倍次幂时，有

当L不为2的整数次幂时，则应取

式中 [log2L]——取log2L的整数部分。

定义DMS编码的效率为H（x）/N，即每位二进制码所代表的信源的平均信息量。由式（3-5）～式（3-7）可知，当符号等概出现且L为2的整数次幂时，N=H（x），这时的编码效率为100%。当符号等概出现，但L不为2的整数次幂时，信源的平均信息量H（x）与编码长度N 之间最多相差1bit。因此，当L≫1时，编码效率下降不严重，当L值较小时，编码的效率较低。为了提高编码的效率，可将连续J个符号进行统一编码，这种方法称为扩展编码。显然扩展编码时必有L J个不同的码字，这样每个码字的编码长度N 为

对N 取整数有

这时每个信源符号的平均位数为

由式（3-10）可见，扩展编码后使式（3-7）中每个符号所增加的1bit下降到了1/J bit，从而提高了编码效率。

2.不等长编码

在上述的讨论中，如果符号出现的概率P（xi）是不相等的，那么用等长度编码时效率会更低。为了提高编码效率，对符号出现概率不相等的信源采用不等长编码。这种编码方式是将出现概率较大的符号用位数较短的二进制码字表示，而出现概率较小的符号用位数较长的二进制码字表示，即不等长编码是一种概率匹配编码。哈夫曼码就是一种最佳的匹配编码，它是一种单义可译码，是一种平均长度最短的码。

假设哈夫曼编码中，出现概率为P（xi）的符号的编码长度为ni，则每个符号的平均码长为

可以证明，每个符号的平均码长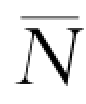 pagenumber_ebook=35,pagenumber_book=29 满足以下条件

离散无记忆信源编码（DMS）

相关推荐