这种变形形式称为轴向拉伸或压缩。图3-30简易吊车图3-31液压传动中的活塞图3-32拉、压杆力学简图2.杆件轴向拉伸与压缩的内力和应力内力构件工作时承受的载荷、自重和约束力,都称为构件上的外力。由于外力F 的作用线沿着杆的轴线,内力FN 的作用线也通过杆的轴线,故在轴向拉伸或压缩时,杆件的内力称为轴力。据此现象可设想,杆件......
2025-09-29
图8-35 所示为计算得到的8.1.2 节中三种不同颗粒体积分数和颗粒分布细观结构模型的应力-应变曲线。由图中可以看出,随着外加载荷的增加,应力随应变逐渐升高,直至达到峰值。具有较高颗粒体积分数的模型一在较小的破坏应变(应力达到峰值的应变)下达到临界破坏应力,并且斜率更陡,说明高颗粒体积分数模型的有效弹性模量大。然而,随着颗粒体积分数的增大,炸药的脆性增加,更容易发生拉伸破坏。对于颗粒体积分数为62%和63%的模型二和模型三,由于黏结剂的增多,增强了炸药承受变形的能力,从而延迟界面断裂。颗粒体积分数对破坏应变有显著影响。模型一、模型二和模型三的破坏应变分别为0.8%、1.3%、1.39%。
从模型二和模型三的应力-应变响应来看,不同的尺寸分布对PBX 的破坏行为也有影响。由图8-35 可以看出,在峰值压力之前,应力-应变响应几乎重合,模型二的临界破坏应力早于模型三,模型三的临界破坏应力高于模型二。可以推测,平均粒径较小的模型三更有利于提高PBX 的力学性能。
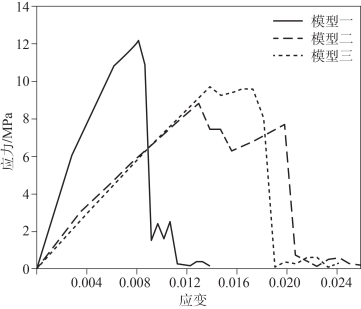
图8-35 三种不同颗粒体积分数和颗粒分布细观结构模型的应力-应变曲线
图8-36~图8-38 所示为三种细观模型在动态拉伸载荷下的损伤破坏过程。对于颗粒体积分数为84%的模型一,在加载初期由于界面的材料强度较弱,观察到界面脱黏,在颗粒/基体界面逐渐出现一些分散的微裂纹[图8-36 (b)]。随着时间的推移,基体和颗粒/基体界面继续受到损伤,微裂纹继续产生;然后产生的微裂纹沿大颗粒边界传播并相互融合[图8-36 (c)];最后,在时间t=27.2 μs 时,形成一个主裂纹[图8-36 (d)]。当主裂纹形成时,其他区域的裂纹也停止了扩展。在模型二中以及在颗粒/基质界面[图8-37 (a)]中观察到微裂纹的出现,而在模型三中尚未产生微裂纹。结果表明,模型二和模型三比模型一需要更多的时间来引发裂纹。在时间t=48 μs 时,模型二中形成主裂纹[图8-37(d)]。当t=33.2 μs 时,模型三开始在颗粒/基体界面上产生微裂纹[图8-38 (a)],并且在t=42.8 μm 时形成主裂纹[图8-38 (d)]。三种模型的破坏演化基本相似,微裂纹总是以分散的方式在颗粒/基体界面萌生,也就是通常所说的界面脱黏。界面脱黏总是在大颗粒边界处首先发生;然后在基体中也产生微裂纹,裂纹沿着大颗粒边界逐渐汇合;最后相互贯通,形成垂直于加载方向的主裂纹,颗粒未发生破坏。通过比较可以发现,颗粒体积分数和分布影响了裂纹的产生和发展,较高的颗粒体积分数降低了相邻颗粒间基体的平均厚度,从而导致更严重的黏结剂变形和界面破坏。从三种模型的计算结果可以发现,动态拉伸作用下PBX 的损伤机理主要是界面脱黏和黏结剂撕裂。

图8-36 模型一的损伤破坏过程(https://www.chuimin.cn)
(a)t=15.2 μm;(b)t=20.4 μm;(c)t=24 μm;(d)t=27.2 μm
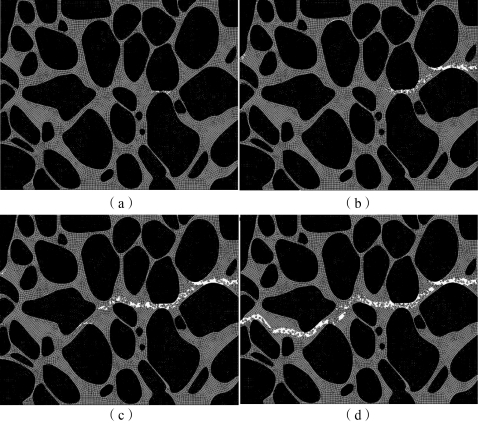
图8-37 模型二的损伤破坏过程
(a)t=27.2 μm;(b)t=41.2 μm;(c)t=47.6 μm;(d)t=48 μm

图8-38 模型三的损伤破坏过程
(a)t=33.2 μm;(b)t=42 μm;(c)t=42.4 μm;(d)t=42.8 μm
相关文章

这种变形形式称为轴向拉伸或压缩。图3-30简易吊车图3-31液压传动中的活塞图3-32拉、压杆力学简图2.杆件轴向拉伸与压缩的内力和应力内力构件工作时承受的载荷、自重和约束力,都称为构件上的外力。由于外力F 的作用线沿着杆的轴线,内力FN 的作用线也通过杆的轴线,故在轴向拉伸或压缩时,杆件的内力称为轴力。据此现象可设想,杆件......
2025-09-29

低碳钢是指含碳量低于0.3%的碳素钢。这类钢材在工程上使用广泛,在拉伸试验中表现出来的力学性能也最为典型。因此首先以低碳钢为例,介绍拉伸试验的方法及低碳钢的力学性能。图4-20 为低碳钢试件的拉伸图。图4-20低碳钢试件的拉伸图1.第Ⅰ阶段 弹性阶段这一阶段可分为两部分:如图4-18 所示,斜直线OA 和微弯曲线AB。直线部分的最高点A 所对应的应力值σp,称为比例极限。......
2025-09-29

由系统的传递函数框图可得EPC系统的开环传递函数为式中 k——开环放大系数,。将算得的ωh、ξh、k代入式,可据此画出EPC系统的开环伯德图。图12-18 改造前后CP机组EPC系统的开环伯德图由图12-18可得系统的性能指标为:①穿越频率:ωc=2.4Hz;②幅值裕量:h=16dB;③相位裕度:γ=75°。可见实测值和理论分析值比较接近,说明上面建立的EPC系统的数学模型和确定的参数是正确的,是可以作为预测改造后系统性能的依据的。......
2025-09-29

黄河下游枯、平、丰水年的水沙资源优化配置模型计算方案与历史实测水沙分布比较如表12-9所示。表12-9黄河下游水沙资源优化配置模型计算方案与历史实测水沙分布比较表对于平水年,1986~1999年实测年平均水沙资源分配主要是工农业引水量111.51亿m3、汛期水量92.50亿m3和非汛期水量58.06亿m3,由于引水含沙量较大,下游引水引沙1.116亿t,河槽淤积2.5亿t,河槽严重萎缩,滩区仅淤积0.395亿t,“二级悬河”迅速发展。......
2025-09-29

把单位面积上内力的大小称为应力,并以此作为衡量受力程度的尺度。截面上的应力可以进行分解,其中垂直于截面的应力为正应力,用字母σ 表示;平行于截面的应力称为切应力,用字母τ 表示。图4-12截面上的应力横截面正应力在国际单位制中,应力的单位是牛/米2,又称帕斯卡,简称帕。为此对杆进行拉伸或压缩实验,观察其变形。求此时斜杆AB 横截面上的正应力。......
2025-09-29

为了验证黏结剂Estane 参数的有效性,首先对黏结剂在应变率分别为0.005 s-1、0.5 s-1和15 s-1的条件下进行了模拟计算,得到黏结剂在不同应变率下的应力-应变曲线,并将计算结果与实验结果[16]进行对比。图7-14黏结剂Estane 数值计算和实验结果比较为了观察黏结剂的黏弹性作用对PBX9501 力学性能的影响,分别模拟了在应变速率为0.001 1 s-1、0.011 s-1、0.11 s-1和0.44 s-1条件下的单轴压缩实验,与实验测量值进行比较。......
2025-09-29

在单闭环有静差调速系统中,引入转速负反馈且有了足够大的放大系数K后,就可以满足系统的稳态性能要求。为此,必须进一步分析系统的动态特性。知道了各环节的传递函数后,按它们在系统中输入、输出的相互关系,可画出图2-15所示的单闭环调速系统的动态结构图。系统开环额定转速降满足静态指标的闭环系统转速降显然,若满足静态性能指标,系统将是不稳定的,说明静态精度与动态稳定性是相互矛盾的。......
2025-09-29

我们设计了4种节能模式和多周期混合自适应休眠方法,并假设两个动态带宽分配周期作为轮询周期。保持接收器的部件功能处于活动状态。在为控制器分配带宽之前,服务器应该检查GATE队列。服务器将数据槽持续时间分配为US和DS缓冲区积压之间的最小值。当将4种节能模式结合到融合网络系统的操作中时,调度方案必须指定将打盹时段和轻/深睡眠时段插入现有数据传输顺序的位置以及GATE消息。图9-15MH-DBA方案操作流程......
2025-09-29
相关推荐