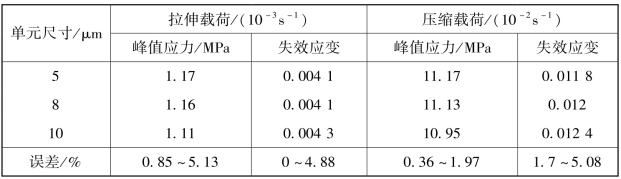
为了保证计算的准静态条件，采用质量缩放时要确保相对于总内能质量缩放产生的动能可以忽略不计，由图8－18 可知加载过程中动能与内能之比小于5%，说明计算是准静态条件。5 μm、8 μm 和10 μm 三种不同的单元尺寸用来分析单元尺寸的影响，计算得到的拉伸应变速率为10－3s－1和压缩应变速率为10－2s－1时的峰值应力和破坏应变如表8－2 所示。峰值应力和破坏应变的相对误差小于5.13%。考虑到效率和精度之间的平衡，选择了8 μm 的单元尺寸进行进一步的模拟。
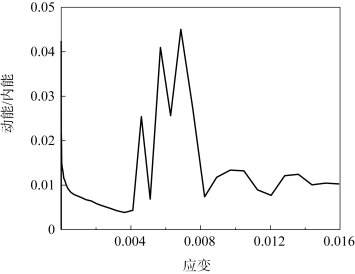
图8－18 动能与内能之比
表8－2 不同单元尺寸下的峰值应力和失效应变
Wu 等［8］和Rangaswamy 等［17］测量得到的PBX 9501 拉伸和压缩应力－应变曲线用于校准不同应变速率下的模拟结果。图8－19 所示为PBX 9501 在10－4s－1、10－3s－1和10－2s－1三种应变速率下实验和模拟获得的应力－应变曲线。在单轴拉伸［图8－19 （a）］和压缩［图8－19 （b）～（d）］下测量和计算的结果相互吻合。在应变速率10－3s－1下计算的拉伸强度、破坏应变和弹性模量约为1.16 MPa、0.004 1 和0.97 GPa，这些值接近于实验获得的1.15 MPa、0.004 2 和1 GPa 的值。在10－4s－1、10－3s－1和10－2s－1三种应变速率下，数值模拟得到的抗压强度分别为8.16 MPa、9.36 MPa 和11.13 MPa，与实验得到的7.97 MPa、9.57 MPa 和11.15 MPa 的抗压强度比较接近。破坏应变分别为0.011 7、0.011 8 和0.012，与实验测得的0.011 7、0.011 9 和0.012 2 的破坏应变比较接近。
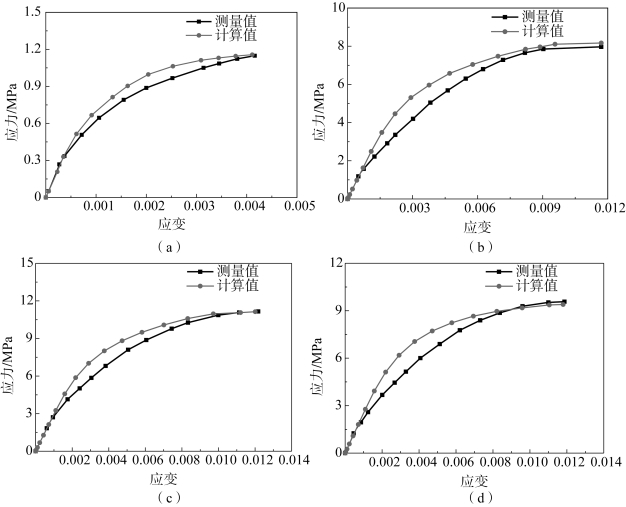
图8－19 测量和计算的应力－应变曲线
（a）拉伸；（b）压缩应变率为10－4s－1；（c）压缩应变率10－3s－1；（d）压缩应变率10－2s－1
有关高聚物黏结炸药损伤断裂的数值模拟的文章
采用对应态热导率模型、Chung法和Stiel-Thodos模型,对二元混合物气体的热导率进行了预测,预测结果与Christensen[27]测得的甲烷-氮气、甲烷-二氧化碳实验数据进行了对比,见表1-18～表1-20。由表中的预测结果可知,对应态热导率模型的平均绝对误差为5.03%,Chung法,Stiel-Thodos模型的平均绝对误差分别为4.93%和7.57%。而且对应态热导率模型的适用温度、压力范围广,可以对天然气的气态、液态热导率进行计算,精度较高,优点较为明显。......
2023-06-24
之后计算求得该组5个制品减重百分数的平均值xi，作为该组实验的结果。表6-9 实验结果表6-10 实验结果表6-11 实验结果表6-9～表6-11中，每一行为一组实验数据，各因素下为对应的水平号。表6-10～表6-11中实验号5、13、14的实验结果明显小于其他数据，后续数据处理中保留了这些数据，没有作为奇异项处理。图6-32 一个注塑周期的实验数据图所有数据统一在一个时间轴下记录，为后续数据分析提供了便利。......
2023-07-02
（一）实验结果与结论表1实验班与对照班各阶段作文专项测试情况统计表说明： ①前测情况，由课题组在新生分班时考试测定，其余各阶段情况由课题组分别在各阶段结束时考试测定。县教研室、学校领导对实验老师予以了充分的理解和支持；实验初期的波折，没有影响实验的继续推行。......
2023-11-22
切削温度计算值与测试值之差相对误差也在5%的允许范围内，见图4-21b。图4-22 车削时切削温度与切削深度、进给量的特征曲面以及切削温度特征曲面等值线图a）切削温度与切削深度、进给量的特征曲面 b）切削温度特征曲面等值线图2.铣削实验结果分析由图4-23a可知，切削温度模型拟合得也较好。......
2023-06-27
本次研究分别通过直接考虑取用水资源的数量与质量以及考虑受益部门取用水的效益等两种方法,对新安江流域上游地区生态保护建设投入在上下游之间进行了分担,分析结果为建立生态共建共享机制提供技术支持。......
2023-11-21
实验结束后回收缩比弹，4 发实验弹的弹体均保持完整。实验前、后分别对缩比弹称重，发现其质量几乎没有变化。对加速度信号进行低通滤波处理，得到弹体刚性加速度曲线。从图5－8 及表中可知，4 组实验由加速度传感器测得的弹体最大过载值与经验公式相比，误差小于10%。射线源至样品的距离为55 mm，成像放大倍数为23.64，体元分辨尺寸为16.92 μm。......
2023-06-27
现将上述成果经综合列入表14.9。表14.10各种树种的截留公式参数表14.11森林实验站典型大洪水对比观测资料表树干流下量。......
2023-08-23
实验中触头预压力FK保持为25.1N。表6-5为两组实验和仿真的详细结果数据。图6-21为峰值电流为11.3kA时的电流和电动斥力实验波形。表6-5 实验和仿真结果比较在仿真中，表征触头接触情况的参数ξ取值为0.45。而电流峰值为9.0和11.3kA时，对应的触头压力分别为35.4和55.9N。根据式（6-1），可得导电斑点的半径分别为0.158和0.199mm。因此，引入导电桥模型，采用有限元静态分析的方法计算电动斥力是合理的，也是有效的。......
2023-06-15
相关推荐