矢量b＋和bα可以表示为2.黏聚应力与软化曲线黏聚裂纹模型主要开裂方式是Ⅰ型裂纹。单元的破坏准则采用最大拉应力的破坏准则，当黏聚应力高于拉伸强度时，开始计算裂纹张开位移。黏聚裂纹模型计算时，裂纹必须沿单元寻找其路径，在这些被选中的单元中，最大主应力至少应超过拉伸强度一次。......
2023-06-27
黏聚界面模型：理论和应用
【摘要】：对于黏聚裂纹模型，认为在真正裂纹尖端前存在着一个假想的区域，通常称为黏聚区，该区裂纹尖端为未损伤和损伤材料的分界点。对于Ⅰ型裂纹黏聚裂纹模型如图8－5 所示。图8－5黏聚裂纹模型基本假设对于黏聚裂纹模型本构，众多学者给出了各种形式的描述，其中双线性黏聚裂纹模型因其适用性和易于实现，越来越受到关注，其描述了黏聚区的黏聚力与裂纹张开位移之间的关系，如图8－6 所示。
对于黏聚裂纹模型，认为在真正裂纹尖端前存在着一个假想的区域，通常称为黏聚区，该区裂纹尖端为未损伤和损伤材料的分界点。假设该虚拟裂纹末端的黏聚力为0，为真正的裂纹尖端，黏聚裂纹面张开过程中，黏聚力从0 逐渐增大。当张开位移达到一定值时，黏聚应力达到最大，然后随着裂纹面张开位移的继续增加，黏聚区内黏聚应力逐渐减小到0。对于Ⅰ型裂纹黏聚裂纹模型如图8－5 所示。
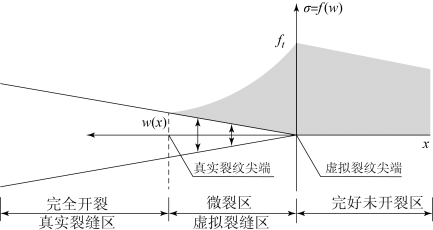
图8－5 黏聚裂纹模型基本假设
对于黏聚裂纹模型本构，众多学者给出了各种形式的描述，其中双线性黏聚裂纹模型因其适用性和易于实现，越来越受到关注，其描述了黏聚区的黏聚力与裂纹张开位移之间的关系，如图8－6 所示。
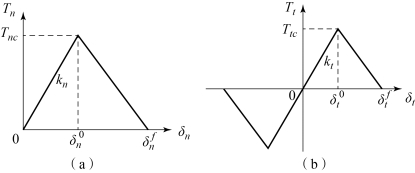
图8－6 双线性黏聚裂纹模型裂纹面黏聚应力与张开位移的关系
（a）Ⅰ型裂纹；（b）Ⅱ、Ⅲ型裂纹
在该模型中，在初始阶段随着张开位移的增加，裂纹表面黏结力将逐渐增加；当张开位移达到一定值时，裂纹面间的黏结力达到最大值；随着裂纹表面间张开位移的继续增加，裂纹面间黏结力将逐渐降低到0，此时裂纹面最终形成。在黏结力达到开裂强度之后，材料表现为线性软化行为，是材料的软化阶段，也称为损伤阶段。其本构关系可以表示为如下形式：
当δn＞0 时，有
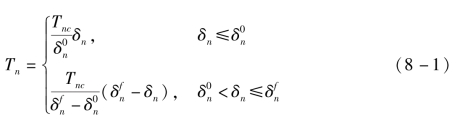
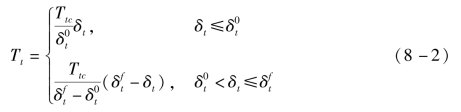
当δn＝0 时，有
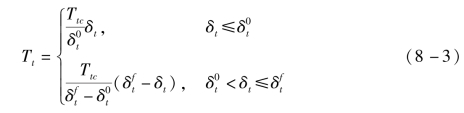
式中：下标n 和t 分别为沿裂面法向和切向的单位矢量分量；δ 为裂面张开位移矢量，δn＝n·δ 和δt＝t·δ 分别为裂面张开位移的法向和切向分量，分别表示黏聚面的最大拉伸强度和剪切强度；
分别为对应于最大拉伸强度和剪切强度的裂面张开位移的法向和切向分量；
分别为黏聚面最大张开位移的法向和切向分量；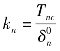
和
分别为法向和切向初始刚度。
作为模拟裂纹破坏的本构关系，其可以分为未损伤、损伤和完全破坏三个阶段。材料进入损伤的节点即损伤起始，目前主要有最大应力准则、最大应变准则、二次应力准则、二次应变准则等破坏起始判定准则。
（1）最大应力准则定义为
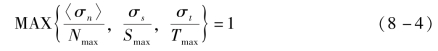
（2）最大应变准则定义为
（3）二次应力准则定义为
（4）二次应变准则定义为
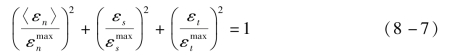
式中：Nmax、Smax和Tmax分别代表当变形是法向（对应Ⅰ型裂纹）、剪切1 方向（对应Ⅱ型裂纹）以及剪切2 方向（对应Ⅲ型裂纹）时应力的峰值，在此即三个方向的最大黏结强度；同样地，
和
分别代表当变形是法向、剪切1 方向以及剪切2 方向时应变的峰值。根据模拟中材料的性质及主要裂纹类型，本章细观模拟采用的损伤起始准则是最大应力准则。
其中，为了防止黏聚面的互嵌而加入了〈〉，即
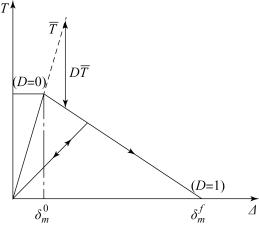
图8－7 损伤演化
损伤起始后，材料就开始损伤演化，损伤演化是指材料出现损伤后，力学性能随着张开位移的增加而逐步退变，其过程如图8－7 所示，可以引入损伤因子D 描述这一过程。其中，D 的取值范围为0～1，当D＝0 时表示材料完好，未发生破坏；当D＝1 时表示材料完全破坏。材料损伤后，其演化刚度为
式中：K0为材料未损伤时的刚度。
由式（8－9）可以看出，材料损伤演化过程的描述关键在于对D 的计算。对于黏聚裂纹模型，不同的黏聚裂纹模型的刚度弱化系数D 通常是不同的，对于双线性黏聚裂纹模型，损伤因子D 可由下式计算：
式中：
为破坏起始时（D＝0 时）单元节点的张开位移量；
为D＝1 时节点的张开位移量；
为在载荷历程中节点的最大张开位移量。
演化过程中所形成的三角形的面积分别代表Ⅰ型、Ⅱ型和Ⅲ型裂纹的断裂能，即GⅠc、GⅡc和GⅢc，可以表示为
黏结界面单元根据所在位置不同可分为三种：颗粒之间、黏结剂之间、颗粒与黏结剂之间的界面上，因此需分别确定三种黏结单元的材料参数。
图8－8 刚度等比弱化
PBX 具有明显的拉压不对称性，拉、压载荷作用下，法向拉应力与切向剪应力对裂纹的起裂分别起到主要作用。由黏结单元的相关实验研究可知，法向和切向方向上的参数通常有所差异，因而黏结单元的损伤起始与临界分离位移的计算与确定将更为复杂。为了简化黏结单元的本构模型，便于参数的确认，对法向与切向刚度做了等比弱化的假设［7］，即dn＝dt＝D，如图8－8 所示。从图8－8 中可以看出，黏结的切向与法向在同一个位移达到损伤起始及完全失效，当切向与法向的位移相同时，二者的刚度总是保持同一个比例。
颗粒间的黏结单元用于描述颗粒内部损伤断裂，由文献［7］得知HMX的拉伸强度可作为炸药晶体黏结单元的法向黏结强度，其值约为4.754 MPa，对应的
。在平面应力状态下，当主应力为
、0 时裂纹萌生，其中
为单轴压缩时的屈服强度，约为260 MPa；
为单轴拉伸时的断裂强度，即4.754 MPa；f＝0.3。计算得到剪应力约为131 MPa，由于压缩载荷下剪应力引起裂纹，因此将剪应力作为黏结单元的切向黏结强度。文献［8］中提出的位移5 μm 用于法向（Ⅰ型裂纹）和切向（Ⅱ型裂纹）的临界分离位移，计算得到法向起始刚度约为2 GPa／μm，切向起始刚度约为55 GPa／μm。图8－9 所示为HMX 晶体拉伸应变速率10－3s－1时计算和测量的应力－应变曲线。利用文献中的参数可以准确地表征HMX 晶体的力学行为。
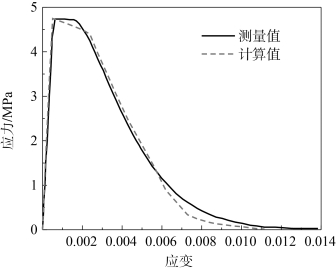
图8－9 HMX 晶体拉伸应变率为10－3s－1时计算和测量的应力－应变曲线
对于黏结剂之间的黏结单元，结合文献［8，9］中的数据，取值如下：法向和切向黏结强度分别为5 MPa 和38.4 MPa，法向切向初始刚度分别为1 GPa／μm 和7.68 GPa／μm，临界分离位移为5 mm。图8－10 所示为拉伸应变率为10－3s－1时计算和测量得到Estane 5703 的应力－应变曲线。计算结果和实验结果吻合较好。
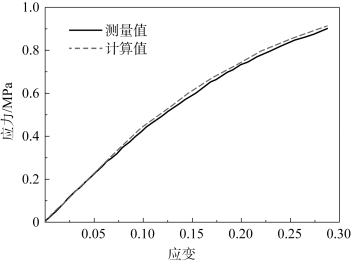
图8－10 拉伸应变速率为10－3s－1时计算和测量得到Estane 5703 的应力－应变曲线
颗粒／黏结剂界面黏结单元用来描述PBX 界面脱黏及剪切破坏，Tan等［11］结合数值图像相关方法和紧凑拉伸实验，对PBX 9501 的脱黏过程进行了研究。用数字图像相关方法得到紧凑拉伸实验中宏观裂纹尖端的应力和位移场，进而利用考虑界面损伤效应的Mori－Tanaka 方法，将宏观实验数据与细观的界面脱黏联系起来，提出了如图8－11 所示的三阶段界面脱黏细观损伤模型。三阶段依次为阶段Ⅰ（上升段）、阶段Ⅱ（软化段）和阶段Ⅲ（完成脱黏段）。三个阶段中界面上的法向拉应力与张开位移的关系如下：
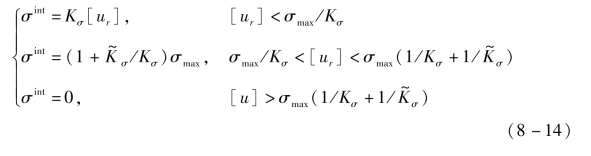
图8－11 三阶段界面脱黏模型
本节将颗粒／黏结剂界面脱黏等同于PBX 9501 的界面脱黏，模型包含的三个参数：线性模量为初始刚度kn＝1.55 GPa／μm，黏结强度Tnc＝1.66 MPa，临界分离位移
。
对于颗粒／黏结剂界面的Ⅱ型裂纹，实验表明其断裂模式主要伴随着黏结剂的撕裂。根据Dienes 和Kershneer［12］的实验数据可知，PBX 9501 黏结剂撕裂过程中，单位面积消耗的能量约为195 J／m2。利用等比刚度弱化假设及式（8－12）计算得到界面黏结单元的切向黏结强度约为3.55 MP，初始刚度为3.3 GPa／μm。
PBX 9501 是率相关材料，究其原因，除了黏结剂本身的黏弹性外，黏结强度也随加载速率发生相应的变化。Wu 等［8］根据不同应变率条件下实验所得界面脱黏的断裂能，获得界面张开位移和拉应力的关系，如图8－12 所示。黏结强度和断裂能随应变速率的增加而增加，因此模型中通过考虑不同应变速率下的界面参数来实现界面的应变速率效应。表8－1 列出了三种界面单元的模型参数。炸药和黏结剂模型及参数见第7 章。
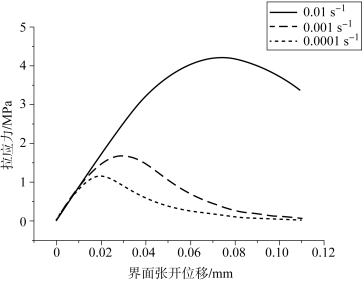
图8－12 不同应变速率下界面张开位移和拉应力的关系
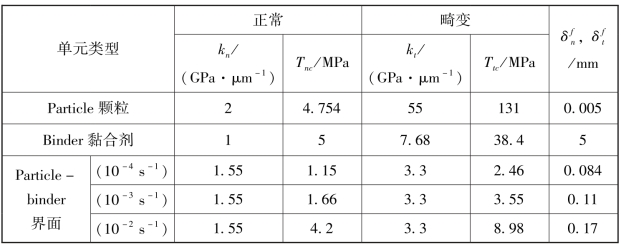
表8－1 各界面黏结单元材料参数
如文献［12～14］所述，由于在原本完整的模型中插入了含有初始刚度的黏聚界面单元会导致材料刚度降低，计算时需要采用一个足够大的刚度系数和相对小的网格尺寸来避免这个问题。
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
聚能射流侵彻的理论探究详细阅读
图1.26聚能射流典型破甲过程示意基于上述假设，将坐标原点设置于射流与靶板接触点A，以点A为观察点，射流和靶板材料分别以速度vj-u和速度u运动。以上原因均表明，射流断裂后，侵彻能力将大幅下降。图1.28断裂射流侵彻模型设断裂时射流头部速度为vjB，经过时间t，长度l的断裂射流消耗完毕，侵彻深度为L，速度为vj的点A射流到达孔底D。......
2023-06-18
-
应急设施布局优化理论与应用：原有模型详细阅读
应对大规模应急服务需求的SHSCP模型是在所有网络节点集合中，选择一定数量的节点作为枢纽点，将其余的非枢纽点分配给枢纽点，满足所有约束下，使枢纽数量最少。模型中参数假设如下。例如在应急救援过程中，规定所有的应急救援队伍必须在24小时内到达应急现场并开展救援工作，此时T=24小时。......
2023-09-19
-
聚能射流成形的理论探究详细阅读
图1.13射流成形定常流动模型建立射流成形的定常流体力学理论，所作假设如下：爆轰波到达药型罩表面，微元以大小和方向不变的压合速度运动；各微元速度v0及变形角δ相等；变形过程中罩长度不变，即AC=BC。......
2023-06-18
-
界面反应系数的原子模型优化方案详细阅读
在3.2.4节的动力学分析中，最重要的两个动力学参数是原子扩散率和界面反应控制系数。为了方便比较，在界面反应控制系数中我们提出了一个类似的表达式。图3.11描述了越过Cu6Sn5/Sn界面的活化能，其中ΔGm是穿过界面的迁移活化能，ΔG是反应中或者是Cu6Sn5生长中每一个原子对应的化合物的自由能增益（驱动力），而λ是界面的宽度。图3.11越过Cu6Sn5/Sn界面的活化能式中，p为压力。但由于界面反应过程极其缓慢，因此不太可能考虑分子生长。......
2023-06-20
-
STAR-CCM+用户界面和功能详解详细阅读
图2-40 STAR-CCM+用户界面图2-41 File菜单图2-42 Edit菜单图2-43 Mesh菜单图2-44 Solution菜单图2-45 Tools菜单图2-46 Window菜单STAR-CCM+的用户界面非常友好，操作简单。图2-47 Help菜单通过Solution菜单可以实现计算条件初始化、开始计算、停止计算等功能，并可以清除历史计算记录。通过Tools菜单可以选择、取消和定制软件界面上显示的工具，包括工具栏工具。图2-48 启动TCM模块通过Window菜单可以控制和调整视图区的显示方式。通过Help菜单可以查询帮助文件和检索疑难问题。......
2023-10-17
-
基于高斯混合模型的聚类算法：期望最大化详细阅读
图9－4K－Means不适用的情况高斯混合模型具有比K－Means更好的灵活性。使用GMM，需要假设数据点是高斯分布，相对于环形的数据而言，这个假设的严格程度与均值相比弱很多。因此，每个高斯分布会被分配到单一的聚类簇。基于这些概率，我们为高斯分布计算了一组新的参数，这样就可以最大化集群中数据点的概率。......
2023-06-21
-
类射流活性聚能侵彻体释能模型探析详细阅读
与此同时，活性聚能侵彻体后部杵体形成，变形过程中温度继续升高，由于未到达激活弛豫时间，未发生反应。图3.2类射流活性聚能侵彻体化学能分布式释放计算模型根据类射流活性聚能侵彻体的形状，其可分为头部、中部及杵体3部分。式即类射流活性聚能侵彻体化学能随时间分布释放模型。在空间尺度上，类射流活性聚能侵彻体不断拉伸、运动。......
2023-06-18
相关推荐